一道高考立幾選擇題的多解剖析

江西省臨川二中 (344100)

黃衛民

2018全國一卷理科第12題：

已知正方體的棱長為1，每條棱所在直線與平面α所成的角都相等，則α截此正方體所得截面面積的最大值為( ).

分析：這道題是出自必修2的研究性課題正方體中有關截面問題的改編題,本題以學生最為熟悉的正方體為背景，求與正方體棱所成角相等的截面面積的最大值，解決本題的幾個關鍵環節分別是：確定截面的方向和形狀，明確截面面積何時取得最大值，最后求出最大值.

解法一：因為一組平行線與已知平面所成的角都相等，而正方體有12條棱，共構成三組平行線，故每條棱與截面所成的角可化歸為同一頂點出發的三條棱與截面所成角.根據經驗能直觀感知到平面AB′D′是符合要求的平面(圖1)，由對稱性可知，平面BDC′也是符合要求的平面(圖2)，且與平面AB′D′平行的平面都與這三條直線所成角相等.

根據以上分析，易知該截面的形狀為：由小變大的正三角形——六邊形——正六邊形——六邊形——由大到小的正三角形.根據基本活動經驗學生可以判斷(或猜想)出當截面形狀為正六邊形時，截面面積應該最大(圖3).

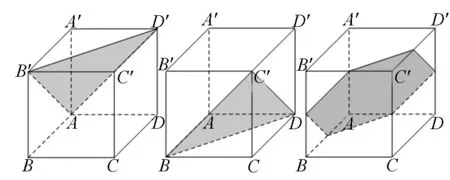
圖1 圖2 圖3

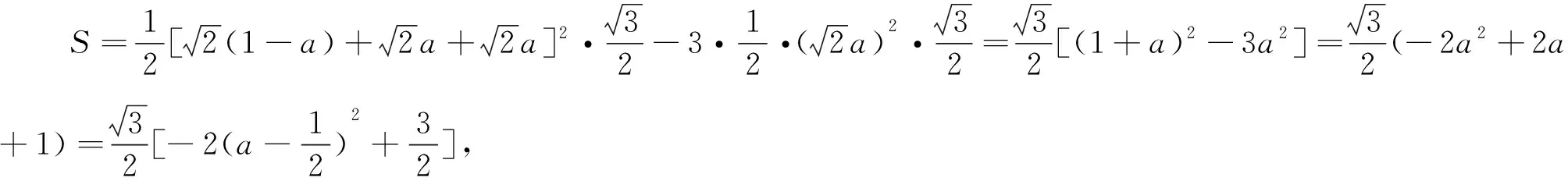
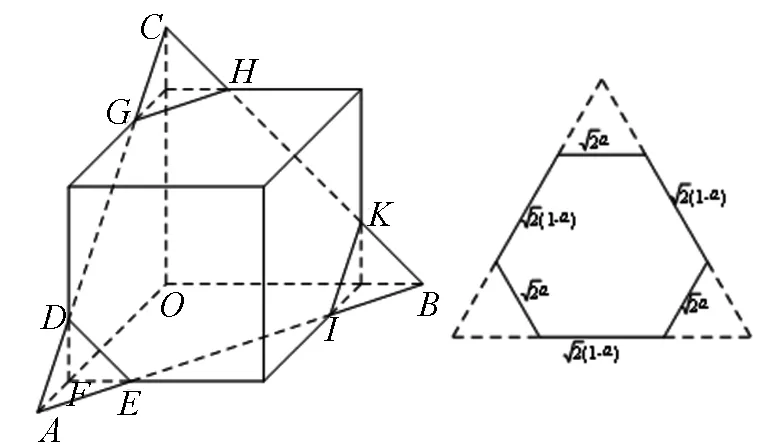
圖4 圖5

點評：解法二的計算對截面形狀的判斷要求很高，尤其是截面六邊形在正三角形內學生不易想到，可考慮將截面積的計算問題轉化為投影面的計算，將問題簡化，于是有解法三.

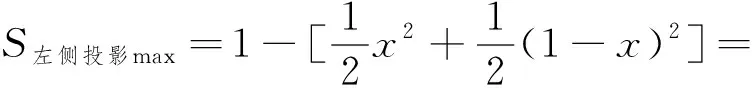
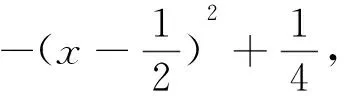
對于空間感不強，空間位置判斷不好的同學，也可以考慮用空間坐標系來尋找解決方法.

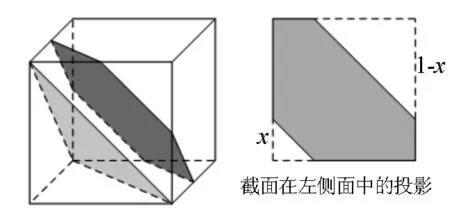
圖6

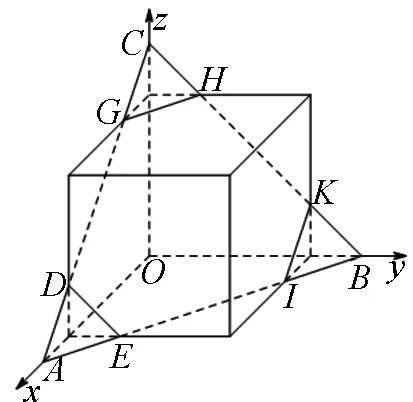
圖7

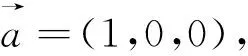
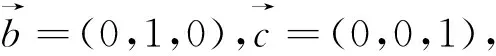
結語：本題以正方體為背景，通過求與正方體棱所成的角相等的截面面積的最大值這一問題，綜合考察了學生分析問題、數學抽象、猜想論證、數學建模、函數最值的求法等多種知識和能力.