問題導向，關注過程，引領思維，啟迪智慧
——提高初中數學例題教學有效性的探索與思考

☉江蘇省張家港市塘市初級中學 朱 薇

例題是把知識、技能、思想和方法聯系起來的一條紐帶，知識的價值、技能的操作、思想與方法的滲透都要通過例題來體現.例題的選擇非常重要，作為一個靜態的“媒介”，要具備良好的知識性、示范性和發展性.好的例題，不僅可以幫助學生加深對定義、定理、概念、法則的理解，培養學生的解題技能、積累解題經驗，而且可以加強學生的思維訓練，提高學生分析問題和解決問題的能力.例題的講解與示范是教學中傳授知識、培養技能必不可少的一個環節，是學生理解、掌握數學知識，運用數學知識解決問題的必要過程，是學生將數學知識和技能轉化為能力的必要途徑.因此，例題教學是數學課堂教學的重要組成部分，肩負著把知識轉化為能力的重要使命，其質量的高低直接影響學生對數學知識的掌握.科學、合理地選擇數學例題，并在教學過程中，讓學生獲得系統的數學知識，形成必要的解題技能，是數學備課過程中一項十分重要的工作，是一個教師教學智慧和藝術的重要體現.下面就本人執教的“三角形的中位線”一課的例題教學環節，談一些例題教學的做法與感悟.

一、設置理解知識的基礎訓練問題，夯實“雙基”，有效進行知識同化，體現例題教學的示范功能

認知心理學認為，新知識的學習必須建立在舊知識的基礎上，當學習者的認知結構中形成了新的概念、學習了新的知識以后，新知識和舊知識必須予以同化，這樣不僅能夠幫助學習者學習新知識，而且可以幫助其保持知識.數學概念、知識、方法都需要通過例題加以鞏固，選擇合適的例題對于課堂教學來說是非常重要的.正確發揮例題的示范功能，能使學生的思維能力、解題能力得到很好的鍛煉，從而能從容地面對以后學習中所遇到的各種數學問題.因此，例題的難度必須要控制好，能說明問題、起到示范作用就行.在“三角形的中位線”一課的教學中，我設置了如下一組簡單的基礎問題，引導學生正確、合理地應用三角形的中位線定理解決數學問題，加強新知識和舊知識之間的聯系.

例1（1）如圖1，在△ABC中，已知D、E分別為邊AB、AC的中點，連接DE，若∠C=70°，DE=3cm，則∠AED=______°，BC=______cm.

（2）如圖2，在△ABC中，已知D、E、F分別為邊AB、AC、BC的中點，連接DE、EF、DF.

①圖中共有幾個平行四邊形？

②若△ABC的面積為8，則△DEF的面積為______.

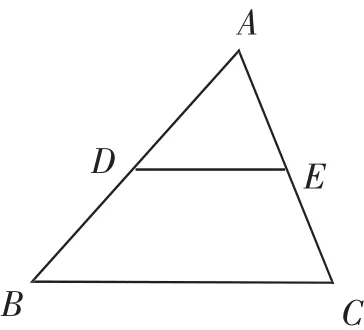
圖1

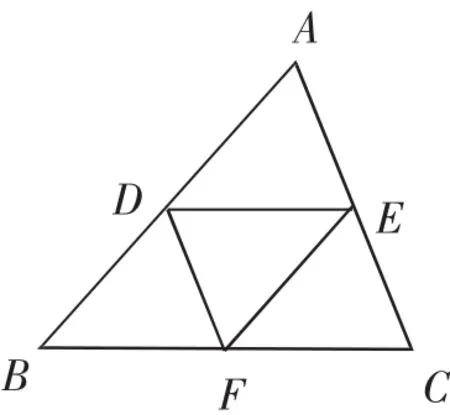
圖2

在幾何例題教學中，教師要不斷引導學生讀圖、識圖、分析圖形，學會從圖形中捕捉信息、加工信息、尋找到解決問題的關鍵點，同時要引導學生及時進行歸納、總結，積累數學活動經驗和解題經驗.只有這樣，才能充分體現學生的主體地位、教師的主導作用.在本例中，通過問題（1）的訓練，讓學生進一步熟悉定理、感知定理的簡單應用，理清定理的條件、結論之間的關系和定理適用的范圍；通過問題（2）的解答和教師的追問，讓學生能進一步發現：①一個三角形有三條中位線，②三角形的三條中位線將三角形分成四個全等的三角形，其中還蘊含著三個平行四邊形.通過例題的示范，我們要力爭做到：第一，能夠將學生的注意力集中在新知識的重點部分；第二，突出強調新知識與已有知識的關系，為新知識提供一種框架；第三，能夠幫助學生回憶起與新知識相關的已有知識，以便更好地建立聯系.

二、設置鞏固知識的簡單應用問題，啟思明理，有效實現知識內化，突出例題教學的知識功能

例題教學的知識功能指的是通過例題教學使學生獲得系統的數學基礎知識，形成必要的技能.數學思維過程也就是不斷地提出問題和解決問題的過程.因此，教師不但要精心挑選例題，使其具有典型性、層次性和示范性，更要善于對例題加以剖析、變式，必要時還可以適當地將例題進行拓寬、延伸，促進學生對概念的內涵與外延的理解，通過充分的外化過程，實現數學知識的內化，充分發揮例題的知識功能，使其真正達到既落實“雙基”，又培養能力的教學效果.為此，我設置了如下例題：

例2如圖3，已知AF是△ABC的中線，DE是中位線，DE、AF交于G，若AF=5，則GF=______.

教材是重要知識點的精華與濃縮，往往言簡意賅，或者限于篇幅，有些知識、方法未能加以闡釋，常常出現在練習、習題之中，教師作為教材與學生之間的協調者，有必要對簡約的內容進行補充與拓展，加強前后知識的聯系，及時滲透數學思想方法.本例是例1問題（2）的應用與深化，連接DF、EF，四邊形DAEF是平行四邊形，因此，DE與AF互相平分，問題的結果自然顯現.同時，我們可以告訴學生：三角形的中位線與第三邊上的中線互相平分.通過例題的講解與思辯，不僅可以幫助學生加深對知識的理解，培養學生的解題技巧，還可以讓學生啟思明理，拓寬視野，有效實現知識內化，突出例題教學的知識功能.

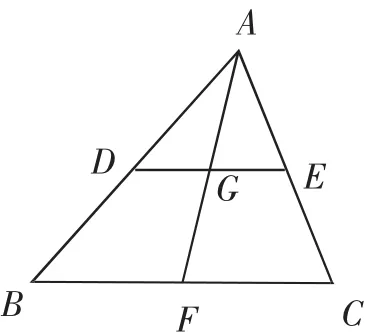
圖3

三、設置拓寬知識的變式訓練問題，引領思維，有效積累活動經驗，凸顯例題教學的教育功能

例題教學的教育功能指的是對學生文化素質的培養，其中重要的是培養學生的思維品質.由于數學問題是數學思維的動力，數學思維過程也就是不斷地提出問題和解決問題的過程.因此，在例題教學中，教師不但要精心挑選例題，使其具有知識性、典型性、層次性和示范性，更要善于對例題加以變式，讓學生在全面、深刻地理解和掌握知識的同時，思維品質也得到相應的提升.幾何教學中，教師更應該做好例題變式教學，為此，我給出了如下問題：

例3如圖4，在△ABC中，已知D、E、F分別為邊AB、BC、AC的中點，G、H分別為AD、AF的中點.若△AGH的周長為m，求△BDE的周長.

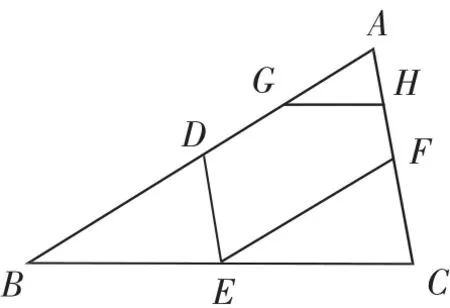
圖4

例3是例1第（2）問的變式，如果連接DF，就會出現例1（2）的圖形，利用三角形中位線定理，我們知道：若△AGH的周長為m，那么，△ADF的周長為2m；利用四邊形ADEF和四邊形BEFD都是平行四邊形，那么，△BDE的周長=△FDE的周長=△ADF的周長=2m.通過這樣的教與學，學生對圖形的認識會更加清晰，對知識的理解會更加深刻，對解題方法的掌握會更加牢固，對幾何推理的書寫會更加熟悉、規范.變式既是一種重要的思想方法，又是一種行之有效的教學方式.通過變式教學，有利于培養學生研究問題、探索問題的能力，幫助學生積累探究活動的經驗，是思維訓練和能力培養的重要途徑.

四、設置深化知識的綜合應用問題，啟迪智慧，有效提升關鍵能力，彰顯例題教學的拓展功能

《義務教育數學課程標準（2011年版）》指出：“數學課程應致力于實現義務教育階段的培養目標，要面向全體學生，適應學生個性發展的需要.使得：人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展.”因此，當學生對知識和技能初步理解與掌握后，教師應當設置一些深化知識的綜合應用問題，加強前后知識的聯系，讓學生進一步鞏固所學知識，消化吸收知識.例題教學中，例題拓展得恰當、設計得巧妙，對于提高課堂教學效率，優化課堂教學結構，往往能起到畫龍點睛的作用，也能為不同的學生留下個性化的發展機會，讓學有余力的學生有更大的發展空間.強化拓展問題的講解與思辯，目的是幫助學生把所學的知識融會貫通，在知識的深化中領略數學的魅力，體會學習數學的樂趣，啟迪智慧，提升關鍵能力，彰顯例題教學的拓展功能.在本課例題教學的最后一個環節，我出示了下面一題：

例4如圖5，在四邊形ABCD中，E、F、G、H分別是AB、BC、CD、DA的中點.

（1）求證：四邊形EFGH是平行四邊形：

（2）若四邊形ABCD的對角線相等，那么四邊形EFGH是什么圖形？

（3）若四邊形EFGH是正方形，那么四邊形ABCD應滿足什么條件？

本例的第（1）問是課本例題，連接對角線BD或AC，利用三角形中位線定理很容易加以證明，主要是引導學生學會構造圖形、合理使用定理.第（2）問和第（3）問結合四邊形的相關知識，對問題進行了適度的拓寬引申，將三角形中位線的知識與四邊形的判定與性質進行了很好的銜接，讓學生對三角形中位線定理的應用有了一個更加深刻的認識.蘇聯教育家烏申斯基指出“智慧不是別的，而是組織良好的知識體系”.通過這樣的數學探究活動，數學知識之間能有機聯系起來，學生的頭腦中才會建立起一個完整的認知結構，逐步形成一個完整的知識網絡，這樣的例題教學才能扎實、有效.

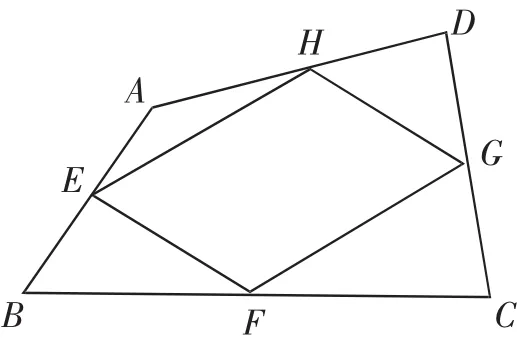
圖5

實踐證明，加強和改進數學例題的教學，對理解和掌握基礎知識、培養數學思維、發展智力都是至關重要的.因此，我們在例題教學中，一方面，要充分利用好教材上的例題，教材中例題都是經過多次篩選編制而成的；另一方面，我們要適當選擇一些課外資料上的問題，作為教材例題的補充與延伸.還要配備好相應的學生練習，讓學生在動手實踐中學會應用例題知識，使得例題與習題緊密聯系在一起，讓例題的教學功能得到充分發揮、起到應有的作用，引領學生的思維，啟迪學生的智慧.