對計算教學中算法多樣化的思考

吳智

[摘要]對算法多樣化的理解不到位、不透徹，沒有很好地把握算法多樣化的核心，是很多教師的教學認識誤區。教師應走出誤區，通過多樣化計算方法給予學生更多的思考空間，促進學生多角度思考問題，加深學生對算式意義的理解，使學生能從中優選出最適合的計算方法，從而快速解決問題，提升解決問題的能力。

[關鍵詞]計算教學;算法;多樣化

[中圖分類號]

G623.5

[文獻標識碼]A

[文章編號] 1007-9068（ 2019）35-0053-02

《義務教育數學課程標準》明確指出：由于學生的生活背景和思考角度不同，所使用的方法必然是多樣的，教師應尊重學生的想法，鼓勵學生獨立思考，提倡計算方法多樣化。算法多樣化是實現學生在數學上得到不同發展的有效途徑，也是尊重學生個性化學習，促進學生個性化發展的有效途徑。可是，很多教師對算法多樣化的理解不到位、不透徹，沒能很好地把握算法多樣化的核心，因此產生種種誤區。下面筆者結合案例對一些誤區加以分析。

誤區一：教學目標不清不楚

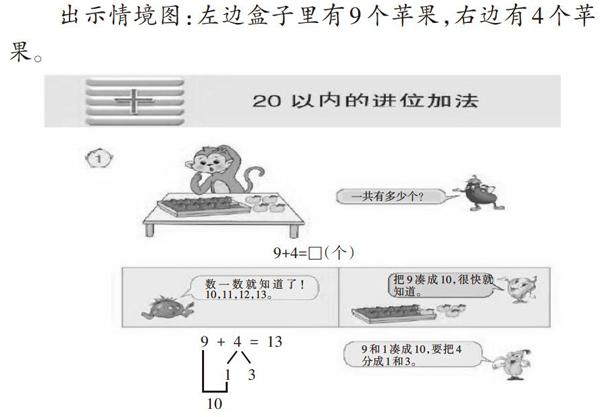
【案例1】蘇教版教材一年級上冊“9加幾”教學片段。

出示情境圖：左邊盒子里有9個蘋果，右邊有4個蘋果。

師：看圖后你能提出什么數學問題？

生1：左邊盒子比右邊盒子多多少個蘋果？

師：誰來回答這個問題？

生2：9-4=5，左邊盒子比右邊盒子多5個蘋果。

師：“9-4=5”，這可是我們前面學習的知識。

生3：左邊和右邊盒子一共有多少個蘋果？

師：這個問題誰能回答？

生4：9+4=13，左邊和右邊盒子一共有13個蘋果。

師：對于“9+4”，你能想出哪些方法來計算？比一比，看誰的算法多。（經過思考后，學生爭著發言）

生5：數一數小棒就知道了，一共可數出13根。

生6：我用9+1=10，10+3=13。

生7：我想到了兩種方法，一種用5+5=10，10+3=13;另一種先數9根小棒，再拿4根小棒，數一數共13根。

生8：我想到了四種方法，第一種用9+1=10，10+3=13;第二種用9+2=11，11+2=13;第三種用9+3=12，12+1=13;第四種用9+1+1+1+1=13。

思考：算法多樣化是基于傳統計算教學“計算方法單一，過于注重技能的發展，忽視學生的個性化發展”等問題提出來的，主要著眼于讓學生經歷探索計算方法的過程，體驗算法的多樣化。可是，在教師“比一比，看誰的算法多”的“煽動”下，學生想到了一種、兩種、三種、四種方法。從中不難看出，學生的這些算法中有些是雷同的，如生。的第二種、第三種方法，都是把4隨意拆分成兩個數來計算;有的學生思維還降低了，如生3、生4的解答方法，生3從湊十法（隨意的）走向數數，生4從最基本、最關鍵的湊十法走向隨意地加。這樣的教學，背離了算法多樣化的目的。教師應該認真領會，準確把握算法多樣化的內涵：算法多樣化并不是追求數量上的“多”，尤其在課堂教學中出現的同一個思維層次的算法，教師不能一概叫好，要觀察判斷學生思維水平是否有質的提升。

誤區二：忽略教師的主導作用

【案例2】蘇教版教材三年級下冊的“兩位數乘兩位數”教學片段。

出示情境圖，引出數學問題：

待學生嘗試計算24x12的積后，組織全班學生交流：

生1：我用豎式計算的（豎式略），先用第二個因數個位上的2乘24，再用十位上的1乘24，最后把兩次相乘得到的積加起來。

生，： 24x12=24x10+24x2=240+48=288.

生3： 24x12=24x2x6=48x6=288。

生4. 24x12=24x3x4=72x4=288。

生5： 24x12=12x4x6=48x6=288。

生6： 24x12=12x3x8=36x8。

師：你們都想到了不同的算法，在這些算法中，你最喜歡哪一種？

生1：我喜歡我想出的列豎式的方法。

生2：我喜歡我想出的第二種算法。

生3：我喜歡我想出的第三種算法。

師：今天學習的主要是列豎式計算，我們一起來回顧列豎式的算法。請大家用列豎式的方法試著做下面的幾道題。

思考：有效引領——讓學生擇善而從之“我喜歡我的算法”，凸顯了教師在算法多樣化中主導作用的缺失。眾所周知，兩位數乘兩位數是在學生掌握兩位數和三位數乘一位數的計算方法的基礎上研究學習的。當出現了多種算法以后，教師應及時組織學生展開交流比較，并將這些算法進行分類。生1和生2的算法本質上是同一類算法，用第二個因數的個位和十位上的數分別乘另一個因數，再將乘得的積相加，只不過呈現的方式不同;其他的算法都是將“兩位數乘兩位數”轉化為“兩位數乘一位數”，轉化為已學過的知識，也應該歸為一類。為了突出列豎式算法的普遍適用性和對后續知識學習的價值，教師要引導學生認識到將“兩位數乘兩位數”轉化為“兩位數乘一位數”這種算法的局限性。其實，教材情境圖的設計也有這層意思，其滲透并不是所有的“兩位數乘兩位數”都可以轉化為“兩位數乘一位數”來計算。例如，在讓學生嘗試計算“29x17”時，學生會選用列豎式的算法，因為沒有辦法將它轉化為“兩位數乘一位數”來計算，這就突出了“兩位數乘兩位數”轉化為“兩位數乘一位數”的局限性，學生就能在選擇算法的過程中感受到列豎式計算是普遍適用的算法。這樣一來，學生就自然而然地把學習重心轉移到研究“兩位數乘兩位數”的豎式計算上。

誤區三：不理解教材編寫意圖

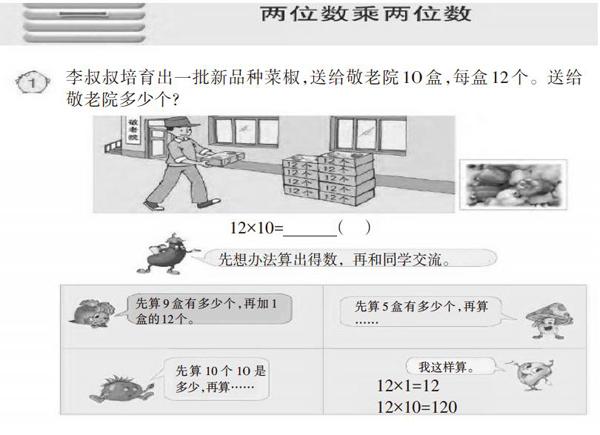
【案例3】蘇教版教材三年級下冊的“兩位數乘整十數”教學片段。

出示情境圖，引出數學問題：

師：怎樣解答？

（學生思考交流，很快得到了結果）

生1：一共10盒，每盒12個，用12xl0，因為12x1=12，所以12x10=120（個）。

師：還有別的算法嗎？

（學生眉頭緊皺，面有難色）

師：動腦筋想一想，還有別的算法嗎？

（教室里一片沉寂）

思考：“兩位數乘整十數”是在學生學習了“兩位數乘一位數”“整十數乘一位數”和“三位數加兩位數”的基礎上學習的。為什么在教師的追問“還有別的算法嗎”下卻沒有出現多樣化的算法呢？教師首先要深思，學生想不出的原因是什么，是否已經給了學生足夠的探索時間，還是學生的探索能力有限，教師是否已經積極引導學生去觀察、去思考、去探究了。其實造成這種情況的主要原因是直接呈現的情境圖沒有激活學生已有的知識經驗，學生不懂觀察情境圖，不知道情境圖的編排意圖，學生更沒有把新的計算問題與已學過的計算方法聯結起來，造成了“無奈追問下，不見期待的精彩”。

其實，教材呈現了四種算法：第一種，先算9盒多少個，再加1盒的12個，用12x9=108. 108+12=120;第二種，先算5盒有多少個，再算10盒有多少個，用12x5=60，60x2=120;第三種，把12拆分成10和2，10個10是100個，10個2是20個，用100+20=120個;第四種，用12xl=12，12x10=120。仔細觀察情境圖，其實第一種算法和第二種算法都是受限于情境圖因素的影響，必須認真細致觀察情境圖，再聯系已經學過的兩位數乘一位數的計算方法，分兩步算出結果。不同的是，從情境圖中得出，第一種算法先算9盒，再加1盒，合起來就是10盒;第二種是先算右邊的5盒，再算2個5盒也就是10盒。如果脫離了情境圖，以上的兩種解答方法很難實現。而第三種算法是把每盒12個拆分成10個和2個，分別算出10個10和10個2，再相加得出120個。第四種算法也是聯系已學過的兩位數乘一位數的計算方法進行類推，因為12xl得12個一，所以12xl0得12個十，12個十也就是120。雖然教材給出的四種算法思路不同，但都是基于學生已有知識經驗的，目的就是讓學生在不同算法中進行交流，在感受不同算法的特點上尋求更適合自己的算法，從而推導出“兩位數乘整十數”的口算方法。

現在教材提供的數學計算方法多種多樣，對于一些方法，有的學生能夠想到，有的學生卻不能，那么教師就應該思考其中的原因：是學生的學習習慣不夠好，還是他們缺乏探索精神呢？發現問題后再一一針對性地去引導學生學習。多樣化計算方法給予學生更多的思考空間，有利于學生多角度思考問題，通過多樣化算法也可以加深學生對算式意義的理解，學生也學會在這個過程中選出最適合自己的計算方法，從而快速解決問題。可見，幫助學生形成解決問題的策略和能力，是促進學生長遠發展的根本方法。

（責編黃春香）