橢圓中的切線方程及其應用

浙江省諸暨市第二高級中學 (311800)

朱水英

切線問題是高中數學的常見問題，如何求切線方程則是解決問題的關鍵.函數的切線方程一般采用導數的幾何意義求解，而圓錐曲線的切線方程一般采用直線與圓錐曲線方程組聯立，消x或y，得到一個一元二次方程，直線與圓錐曲線相切，即方程只有一個實數解，利用判別式Δ=0求解，即判別式法，這也是圓錐曲線中求切線方程的通法，但是此法計算量較大.

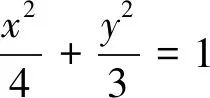
此法就是判別式法的運用，但是計算較大，對很多學生來說可能會出現一種普遍現象：會做但算不對.下面介紹橢圓的切線方程，首先引導學生從導數角度入手自己動手推導橢圓在其上一點處的切線方程.

一、推導切線方程

圖1

圖2

評注：此法是運用了導數的幾何意義進行推導，當然也能用判別式法，但是計算量較大，本文就不做介紹了.對公式推導是為了讓學生在運用公式前能知其所以然，運用已有的導數知識來解決圓錐曲線問題，看似兩塊不同的章節，但也能有相通的地方，能讓學生感知數學知識的相互關聯性，在以后的學習中能開闊思路，提升學習能力.

二、強化切線應用

圖3

分析：此題考查直線與圓錐曲線的位置關系，只有一個公共點即直線與橢圓相切，一般采用判別式法，參考答案也是采用此法，但是計算量大，尤其是帶有三個字母，正確率就更低了，而且還影響了下一小題的解答，因此當年此題的得分比較低.

以下運用橢圓的切線方程解答：

圖4

三、推廣曲線切線

圓錐曲線教學中，橢圓、雙曲線、拋物線有類似的解題思路，是否在切線方程求解上有類似的公式？作為一名高中數學教師不僅要教會學生如何解題，更要教會學生解題的思想方法，這樣才能讓學生舉一反三，提高學習的效率.自己動手，豐衣足食.

(2)點P(x0,y0)為拋物線C:x2=2py上任意一點，則拋物線C在點P之處的切線方程為x0x=p(y0+y).

(3)點P(x0,y0)為拋物線C:y2=2px上任意一點，則拋物線C在點P之處的切線方程為y0x=p(x0+x).

(4)點P(x0,y0)為圓C:x2+y2=r2上任意一點，則圓C在點P之處的切線方程為x0x+y0y=r2.

數學注重對學生核心素養的培養，這是學生受用一生的能力.推理和運算是思維訓練的載體，邏輯推理和數學運算都是中學數學的核心素養，能對所學的知識學以致用，推理出一個新的結論，這也是一種能力的體現.就如本文用導數的思想推導了圓錐曲線的切線方程，就是讓學生體會函數思想是高中數學的基本思想，數學內容是相互串聯的，它們是自成一體的.而數學運算能力是思維能力和運算能力的結合，高考對運算求解能力的考察重點放在算理的應用、運算途徑的判斷、運算方法的選擇上，這也是考察學生的綜合能力，所以在解析幾何教學中，運用一些必要的結論與公式來簡化運算，提升學生解題的信心，是很有必要的一種手段.增強求簡意識，也是我們數學教學和高考復習中必須遵循的.