初中數學教材中“生活情境”的解讀之道*

☉江蘇省無錫市新吳區教師發展中心 浦敘德

隨著數學學科核心素養目標寫進普通高中數學課程標準，相信不遠的將來，它也會進入義務教育數學課程標準.指向數學學科核心素養的教學總是根據數學的本質，創設匹配的教學情境，提出恰當的數學問題，啟發學生的思考，通過情境的“數學化”獲得數學知識，并形成和發展數學學科核心素養［1］.課程內容的結構化與課程內容的情境化，可以促進數學學科核心素養的落實［2］.可以斷定，關于情境的研究依然會是今后一段時間內數學研究的熱門話題.初中數學課堂教學中選取的情境一般有數學情境與生活情境兩類［3］.因為數學情境來自數學內部，體現知識之間的前后結構關聯，所以對數學教師而言是顯性的.課堂實踐表明，教師對數學情境的解讀比較到位.而生活情境來自數學外部的生活實際，體現的是生活中隱含的數學，所以對數學教師而言是隱性的.課堂教學表明，教師對生活情境的解讀還是非常欠缺的，要么當花瓶擺設，很快滑過，要么抓旁枝末節，不達本質.所以非常有必要對生活情境的解讀做一番研究.下面以蘇科版九下“第7章銳角三角函數7.1正切”的生活情境為例，說明初中數學教材中生活情境的解讀之道.

一、數學教材中的生活情境

如圖1，某體育館為了方便觀眾，設計了不同坡度的臺階.

1.在圖2中，哪個臺階更陡？

圖1

圖2

2.在圖3中，哪個臺階最陡？你是如何判斷的？

圖3

3.比較圖4中的兩個臺階，你有什么發現？

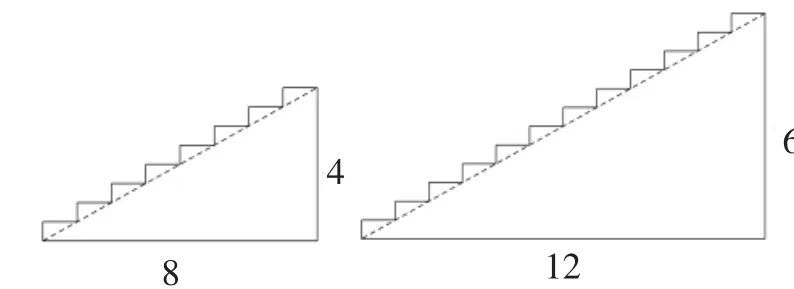
圖4

二、生活情境的解讀之道

現行蘇科版初中數學教材上的生活情境，絕大部分既有情境又有問題，但有的只有情境沒有初始問題，如正切的生活情境就不含初始問題.對于第二類，我們首先要根據生活情境創設一個指向本課研究核心的初始問題.如針對“某體育館為了方便觀眾，設計了不同坡度的臺階”的生活情境，我們可以先設計如下的初始問題.

初始問題：某體育館為了方便觀眾，設計了不同坡度的臺階.如果坡度太平，會影響后面觀眾的視線，而且需要體育館有更大的面積，如果坡度太陡，觀眾觀看時存在安全隱患.因此，臺階的坡度成了設計的關鍵.那么，坡度由什么決定呢？

1.從情境走向問題——借助生活現實解讀

義務教育數學課程標準指出，呈現內容的素材應貼近學生現實［4］，主要包括生活現實、數學現實、其他學科現實三方面.學生的后續學習總是基于已有的上述現實，生活情境中的實際生活經驗有助于學生理解初始問題，對初始問題做出最初的直觀判斷，從而把學生逐步引向數學思維的正確軌道上.如上述生活情境，我們可以給出如下借助生活現實的解讀，幫助學生從生活經驗出發，走向要探究的問題.

解讀1：圖5中的兩個臺階哪個更陡？

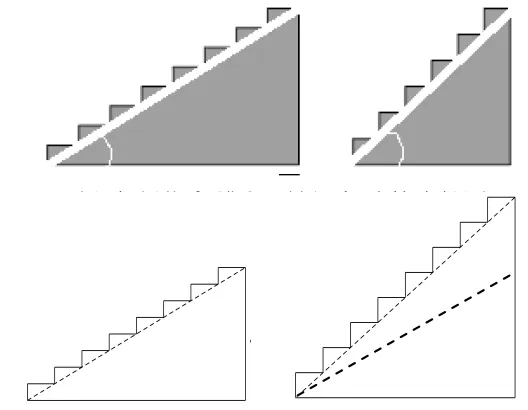
圖5

對于數學中的坡度，學生還不是十分清楚它的內涵，但生活中臺階的陡學生是有經驗的，如圖5，學生很快就可以得出第二個臺階陡的結論，進而得出“坡度可以由傾斜角來決定！臺階的傾斜角度越大，臺階越陡；臺階的傾斜角度越小，臺階越平”的結論.

2.從生活走向數學——完成數學抽象解讀

數學源于對現實世界的抽象，基于抽象結構，通過符號運算、形式推理、模型構建等，理解和表達現實世界中事物的本質、關系和規律.數學抽象包括從事物的具體背景中抽象出一般規律和結構，并用數學語言予以表征等［2］.生活情境不是數學，透過生活現象抓住數學本質的數學化過程才是情境的要義.如上述生活情境，我們可以給出如下完成數學抽象的解讀，幫助學生從生活現象走向真正數學.

解讀2：（1）圖中哪個臺階更陡？你是如何判斷的？

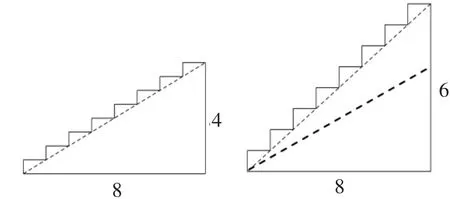
圖6

如果沿用上面傾斜角的視角可以直觀判斷出第二個臺階比第一個臺階陡；也可以把第一幅圖中的三角形平移到第二幅圖1中去，顯然由數學知識全量角大于部分角，得出第二個臺階陡；如果不借助生活經驗和數學平移，我們只能借助高度與寬度，可以得出“坡度也可以由垂直高度與水平距離一起確定！當水平距離相同時，垂直高度越高，臺階越陡；垂直高度越小，臺階越平”的結論.如果只有垂直高度或水平距離一個量，能確定坡度嗎？顯然不行.

（2）圖7中哪個臺階更陡？你是如何判斷的？

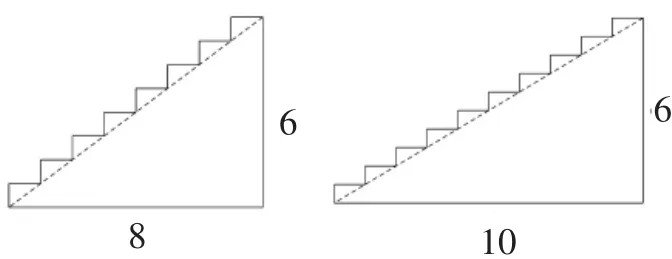
圖7

仿上可以得出“坡度也可以由垂直高度與水平距離一起確定！當垂直高度相同時，水平距離越短，臺階越陡；水平距離越長，臺階越平”的結論.

（3）圖8中哪個臺階最陡？你是如何判斷的？

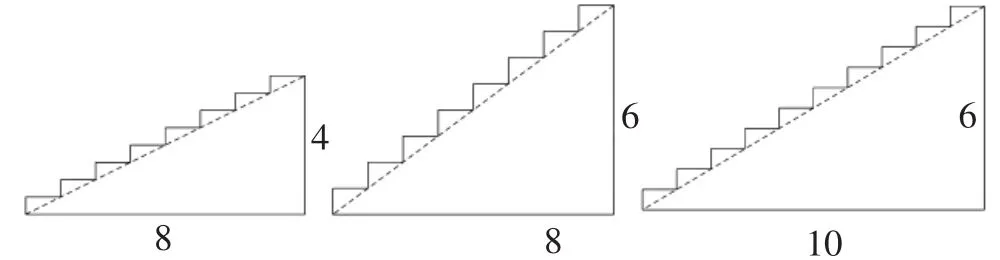
圖8

由上述（1）和（2）可知，第二個臺階最陡.得出“坡度也可以由垂直高度與水平距離一起確定”的結論，那么這兩者又是如何一起確定這個坡度的呢？通過和差積商進行嘗試，得出由垂直高度與水平距離之比確定.

（4）圖9中哪個臺階更陡？你是如何判斷的？

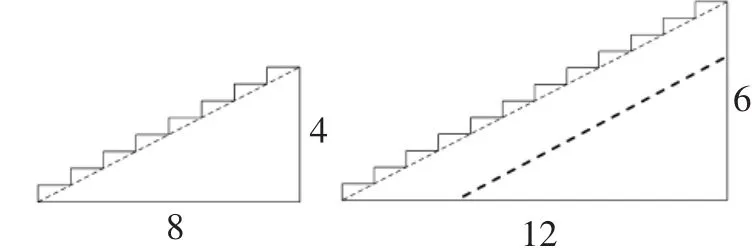
圖9

這兩個臺階的坡度直接借助傾斜角大小判斷有點難度；直接借助垂直高度與水平距離確定也有一點難度；把問題抽象成數學，就是要比較兩個直角三角形的相應銳角，如果把第一幅圖中的三角形平移進第二幅圖中，可以發現，這兩個三角形構成兩邊對應成比例并且夾角相等的相似形，因此得到對應角相等，進而這兩個臺階坡度一樣.

綜上所述，臺階的坡度可以直接借助傾斜角大小進行比較，傾斜角越大，臺階越陡；臺階的坡度也可以借助垂直高度與水平距離之比來確定，比值越大，臺階越陡.

3.從數學走向本質——利用邏輯推理解讀

邏輯推理是指從一些事實和命題出發，依據規則推出其他命題的素養.從生活問題走到數學問題之后，數學要向前繼續發展主要依靠數學的邏輯推理.如上述生活情境，我們借助生活現實、完成數學抽象后，就可以從數學內部視角進一步解讀，引向問題的深處與數學本質.

解讀3：上述五個問題，如果我們抽象成數學問題，相當于在研究一個直角三角形的問題.關于直角三角形，我們已經研究了什么呢？

（1）關于角：內角和、兩銳角互余；（2）關于邊：三邊不等關系、周長、面積、勾股定理、斜邊上的中線；（3）你還知道什么？你覺得對于一個直角三角形，還能研究什么？

在Rt△ABC中，∠A一旦確定，坡度就確定了.∠A越大，坡度越陡，∠A越小，坡度越小.同樣，在Rt△ABC中，a、b一旦確定，坡度也就確定了.說明∠A與a、b背后必定存在著聯系！而這正是剛才我們所猜測的還可以研究直角三角形邊與角之間的關系.下面就可以圍繞著∠A確定、也確定，∠A變化也隨之變化，展開銳角三角函數定義的教學.

生活情境源于學生的生活現實，指向數學的本質探究.所以，任何一個生活情境的解讀都必須體現借助生活現實、完成數學抽象、利用邏輯推理這三大過程，這也是基于數學學科核心素養的生活情境的解讀之道.從情境走向問題的生活現實告訴學生，數學來源于生活實際，提醒學生要時時處處關注來源于自然社會中的現象與問題，處處留心皆數學.從生活走向數學的抽象，可以引導學生用數學的眼光觀察世界.從數學走向本質的邏輯推理是數學知識形成的重要手段，更是培養學生用數學思維思考世界的必經之路.知識形成后的運用與應用等數學建模，有助于學生用數學語言表達世界素養的養成.由此可見，數學學科核心素養的落實應該貫穿于數學課堂教學的方方面面，貫徹于數學課堂教學的過程之中.