例談初中幾何證明中 “輔助線的自然生成

秦曉

[摘? 要] 輔助線是連接已知條件和所求結論的橋梁，是在分析條件、探索結論中結合所學概念、定理、幾何模型等相關知識自然聯(lián)想到的所需要的幫助. 因此，在具體的教學過程中，教師要力求向?qū)W生展示輔助線的生成過程，讓學生體會輔助線是怎樣在問題中“無中生有”的.

[關鍵詞] 橋梁;生成;感悟

1. 從幾何定理入手尋找輔助線的自然生成

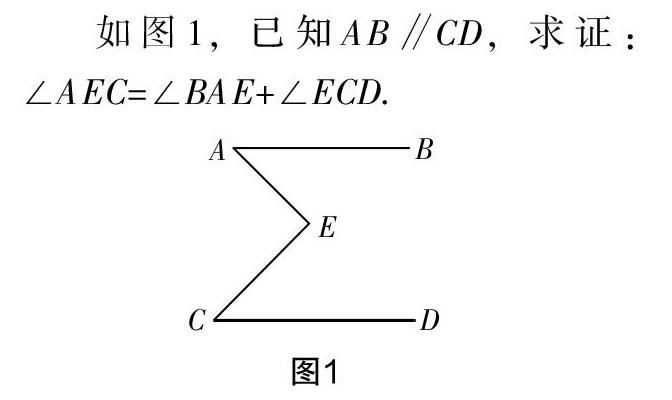
分析講解? 根據(jù)“平行線的性質(zhì)定理”：兩條平行直線被第三條直線所截，同位角相等，內(nèi)錯角相等，同旁內(nèi)角互補. 本題已知條件中出現(xiàn)了兩條平行直線，要求證的結論是角度之間的數(shù)量關系，這與平行線的性質(zhì)定理描述的內(nèi)容高度吻合，所以我們可以從這里找到破題點. 對比定理發(fā)現(xiàn)，這里缺少的就是第三條截線，所以我們可以從這個角度出發(fā)添加輔助線，構造截線，接下來就只需要思考可以怎么構造截線. 這個問題拋給學生以后，輔助線就在學生筆下自己長出來了，而且還不止一種方法，展示輔助線的添加方法如下：可以過點E作直線MN∥AB，如圖2;可以連接AC，如圖3;可以延長CE交直線AB于點F，如圖4;可以延長AE交直線CD于點F，如圖5.

啟示? 從定理入手，使得輔助線的出現(xiàn)有了“落腳點”，在熟悉、掌握定理的基礎上，可以很自然地得到輔助線，這是直接告訴學生：“平行線問題中遇到拐點就過拐點作平行線”是不能相比的.后者這樣直接灌輸，不僅容易遺忘，而且記住的學生也大都“消化不良”，在遇到類似問題時無法舉一反三.

2. 從幾何模型中尋找輔助線的自然軌跡

這個問題很多學生都覺得無從下手，本來準備就這個題給學生做一個仔細的評講，不過在評講的時候，一位學生主動請纓，說出了她添加輔助線的過程：從這個題目要解決的問題入手，求△ADE的面積，就聯(lián)系到三角形的面積公式——底乘以高除以2，那么就應該思考以△ADE的哪一邊作為底. 根據(jù)已知條件，三邊中已知AD邊為2，所以很自然聯(lián)想到過點E作EM垂直于直線AD，這樣就生成了解決這個問題的第一條輔助線. 可是問題還沒有徹底解決，這個時候我也思考了很久，發(fā)現(xiàn)DE=DC，而且還出現(xiàn)了兩個垂直關系，所以我聯(lián)想到平時學習過的“三垂直模型”，因此我嘗試著過點C作CN垂直于直線AD，如圖8所示. 通過△DME≌△CND，得到EM=DN，居然真的把這個題目做出來了，太讓我興奮了.一番描述行云流水，全班同學佩服得報以熱烈的掌聲.

啟示? 這道題目難度不小，但是學生的回答卻給了筆者很多啟發(fā)，因為每一條輔助線都來得那么自然，層層推進. 由三角形面積公式想到作高線，由高線帶來的垂直關系再結合CD=DE，聯(lián)系到全等中的“三垂直模型”，進一步轉(zhuǎn)化已知條件. 整個解題過程一氣呵成，酣暢淋漓，這不論對解題者還是參與傾聽的學生來說都會受益良多，也再次感受到了輔助線的自然生成有強大的生命. 這不僅使用了老師教授的輔助線的作法，而且也讓學生自己收獲了運用這種思維帶來的成果.

3. 從幾何圖形的對稱美中去發(fā)現(xiàn)輔助線的自然生成

很多幾何圖形，比如角、線段、等腰三角形、等邊三角形等都具有軸對稱性，它們的性質(zhì)，比如角平分線上的點到角兩邊的距離相等，線段垂直平分線上的點到線段兩個端點的距離相等，等腰三角形的“三線合一”也基本上來自于其圖形本身的對稱性，只不過當我們研究完這些性質(zhì)以后，更多的注意力放在了定理本身以至于忽略了它最本質(zhì)的特性. 比如這樣一個例題：如圖9，在△ABC中，已知AC>BC，CD平分∠ACB，求證：AD>BD.

啟示? 剛分析本題時，會讓人有摸不著頭腦的感覺，感覺一個明顯的結論就是無法通過推理得到，從而產(chǎn)生失落悵然. 如果能夠多體會角是一個軸對稱圖形，就算它的性質(zhì)定理也只是它的軸對稱性的一個特殊角度的展示;如果能從圖形本身的這種特征出發(fā)去解決問題，那么便會給我們很多題目的解決帶來啟發(fā)，也自然能尋找到輔助線的蛛絲馬跡.

4. 從結論的形式中去體會輔助線的生成

有一類幾何證明題，它的已知條件或者是結論里面有形如兩條線段的和（或者差）等于第三條線段，或者一條線段是另一條線段的兩倍，一個角是另一個角的兩倍等之類的描述，這種形式也蘊含著解題的思路，下面用一道例題加以展示：如圖11，CD為△ABC的中線，求證：CA+CB>2CD.

分析講解? 從已知條件入手似乎覺得沒有更多的解題思路了. 這個時候可以從結論入手，發(fā)現(xiàn)結論中出現(xiàn)了2CD，所以可以從這里出發(fā)找到本題的突破口，嘗試將CD延長加倍，延長CD至點E，使得CD=DE，然后連接AE，構造全等三角形.如圖12，△CDB≌△EDA，得到CB=AE，在△ACE中，利用三邊關系可得：AC+AE>CE，根據(jù)線段的等量代換得到CA+CB>2CD，得出證明.

啟示? 很多教輔書中都將這種方法稱為“中線倍長法”，筆者認為，除了介紹這種名稱外，更重要的是帶領學生一起去感悟“中線倍長”字面之外的含義，什么時候需要中線倍長？將中線倍長以后會得到什么樣的結論？這些結論結合其他常見的幾個圖形又會出現(xiàn)哪些常見的問題？這樣學生才會知道在哪些情況下需要把線段進行倍長，而不至于為了倍長而倍長，把某些簡單的題目反而復雜化.

輔助線的添加對于一道幾何題目而言是一個系統(tǒng)工程，每一種方法之間也不是孤立的，每一個學生看到一個已知條件聯(lián)想到的知識點也是不盡相同的，所以從每個人的思維之數(shù)上開出的花就是五彩繽紛的，這也形成了課堂的多樣變化深度以及廣度，讓每個學生在與別人的交流中碰撞思維（圖9的例題），在實際的授課中有的學生是從定理入手得到解決方案的，現(xiàn)在將他的思路展示如下：

看到已知條件中出現(xiàn)了角平分線，我首先想到的就是角平分線定理，所以我嘗試了做角兩邊的垂線段. 如圖13，過點D作DE⊥AC，DF⊥BC. 接下來我發(fā)現(xiàn)，除了得到DE=DF便無路可走了，再仔細一想，作了垂線段以后可以聯(lián)系到三角形的面積，嘗試這樣一思考，利用=，同==，進而得到=，因為AC>BC，所以AD>BD.

1. 關注學生的學情，用已經(jīng)掌握的知識推動思維的發(fā)展

學生才是學習的主體，教師所做的工作是為主體服務的. 這就需要我們深入了解我們的主體，知道他們現(xiàn)有的知識近區(qū)，加以引導，擴大他們的認知圈，為推動下一步的思維發(fā)展奠定基礎. 如果忽略了，不管教師自認為講解得多么透徹，學生聽來都是云里霧里，不知所云，更不用說知道學習了.

2. 教學過程注重“慢”的藝術

世間萬事的生成都是有過程的，需要時間的，所以在教學的過程中要有留白，有安靜的思考，有火熱的討論，有條理的交流，這些都需要執(zhí)教者有從容的心態(tài)，不怕學生花時間. 這樣的課堂可能例題的講解數(shù)量比較少，可是涵蓋的知識容量，以及衍生出來的學生對數(shù)學的興趣、感知的數(shù)學的活力、思維能力的提升等非智力因素卻會帶來事半功倍的效果.

3. 教學過程中注重學生模型思維的培養(yǎng)

在幾何證明中有很多從一般情況中提煉歸納出來的模型，可以強化這種模型意識，就是強化學生對概念、定理等知識的深入認識，讓學生少走彎路，提高成功的體驗率，有了一次次推理成功的通暢淋漓的感覺，學生學習數(shù)學的激情必定高漲，內(nèi)驅(qū)力帶來的效果是任何說教都替代不了.

4. 對于自然生成卻失敗的輔助線要有優(yōu)化的意識

學生在實際的操作中，根據(jù)自身的知識構建出一條輔助線，卻發(fā)現(xiàn)無法進行有效的推理，鉆進一個胡同然后毫無頭緒，可以另尋解決途徑，然而結合已知條件將輔助線進行優(yōu)化也不失為一條上策，用一個例題展示一下過程：如圖14，在△ABC中，∠CAB=∠CBA=45°，CA=CB，點E為BC的中點，CN⊥AE交AB于N. 求證：AE=CN+EN.

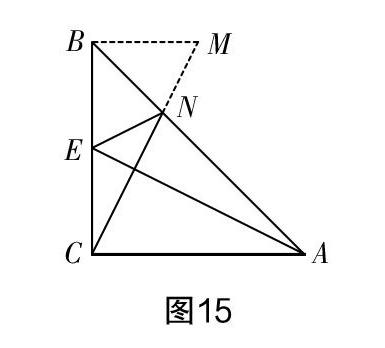
一個學生的分析過程：看到這個結論是線段和差的形式，所以想到嘗試用“補短”的方法來添加輔助線. 延長CN到點M，使得NM=EN，如圖15，可是在接下來證明△BEN≌△BMN，△BCM≌△CAE都遇到了問題，沒有辦法得出任何一對三角形全等，從而整個證明停滯不前，接下來準備放棄這種方法.

從“截長”的角度添加輔助線，這個思路非常清晰到位，不過第一種輔助線就一定要舍棄嗎？能不能通過再次分析題目的已知條件做個調(diào)整，△BCM與△CAE已經(jīng)有一對邊BC=AC，一對角∠BCM=∠CAE，所以在描述輔助線的時候可以換個角度，直接使得CM=AE，就可以補充這兩個三角形全等所需的第三個條件，進而證明△BEN≌△BMN，進一步推理根據(jù)線段的等量代換完成整道題目的證明.

啟示? 本題通過改變對輔助線的描述將一條被放棄的輔助線“起死回生”，這對那些有這種經(jīng)歷的學生有莫大的鼓舞. 在這種思維方式的啟發(fā)下，他們自己也很快找到了新的方法：過點B作AC的平行線交CA的延長性于點M或者過點B作BM⊥BC交CN的延長線于點M. 他們能這樣舉一反三，對筆者也是莫大的鼓舞.

幾何證明問題對輔助線的添加一直都是一個教師關注的熱點，也是一個老生常談的話題，怎么把這首老歌唱出新意，也是筆者在教學的過程中一直思考的問題. 通過對已知條件的挖掘，結合想得到的證明結果，尋找這兩者的連接點，如果之間的橋梁需要我們?nèi)ゴ罱ǎ涂梢詮膶嶋H需要出發(fā)，實現(xiàn)輔助線的有效生成. 以上的一些淺顯的個人想法希望能夠拋磚引玉，與同仁們一起探討輔助線自然生成的生長點，為我們的實際教學注入新的想法.