核心素養背景下初中統計與概率教學的思考

[摘? 要] 文章通過對近兩年福建省中考統計與概率類型題的詳細分析，深入解讀日常教學過程中如何更好地把握課本，并且結合數學核心素養的標準對教學提出了思考和建議.

[關鍵詞] 中考;統計與概率;概念;核心素養

新課程標準對統計與概率模塊的教學要求，是學生能夠理解隨機事件發生的可能性，體會樣本與總體的關系，體會頻率與概率的關系，并在實際學習過程中經歷數據收集、數據整理和分析的過程等. 只有在這樣的過程中，學生才能構建對于統計與概率的基本概念，并掌握它們的意義和求法，會繪制圖表，并進一步懂得它們常見的錯誤類型及改正方法.

下面我們結合最近幾年福建省中考統計與概率類型題的詳細分析，同時結合初中數學核心素養的觀念對相關問題進行解讀.

對題目的分析

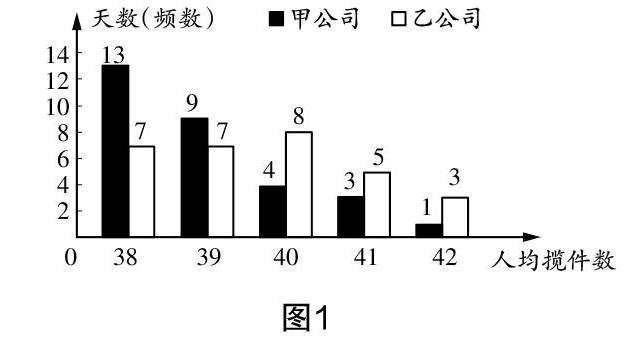
題目1? （2018福建卷第22題）甲、乙兩家快遞公司攬件員（攬收快件的員工）的日工資方案如下：甲公司為“基本工資+攬件提成”，其中基本工資為70元/日，每攬收一件提成2元;乙公司無基本工資，僅以攬件提成計算工資，若當日攬件數不超過40，每件提成4元，若當日攬件數超過40，超過部分每件多提成2元. 圖1是今年四月份甲公司攬件員人均攬件數和乙公司攬件員人均攬件數的條形統計圖.

（1）現從今年四月份的30天中隨機抽取1天，求這一天甲公司攬件員人均攬件數超過40（不含40）的概率;

（2）根據以上信息，以今年四月份的數據為依據，并將各公司攬件員的人均攬件數視為該公司各攬件員的攬件數，解決以下問題：①估計甲公司各攬件員的日平均攬件數;②小明擬到甲、乙兩家公司中的一家應聘攬件員，如果僅從工資收入的角度考慮，請利用所學的統計知識幫他選擇，并說明理由.

分析? 本題取材于當今社會的熱門話題：快遞公司攬件員的日工資方案. 甲、乙兩家公司方案不同，甲公司工資方案屬于簡單的一次函數關系，乙公司屬于分段函數，自變量取值范圍在40為分界點，所以在閱卷的過程中有一部分學生采用設函數解析式來回答本題，也是情理之中的. 本題如果從函數的角度去看，也是一道相當有價值的題目，以上是從題目條件方面去分析的.

如果我們從題目的問題入手分析就會發現，統計與概率的味道就凸顯出來了. 第（1）小題中，“30天中隨機抽取1天”以及“超過40（不含40）的概率”，問題非常清晰，背后隱含的考點：這是一個“隨機事件”，求該事件發生的概率. “甲公司攬件員人均攬件數超過40（不含40）”指令要求非常明確，觀察橫坐標，只有41，42符合，甲公司（即黑色部分）分別為3天、1天，滿足條件的有4天，而總數據條件也非常明顯，是“30天中”，從而該事件發生的概率，就可以根據定義得到答案.

第（2）小題①問，采用了“估計”這個專業術語，再加上“各公司攬件員的人均攬件數視為該公司各攬件員的攬件數”，不難發現背后隱含的考點是用樣本去估計總體的思想. “日平均攬件數”背后也隱含著一個專業術語“平均數”，在條形統計圖中，準確地說隱含著“加權平均數”的概念. 回歸課本我們發現，現行人教版八年級下冊112頁對加權平均數的定義嚴格來說是不夠完整的，是基于初中學生能夠理解的方式來進行表達的. 課本隨后給出了加權平均數的計算公式，結合公式給出定義：“叫作這n個數的加權平均數”. 從嚴格意義上來看，加權平均數是指不同比重的一組數據的平均數，具體來說，加權平均數就是“把一組數據按照合理的比例來進行計算”，也就是“將各個數值乘以相對應的權重值，然后相加進行求和得到總體值，最后除以總的單位數”. 其實現行人教版配套教師教學用書對加權平均數還有進一步解讀，“統計中常用平均數有算術平均數、調和平均數、幾何平均數等. 算術平均數分為簡單平均數和加權平均數兩種形式. 在統計學上，簡單算術平均數主要用于處理沒有分組的原始數據，而加權平均數只能用于已經整理歸類分組后的數據”. 我們進一步研究不難發現加權平均數的大小不僅受各組數據值大小的影響，而且受各組數據值出現的頻數大小的影響.

基于這樣的分析，如果在授課過程中我們以這樣的思維角度去備課，對知識點進行深入思考和研究，然后在教學中引導學生明白背后的這些道理，那么他們對于條形統計圖類型已經整理后的數據，求平均攬件數，就不難發現是求這一組數據的加權平均數，進而得到答案. 即①甲公司各攬件員的日平均件數為=39件. 真正的難點在于學生對核心概念的理解，錯誤往往是學生對概念背后所隱含的條件不清楚而產生的，在中考答題的時候出現千奇百怪的答案也就不足為奇了，這是我們在以后的教學中應該借鑒的.

第（2）小題②問，問題“僅從工資收入的角度”，背后隱含的信息就是告訴我們計算工資收入，但是題目“利用所學的統計知識”限制了我們解決問題的工具，明確告知所學統計知識，如：總體、個體、樣本、平均數、方差、標準差、眾數、中位數、頻數、頻率等. 而結合本題條件，甲公司攬件員的日平均工資為“基本工資+攬件提成”，即基本工資為70元/日+每攬收一件提成2元，需要用到第①問的日攬件平均數39，可以直接計算每天的平均收入，70+39×2=148元，也可以計算每月總收入：70×30+39×2×30=4440元. 而乙公司的收入計算方式，相對難度就大了一些. 因為有“日攬件數不超過40”和“日攬件數超過40”兩種情況，根據條件收入分別為：4元、6元. 而由①問的分析我們知道，條形統計圖最核心的問題是“權”，攬件數為38，39，40的權重分別為7，7，8，就可以計算攬件總數，每件收入是4元;而攬件數為41，42的權重分別為5，3，計算攬件總數，每件收入是6元. 這樣就可以計算最后的月總收入，當然如果計算日平均攬件數，也可以得到日平均收入. 這樣就可以對比得到的甲乙兩家公司的工資收入，從而幫助小明做出選擇.

通過以上的分析，我們發現審題能力是解決問題的一個關鍵，我們不僅僅要讀懂文字面上的含義，還要透過文字發掘背后所隱含的信息，這是一種非常重要的數學素養. 在研究中我們發現2016年后很多數學專家在研討初中數學核心素養的問題，我們一直認為初中學生通過數學學習培養他們閱讀、思考、表達三種能力是我們數學教學的目的. 閱讀是一個非常重要的素養，通過閱讀，能夠獲取我們所需要的信息，然后對所獲取的信息進行加工，內化為學生自己的東西，并通過思考，轉化為可以用語言（口頭和書面）進行表達[1]，這就是我們理解的數學素養. 在這個背景下，我們再看另一道關于概率統計的問題.

題目2? （2017福建卷第23題）某高校進行共享單車活動，每用單車一次，租金為0.5元. 現為了提高使用率，規定在一天內，對多次用單車予以優惠，每天第二次用單車起，每多用一次減0.1元，如表1.

（1）求a，b;

（2）共享單車租賃公司為了了解是否盈利，從該校5000名學生中抽樣調查了100名學生每天用單車情況，情況如表2. 若該共享單車租賃公司每天要付成本5800元，問該公司是否盈利，并說明理由.

分析? 本題背景過了一年多來看依然十分新穎，共享單車已經成為城市發展過程中十分重要的一個角色，審題能力、閱讀理解能力依然是考查的基本. 第（1）小題的題面信息：“每用單車一次，租金為0.5元”“每多用一次減0.1元”，問題是求a，b的值，再結合表格中所列舉的“0.5，0.9”，其實隱含的信息就是在解讀題面“每次0.5元，每多用一次減0.1元”，所以不難得到，每天用3次付租金為：a=0.5+0.4+0.3=1.2元，每天用4次付租金為：b=0.5+0.4+0.3+0.2=1.4元. 每天用5次付租金題目條件已經給出了，目的是為了幫助學生檢驗前面3次和第4次用車所付的租金是否正確.

第（2）小題，題設直接就出現“抽樣調查”，隱含了對總體、樣本、樣本的容量、頻數等概念的考查，經過整理后的數據以表格的形式出現，其實類似于條形統計圖，權重對最后的數據分析有很大的影響. “5000名學生中抽樣調查100名學生”，背后隱含的信息是需要用樣本去估計總體的思想，所以需要計算樣本的平均租金，很明顯需要使用加權平均數的公式進行計算得到1.1元，然后用這個平均數去估計總體的情況，進而求出租金收入5000×1.1=5500元，最后跟“共享單車租賃公司每天要付成本5800元”較比得出所需要的結論.

經過研究對比，我們可以發現近兩年福建省統考的統計題綜合程度高，考查的知識點與能力要求較強. 這兩題所考查的知識點都含有概率、加權平均數、條形統計圖，同時考查了學生的運算能力、推理能力，以及學生對數據分析、應用意識及統計與概率的思想的掌握情況. 《新課程標準》（2011版）在課程設計思路中有對統計與概率進行詳細的描述，“數據分析觀念包括：①了解生活中一些問題，我們應當先做調查研究來進行數據收集，然后通過科學的分析就能夠弄清楚數據中蘊涵的信息，最后對要研究的問題做出判斷;②了解對于同樣的數據，我們可以有不同的分析方法，要求我們能夠根據問題的背景以及我們的需求選擇合適的方法;③通過數據分析去真正體驗隨機性. ” [2]

基于此，在核心素養的觀念下我們可以進一步解讀統計與概率的內容對于培養初中學生的數學核心素養應包括以下三個互相關聯的要素：一是要有大數據意識. 要了解生活中的問題，可以并需要用數據來描述和刻畫，為此應當先做抽樣調查或者普查，然后收集數據，最后通過分析做出判斷. 二是能夠選擇適當的方法搜集和分析數據. 要了解對于同樣的數據可以有不同的分析方法，我們需要懂得根據問題的背景選擇合適的方法，不同的統計方法沒有簡單意義上的“對”與“錯”，只有“好”與“不好”. 三是能夠通過數據分析的過程去體驗隨機性. 數據的隨機性主要有兩層含義：一是對于同樣的事情，每次收集到的數據有可能是不同的;二是只要有足夠的數據，我們就可能從中發現規律.

從第2小題第（2）問的解答過程也發現，按初中《新課程標準》中所述對基本統計量的要求，有一部分學生已經達標，同時也有了一定的統計意識，但在運用的過程中，對基本統計量的理解是否到位還存在問題. 而這個問題背后最根本的原因還是對于概念的理解，特別是統計相關概念在學生心里形成的系統觀念. 通過學習概率與統計的知識，學生將其內化為屬于自己的東西，構建自己的知識體系，這才是初中統計與概率教學真正意義上的目的，從而形成學生對于社會現象的分析、對世界的認識，這才是數學核心素養最核心的體現.

對教學的啟示

結合上面對兩道中考試題的深入分析，我們發現一份中考試卷除了選拔功能之外，更大的意義是對來年中考方向的指引和對一線教學的指導. 通過對一份試卷，甚至是一道題目的分析和反思，我們可以發現日常教學過程中存在的問題，借助這樣的分析，可以進一步加深自己對教學的認知，形成自己的教學風格或者教學主張. 特別是對初三教學和復習都有特別大的指導意義，比如通過對以上兩道概率與統計問題的分析，我們可以發現日常教學中的方向.

1. 審題能力培養是關鍵

比如題目要求“請利用所學的統計知識幫他選擇，并說明理由”，在閱卷過程中有部分學生使用一次函數求出解析式，根據解析式來回答問題，他們忽略了“所學的統計知識”這樣關鍵性的界定. 目前初中階段所學統計知識基本包括：平均數、加權平均數、中位數、眾數、極差、方差、各類統計圖、樣本估計總體等.

2. 概念教學是重點

對于題目要求學生選擇合適的統計量進行說明，很明顯考查學生對概念的理解，以及靈活應用的能力. 平均數、加權平均數之間的區別和聯系，都需要在日常教學中讓學生真正理解其來龍去脈，弄清概念的內涵和外延，而不僅僅是會背公式、背解題套路. 比如2018年福建中考第22題第（1）小問求概率的問題，在閱卷過程中發現一部分學生還是利用畫樹狀圖的方式來解決，為何會出現這種現象？背后傳遞出什么樣的信息？我們在日常教學過程中如何才能避免學生出現類似的問題呢？其實這些問題都是非常有價值的，可以帶給我們一線教師很多的思考. 然后沿著這個思路深入去做研究，去做數據對比，就會發現我們的教學還有很多可為之處.

3. 計算能力培養不容忽視

學生計算能力不足的問題在統計與概率題目中再一次凸顯出來，由于題目所給數據比較多，計算量比較大，很多學生計算能力不足的問題就顯露無遺了. 反思教學，從初一“有理數”單元開始，教師應該如何教才能夠從源頭解決學生計算能力不足的問題？比如在教學中很多“負負得正”這樣的結論，我們應該如何正確解讀？是讓學生去背誦這樣的口訣，還是從算理、算法入手，從概念入手，讓學生經由自己的閱讀，主動獲取文本的信息，然后經過內在的加工，轉化為自己的語言進行描述和表達. 我們還發現學生運算能力背后是對核心概念、算理、算法的理解和掌握.

4. 進一步挖掘考題的潛在價值

對于2018年福建中考第22題值得一線教師進一步挖掘其潛在的價值，由于本題所給出的數據較特殊，因此本題從平均數、眾數，或是中位數三種角度得到的結果都是選擇乙公司. 但在教學過程中我們可以引導學生從這三種不同的角度去解釋問題時，仍需要從數據的實際意義去解釋. 比如詢問學生，用這三個數據進行對比，你認為有什么不同？為什么用平均數來說明比其他兩數更合適？為什么本題不能用方差來解釋？通過這樣的深入分析和反思，使學生對概念的理解進一步加深，從而提升思維層次，取得更好的教學效果.

我們一直相信數學核心素養必須在實際教學中才能真正得到落實，比如統計與概率是互聯網時代大數據背景下數學應用的一個重要體現，數據分析已經深入到現代社會的各個領域. 所以在日常教學活動中，培養學生數據分析素養的形成過程中，要注重學生養成通過分析數據發現規律，進而解決問題的習慣[3]. 特別是學生對于基本概念的理解，對于通過閱讀題目挖掘文本背后所隱含信息的能力的培養都是十分重要的，只有這樣我們才能真正做到通過數學培養學生核心素養的目的.

參考文獻：

[1]丁耀星，段振富. “先學后導，合作探究”教學模式研究課題總結[J]. 中學教學參考， 2016（27）：6-8.

[2]中華人民共和國教育部. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[3]段振富，劉曉艷.? 例談建立軸對稱模型解決數學問題[J]. 數學教學通訊，2014（1）：62-64.

基金項目：本文系福建省“十三五”第一批中學數學學科教學帶頭人培養對象科研課題《基于核心素養的初中數學單元教學設計研究》階段性成果，立項編號：DTRSX2017012.

作者簡介：段振富（1976-），教育碩士，中學一級教師，福州市骨干教師，從事中學數學課堂教學模式、中學生數學學法指導、小初銜接專題研究等.