“自我實(shí)現(xiàn)式”的源與流教學(xué)提升學(xué)生的數(shù)學(xué)核心素養(yǎng)

於青

摘 ?要：讓高中生以“自我實(shí)現(xiàn)式”獲得數(shù)學(xué)新知是數(shù)學(xué)教學(xué)追求的境界，更期望以此提高學(xué)生的數(shù)學(xué)核心素養(yǎng)。鑒于數(shù)學(xué)學(xué)科特點(diǎn)，教師在教學(xué)過程中需要更注重在源頭上加以引導(dǎo)，讓學(xué)生形成自己的流程從而獲得數(shù)學(xué)新知，也就是所謂的源與流的教學(xué)。本文以引入課、性質(zhì)課、習(xí)題課教學(xué)為入口，著重分析由此學(xué)生獲得數(shù)學(xué)新知的有效性。

關(guān)鍵詞：自我實(shí)現(xiàn);源與流;新知;有效性;數(shù)學(xué)核心素養(yǎng)

新課程改革“以學(xué)生發(fā)展為本”，使學(xué)生在數(shù)學(xué)知識(shí)、思維方法以及理性精神等方面得到發(fā)展，為學(xué)生終身發(fā)展奠定良好的基礎(chǔ)。我國教育部在下發(fā)的相關(guān)意見中指出：學(xué)生的核心素養(yǎng)，主要是指學(xué)生應(yīng)具備的適應(yīng)終身發(fā)展和社會(huì)發(fā)展需要的必備品格和關(guān)鍵能力。理解核心素養(yǎng)，應(yīng)該強(qiáng)調(diào)的不是知識(shí)和能力，更應(yīng)該是獲得知識(shí)的能力。

這一理念要求教育理性回歸，即回歸生活實(shí)際，體驗(yàn)數(shù)學(xué)知識(shí)的“源與流”。要求學(xué)生既會(huì)“打的式的問路”，又會(huì)“自我實(shí)現(xiàn)式的問路”。因此，回歸數(shù)學(xué)新知以達(dá)到自我實(shí)現(xiàn)成為高中數(shù)學(xué)教學(xué)亟待解決的問題，因?yàn)橐磺袛?shù)學(xué)能力的培養(yǎng)和形成有賴于新知的學(xué)習(xí)過程。重視以“自我實(shí)現(xiàn)式”獲得數(shù)學(xué)新知是當(dāng)下數(shù)學(xué)教學(xué)的一條有效途徑。

一、引入課教學(xué)的源與流

問題一：國際象棋起源于古代印度，相傳國王要獎(jiǎng)賞國際象棋的發(fā)明者，需要獎(jiǎng)賞什么？發(fā)明者說：“請(qǐng)?jiān)谄灞P的第1個(gè)格子放上1顆麥粒，第2格放上2顆，第3格放上4顆，依此類推，每個(gè)格子的麥粒數(shù)都是前一個(gè)格子里放的麥粒數(shù)的2倍，直到第64個(gè)格子便可。”國王欣然答應(yīng)。假定每粒麥子的質(zhì)量為0.4kg，據(jù)查，目前世界年度小麥產(chǎn)量約6億t，根據(jù)以上數(shù)據(jù)，判斷國王是否能實(shí)現(xiàn)他的諾言？

源：等比數(shù)列求和

流：第一，學(xué)生探索：S64=1+2+4+8+…+263……①式

即S64=1+2+22+23+…+263

第二，教師提問：如何求得S64的結(jié)果？（學(xué)生陷入沉思）

師：回顧等差數(shù)列求和公式是怎樣推導(dǎo)的？（從學(xué)生最近發(fā)展區(qū)點(diǎn)撥）

生：“倒序相加”

師追問：“倒序相加”的目的是什么？（再搭腳手架）

生：通過和式中“不變量”的合并，減少和式的項(xiàng)數(shù)。

師：那么該如何解決這一問題？等差數(shù)列求和是怎么做的？

在教師引導(dǎo)下，學(xué)生緊緊圍著“減少和式項(xiàng)數(shù)”這關(guān)鍵性目標(biāo)進(jìn)行思考，有的已發(fā)現(xiàn)。

生：①式兩邊同乘以2以后得②式，①與②兩式中絕大部分的項(xiàng)是一樣的，類比等差數(shù)列求和公式推導(dǎo)時(shí)用的“①+②”，這里“①一②”就可以正負(fù)抵消了，過程如下：

2S64=2+22+23+···+263+264……②即：S64=264-1

師：①式兩邊為什么要乘以2？ 乘以其他數(shù)是否可行？

反思：上述學(xué)習(xí)環(huán)節(jié)，教師從數(shù)列求和的流，引導(dǎo)學(xué)生回歸到等比數(shù)列求和的源，學(xué)生從等差數(shù)列的“倒序相加”自我實(shí)現(xiàn)了等比數(shù)列的“錯(cuò)位相減”，從知識(shí)的產(chǎn)生與發(fā)展過程中領(lǐng)會(huì)知識(shí)的本質(zhì)屬性。“為什么在②式的兩邊同乘公比”這一事實(shí)，為學(xué)生推導(dǎo)等比數(shù)列求和的一般式及今后進(jìn)一步運(yùn)用“錯(cuò)位相減”法求和打下堅(jiān)實(shí)的基礎(chǔ)。

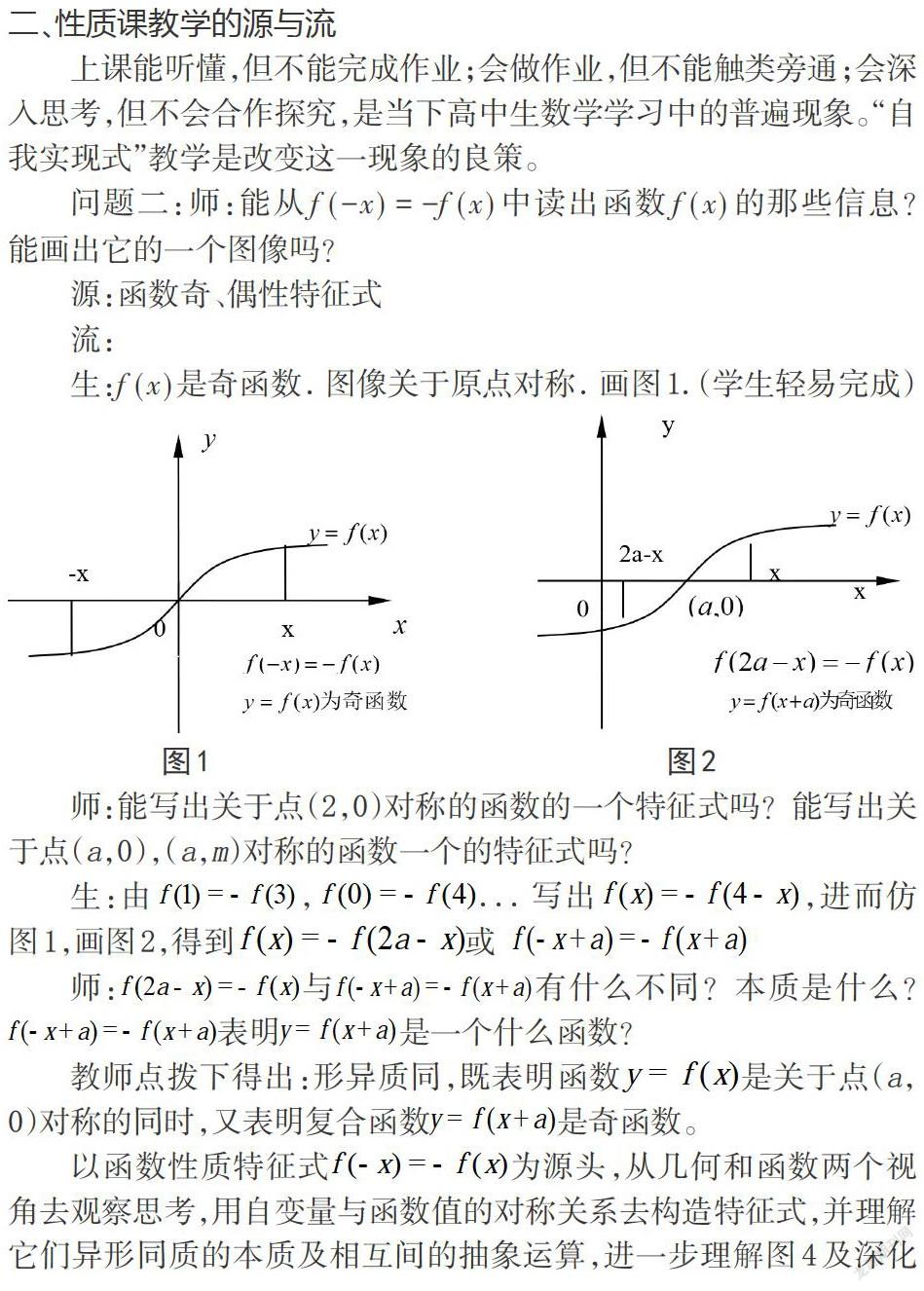
二、性質(zhì)課教學(xué)的源與流

上課能聽懂，但不能完成作業(yè);會(huì)做作業(yè)，但不能觸類旁通;會(huì)深入思考，但不會(huì)合作探究，是當(dāng)下高中生數(shù)學(xué)學(xué)習(xí)中的普遍現(xiàn)象。“自我實(shí)現(xiàn)式”教學(xué)是改變這一現(xiàn)象的良策。

反思：以“自我實(shí)現(xiàn)式”獲得數(shù)學(xué)新知是解決課堂效率低下的有效途徑。教師感嘆課堂教學(xué)效率低下，同一類型的題目一而再，再而三的講練，結(jié)果是領(lǐng)會(huì)者甚少。學(xué)生對(duì)課本新知識(shí)、例題解法、證明是被動(dòng)接受。一些完美的解法、技巧，絕好的證明途徑雖使學(xué)生聽后感到奇妙，但遇到實(shí)際問題時(shí)學(xué)生仍是一籌莫展，一團(tuán)霧水，以致教師感嘆：“課上講得清清楚楚，明明白白，課后做得糊里糊涂，不明不白。”其根本原因是學(xué)生對(duì)課本新知識(shí)、例題解法、證明是被動(dòng)接受，沒有達(dá)到自我實(shí)現(xiàn)，更無從談起素養(yǎng)的培養(yǎng)提高。正如數(shù)學(xué)家波利亞的言論：“學(xué)習(xí)任何知識(shí)最佳途徑是自我實(shí)現(xiàn)，因?yàn)檫@種自我實(shí)現(xiàn)理解是最深的，也最容易掌握其中的內(nèi)在規(guī)律、性質(zhì)和聯(lián)系。”故，源與流的教學(xué)，能幫助學(xué)生以“自我實(shí)現(xiàn)式”獲得數(shù)學(xué)新知，適應(yīng)高中數(shù)學(xué)學(xué)習(xí)，達(dá)到“自我實(shí)現(xiàn)“的結(jié)果，從而提升學(xué)生的數(shù)學(xué)核心素養(yǎng)。

參考文獻(xiàn)

[1]中華人民共和國教育部.普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017版）[M].北京：人民教育出版社，2017.

[2]高中數(shù)學(xué)《必修1》《必修4》《必修5》《選修2-1》[M].人民教育出版社A版.

[3]馬云鵬.關(guān)于數(shù)學(xué)核心素養(yǎng)的幾個(gè)問題[J].課程教材教法，2015（09）.