高三數學一輪復習如何做才更有效
——以“任意角的三角函數復習課”為例

黃兆海

傳統的高三一輪復習課遵循常態的復習課模式：考綱解讀——考題欣賞——考點梳理——典例分析——變式訓練——課時小結六個環節進行復習，課后再布置作業讓學生反復訓練；這樣的復習方式給學生的感受就是做了很多的題目，但是說不出學到了什么，遇到一些變式題還是不會做。本文以“任意角三角函數復習課為例”，談談為提高高三一輪復習的有效性的具體做法。

一、研讀考綱，復習要源于課本，但高于課本

高考命題不會過分追求知識的覆蓋率，因此在教學時應該緊扣考試大綱，抓好三基，既要全面復習又要重點突出主干知識；又因為《考試大綱》與去年相比應該不會有太多的變化，在復習時，若只是把高一、高二的內容又串講一遍，或是依托教輔資料的編排順序復習，如此效果往往并不好。其實在復習的過程中，應該要用好課本，充分發揮教材中例題的典型作用，在沒有扎實抓好基礎知識之前就去攻難題、搞綜合提高，肯定不會有好的效果。其實，我們都清楚高考數學試卷中有相當多的試題是課本上基本題目的直接引用或稍作變形而得來的，因此，復習要源于課本高于課本。

問題一.請同學們梳理一下：我們學過哪些三角知識？

設置該問題引導學生對學習過的三角函數的知識進行初步梳理，以形成對所學的三角知識有一個整體把握。

生A：“三角函數的定義，圖像與性質，三角恒等變換的公式”。生B補充：“角的定義，弧度制，同角三角函數關系，誘導公式還有正、余弦定理”。

二、注重知識的結構化，建立知識聯系網絡

問題二.對三角函數這一章進行系統梳理，分別說說各部分學習了哪些內容并指出它們之間的聯系。

隨后讓學生閱讀課本解決問題，展示生D和生E的梳理結果此目的是為了讓學生在知曉“問題一”的前提下明確各部分的細節——研究內容及方法，做進一步的具體化并理清各細節之間的聯系，不僅要教授復習內容，還要傳授復習方法，這么做比只是按照課本的復習順序更易于讓學生對本章書的知識結構有所了解，兩個問題過后實際上給了學生一個好的結構，一個好的框架，正如人教版編者陶偉林教授的觀點就是“給學生一條線把散落的珍珠（暗指知識點）一顆一顆的串起來，而不是一盤散沙；要給學生一碗面條，而不是一碗漿糊。”

課堂教學中常遇到這么一種現象，學生在解題時往往是苦思冥想而找不到思路，但經老師一提醒便茅塞頓開，這說明他們其實已經掌握了解決問題所需的一些概念和定理等知識，只是不知道如何運用。基于此，為學生構建一個良好的知識網絡方能有助于提高其解決數學問題的能力，而一輪復習要做的事正莫過于此。在具體操作上我們可以從讓學生自己看課本的目錄開始，讓他自己去歸納和整理，把每一個章節的知識用樹形圖的形式整理出來并下功夫去進行記憶，課堂上完成不了的，也可以把對具體內容的系統梳理作為作業布置下去。

三、直擊真題，有的放矢

問題三、看看近三年與三角部分知識有關的高考題，它們主要考查了哪幾類具體問題？（以下節選部分投影內容）

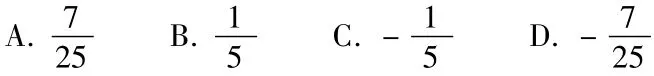
（2016課標II·13）△ABC的內角A、B、C的對邊分別為a、b、c，若cos，cos，a＝1，則b＝______.

生F：“主要有用三角公式來求值，解三角形等問題；”

師：“回答的很好，從近三年的課標卷高考題來看主要考查以下問題：（1）三角函數的圖像與性質；（2）解三角形。”

直接讓學生接觸高考真題能讓學生更早知道高考考什么？怎么考？有的放矢可以讓他們更易于發現自己應在那些知識與問題上著手進行復習，當然這一過程我只是要求學生分析高考題的考查內容，而不用具體求解出結果，畢竟在復習的初步這些問題對他們而言還是比較難，還需要教師對其進行二次加工，將其中綜合性較強的問題分解成一些具體的小問題，這就可以利用我們手頭的教輔資料來進行了，不依賴于一本教輔資料而是集各家之所長為我所用。

四、關注知識由來，避免機械記憶

很多學生在做題時只注重于記憶和運用公式的結論，對公式的來源不夠重視，導致一些題目稍作變式他們便束手無策了，究其原因就是因為平時僅是機械地記憶公式，對于知識與公式的內涵、意義并不作過多了解。

在高三的一輪復習當中要讓學生關注知識點的由來，而不僅僅是完成教輔資料上知識點的填空練習或者是機械的去背記公式，為此，我把考點梳理部分的內容分解成八個問題，把例題與練習融入到這些問題之中，讓學生通過分小組探究的形式自己推導公式，然后推選出中心發言人來解釋概念、公式的由來或是給出推導過程，讓學生自己教會自己，這么做比起學生填空，老師講解效果要好得多。明代學者陳獻章有云：“前輩學貴有疑，小疑則小進，大疑則大進。”在每個小組展示完畢后，我就讓學生進入設疑與答疑環節，體現一題多變，一題多解，與多解歸一的解題思維訓練。

總之，高三一輪復習只要教師重視為學生搭建知識的框架結構及各知識問題間的聯系，認真研究近三年的高考試題，并會“自主拆分真題”，用好課本，不迷信教輔，讓學生在知識與高考題的海洋中自由的徜徉，讓他們一開始就揭開了高考題的“真面目”，這樣的一輪復習一定會更有效。