重思維訓練促思維發展優思維品質

薛群

[摘 要]每一門學科都強調學生要學會觀察，數學作為一門自然科學，更應把學生觀察能力的培養和訓練作為教學的重要內容和目標。只有不斷打破學生已有的認知平衡狀態，把學生從思維的慣性中拽出來，讓他們重新審視自己的思維，才能激起學生求知的欲望，培養學生善于打破常規的思維力。

[關鍵詞]數學;思維;觀察;訓練;轉化;化歸

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2019）26-0077-02

數學是圍繞數量關系和空間形式來鍛煉和培養學生思維能力的一門理性科學，如何提升學生的形象思維能力和抽象思維能力是數學教師經常思考的課題。要達到數學學科的培養目標，必須從學生的心理發展和思維年齡特點出發，遵循認知規律，激發學生的情感需求，牢牢把握數學學科和數學教學是思維訓練這個本質特征。重思維訓練、促思維發展、優思維品質，方能達成數學教學的目標。

一、觀察求全

每一門學科都強調學生要學會觀察，數學作為一門自然科學，更應把學生觀察能力的培養和訓練作為教學的重要內容和目標。科學來源于觀察，觀察是眼、手、腦等多種感覺器官的綜合使用。在教學中，不少學生不會觀察，缺少觀察的方法，更不擅長把觀察和思考聯系起來，“觀”缺法、“言”無序、“思”欠深是學生數學學習困難的重要原因。現以蘇教版教材六年級下冊第77頁的習題為例，談談怎樣培養學生的觀察力。

6.先觀察前兩題的計算過程，再照樣子計算后三題。

我先引導學生仿照前面兩題的算法，算出第三、四兩題的得數，然后提問：“第五題還需要一步一步去計算嗎？你有什么快速寫出第五題得數的方法？”學生立刻報出第五題的得數為888880，但此時學生只是依葫蘆畫瓢，對這組算式的結構和各部分之間的關系并沒有科學而清晰的認識。為了把學生的思維缺陷暴露出來，把學生的積極性調動起來，我拋出問題：“你能正確填寫嗎？”

這個問題逼迫學生再次好好觀察這組算式的結構和各部分之間的關系，重新審視自己的思維過程，養成全面觀察、精細觀察、深刻思考的習慣。

首先，我引導學生整體觀察：算式中的符號只有“×”和“-”;得數越來越大;得數的位數從兩位數開始依次多一位。其次，我引導學生做精細觀察：第一個乘數位數依次多一位，數字排列是從9倒寫;第二個乘數不變，都是9;減號后面的減數從1開始依次增加1;得數個位都是0，其他數位都是8。最后，我引導學生發現各部分之間的大小關系，這是全面掌握這組算式結構和關系的重要一步，必須引導到位、有序觀察、深刻思考、全面表達。如第一個乘數的位數正好和減數的大小一樣，得數中8的個數和減數的大小一樣，得數的位數比第一個乘數的位數多一，第一個乘數個位上的數字和減數的和為10，等等。

只有按照從整體到部分再回到整體的觀察順序和方法，學生的觀察才是真正的觀察，而不僅僅是看或瀏覽。現在不少學生往往喜歡走馬觀花、蜻蜓點水式的觀察和學習，不能靜下心來有序有法地觀察，這個問題需要引起數學教師的高度重視，在低年級就注重培養學生的觀察能力和學習定力，否則學生的數學悟性就無從談起。

二、訓練求變

一線教師都有這樣的感覺，不少學生學得很死板，教一題會一題、不教不會，時間長了還會忘，讓他們舉一反三簡直比登天還難。導致這種現象的原因很多，其中一個重要的原因與教師有關——教學缺少變式、缺少變化、缺少溝通和聯系，還缺少整體觀念。如果我們的教學就題講題，學生又怎么能觸類旁通、舉一反三呢？教學就應求變、求異。我經常和學生講：“世界上唯一不變的就是變。”只有不斷打破學生已有的認知平衡狀態，把學生從思維的慣性中拽出來，讓他們重新審視自己的思維，才能激起學生求知的欲望和善于打破常規的思維力，這樣的教學才能靈活多變、常教常新。如，在教學“圓錐的體積”時，我就出了一組題目：

1.一個圓錐形鉛錘，底面半徑為6厘米，高為8厘米，求這個鉛錘的體積。

2.一個圓錐形鉛錘，浸沒在一個底面半徑為8厘米的圓柱形容器中，這時水面上升了1.5厘米，求這個鉛錘的體積。

3.一個圓錐形鉛錘，底面半徑為6厘米，浸沒在一個底面半徑為8厘米的圓柱形容器中，這時水面上升了1.5厘米，求這個鉛錘的高。

4.一個圓錐形鉛錘，底面半徑為6厘米，高為8厘米，把它浸沒在一個底面半徑為8厘米的圓柱形容器中，這時水面高度為10厘米，那么浸沒前容器中的水面高度是多少厘米？

題1是求圓錐形鉛錘的體積，有部分學生會忘記公式中的“[13]”，但更多學生在平時的機械練習中形成了思維定式——求圓錐形物體的體積一定要乘[13]。這種不看問題情境、不審數量關系的不良習慣一旦形成，會造成學生僵化的思考陋習。對題2的解答能有效打破這種思維定式。該題中，圓錐形鉛錘的體積和1.5厘米高的圓柱形水柱的體積相等，求圓錐形鉛錘的體積是替換成1.5厘米高圓柱形水柱的體積來算的，當然是用圓柱的體積算法計算。這樣一來，求圓錐形物體的體積一定要乘[13]的錯誤觀念不攻自破。題3是圓錐體積公式的逆向使用，已知圓錐體積和底面積求高，逆向用公式就是體積乘3除以底面積，從順向思考到逆向思考，同中有異、異中求活、打破套路。題4是圓柱、圓錐體積算法的綜合應用，我把教學的著力點放在一題多解上，啟發學生用多種解法解題，如10 - [13π×6×6×88×8×π]，或（82π×10 - [13π×62×8]）÷82π，還可以用方程或比的方法解，等等，這里就不一一贅述了。

要想學生活學、學活，教師首先要活教、教活。活水是新鮮的、變化的，“問渠哪得清如許，為有源頭活水來”學生活學的源頭就在教師平時的教中。

三、思路求通

轉化（化歸）是數學中常見的一種解題策略和數學思想方法，也是順利實現思維同化，構建數學知識體系最常用的一種教學方法。所謂生題熟做，正是化歸的重要價值和一般的思考方向。在平時教學中，我向學生提出方法大于解法，因此思路必須求通，“通”既是融會貫通，也是“化”，有轉化的意思，也有優化的取向，同時還有簡化的要求。王陽明的《傳習錄》中言：“讀書須入化境。”實際上學數學也是要臻至化境方能舉重若輕，抓住本質一擊而中。

學生在五年級知道了圓周長是直徑的π倍，圓面積是半徑平方的π倍，到了六年級學習圓柱時，又發現圓柱側面積是軸截面面積（沿底面直徑垂直切割得到的長方形截面）的π倍。三個“π倍”讓學生被數學的奇妙深深吸引。數學題之間的聯系和溝通能激發學生自主建構知識體系、體悟數學思想方法。下面以教學圓和圓柱的一組習題為例，談談思路求通的做法。

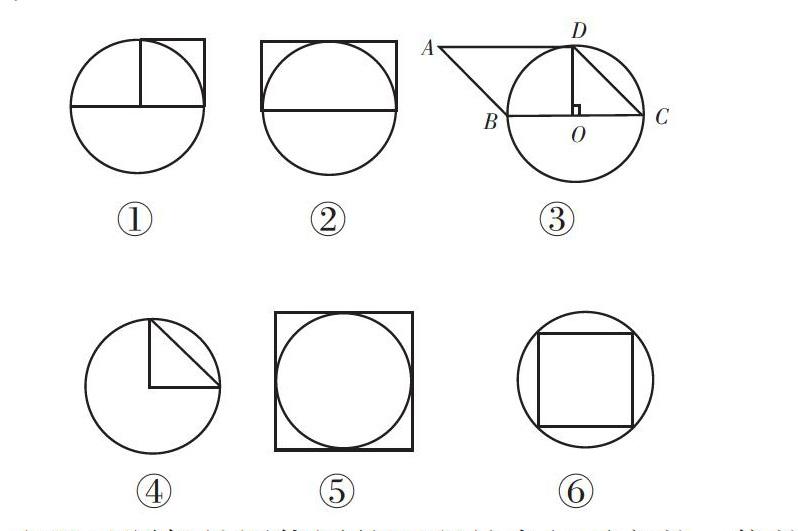
習題：1.如圖①，正方形的面積是9平方厘米，圓的面積是多少？如果正方形的面積是8平方厘米，圓的面積是多少？

2.如圖①，圓的面積是25.12平方厘米，你能求出正方形的面積嗎？

3.如圖②，長方形的面積是8平方厘米，圓的面積是多少？

4.如圖③，平行四邊形的面積是8平方厘米，圓的面積是多少？

5.如圖④，三角形的面積是8平方厘米，圓的面積是多少？

6.如圖⑤，正方形的面積是8平方厘米，圓的面積是多少？

7.如圖⑥，正方形的面積是8平方厘米，圓的面積是多少？

這組習題都是圍繞圓的面積是半徑平方的π倍的數量關系展開的，萬變不離其宗。這樣的題組設計不是簡單的重復，而是同中見異、異中有同，有效激活了學生的思維，更有助于推動學生思維的螺旋式上升。學習素材之間的內在聯系不斷推動學習者去尋找數學的奧妙，使之在變與不變之中把握數學本質。又如：

8.用一個正方體木塊削成一個最大的圓柱，這個圓柱與正方體的體積比是多少？

9.用一個正方體木塊削成一個最大的圓錐，這個圓錐與正方體的體積比是多少？

8、9兩題的加入，又引領學生的思考走向了更靈活、更多元、更深刻的遠方，數學知識的系統性和綜合性在這組層層深入的習題中得到了淋漓盡致的展現，且學生的探索活動一直在進行，知識體系的建構在化歸中悄然成型，方法的優化也在問題導向中悄然完成。

數學是訓練學生思維最好的一門學科，只有發揮學科特色，抓住數學本質，重思維訓練、促思維發展、優思維品質，才能使全面提高學生數學素養的目標有抓手、有突破、有成效。

（責編 李琪琦）