瞻前顧后，為整數乘法畫句號
——《三位數乘兩位數》教學設計

張 慧

【教學內容】

人教版四年級上冊第47 頁。

【教學過程】

一、前概念再現

師：同學們，我們學過三位數乘一位數和兩位數乘兩位數，你們會筆算145×2 和45×12 嗎？

學生獨立計算，集體訂正，回憶兩位數乘兩位數的計算方法。

【設計意圖：調動學生已有知識經驗，為自主建構新知識做鋪墊的同時，為培養遷移能力和感受乘法知識連貫性埋下伏筆。】

二、自主遷移，建構新知

師：三位數乘一位數和兩位數乘兩位數你們已經會算了，我們今天一起來研究《三位數乘兩位數》。

1.審題并列式。

出示例題：李叔叔從某城市乘火車去北京用了12 小時，火車每小時行145 千米。該城市到北京有多少千米？

學生審題并列式：145×12。

2.借助估算，判斷乘積所在區間。

師：有四位同學已經嘗試筆算145×12，你能不能一眼看出他們當中誰算錯了？

課件出示：①145×12=740

②145×12=1600

③145×12=1740

④145×12=3040

生：①錯了，最小的三位數和12 相乘都超過了1000。

生：④錯了，把145 看成150，12 看成20，得數才是3000。

【設計意圖：估算一直是學生學習的一個難點，因此，本設計靈活處理教材，將直接估算145×12的取值范圍改為判斷別人的計算結果是否正確的方式呈現，雖然降低了難度，但學生仍然獲得了估算的機會。】

3.自主探究計算。

師：②、③哪個錯了？請同學們筆算一下，看看到底等于多少。

學生獨立計算，一人板演。

全班匯報計算過程。

【設計意圖：用估算的辦法不容易判斷②和③究竟誰對誰錯，想解決這個問題還得借助于筆算，而筆算的方法與學生原有的兩位數乘兩位數算法是相同的，因此可以放手讓學生利用前概念獨立計算出得數。】

4.概括并驗證算法。

師：同學們會計算這個三位數乘兩位數的題目了，那如果有人問你三位數乘兩位數怎樣算，你怎樣講給他聽呢？

四人小組概括算法。

生：末位對齊；從個位乘起；兩位數的個位與三位數乘，積的末位與個位對齊；十位上的數與三位數乘，積的末位與十位對齊。

師：計算兩位數乘兩位數時，個位上的數與第一個因數乘，積的末位與個位對齊；三位數乘兩位數時，個位上的數與三位數乘，積的末位就一定與個位對齊嗎？

生：個位上2×145 等于290，是290 個“一”。

師：十位上的乘積呢？

生：1450，也就是有145 個十。

師：我們總結出了三位數乘兩位數的計算方法，一起來讀一讀。

【設計意圖：三位數乘兩位數可以讓學生自主遷移兩位數乘兩位數的算法來總結新算法，而后經歷質疑與驗證，將兩位數乘兩位數的算理再加工，從而理解三位數乘兩位數的算理，并驗證對于三位數乘兩位數與兩位數乘兩位數算法相同的猜想。】

5.多位數乘三位數。

師：如果百位上的數與三位數乘，積的末位應該與哪一位對齊，表示什么？

生：表示有幾個百，與百位對齊。

師：千位上的數乘呢？

生：與千位對齊，表示有幾個千。

【設計意圖：三位數乘兩位數是整數乘法的結束課，學生在本節課中不僅要建構三位數乘兩位數的計算方法，同時又要向多位數乘多位數的計算遷移。在本環節中，學生借助計數單位來解釋乘法的意義，在思考某一位上的數與三位數乘的意義中感受到了知識是可延伸的。】

6.兩位數十位上的數與三位數百位上的數相乘。

師：同學們已經掌握了三位數乘兩位數的方法，剛才老師請同學們判斷了四位同學的做法，其中第一位同學錯在哪里呢？

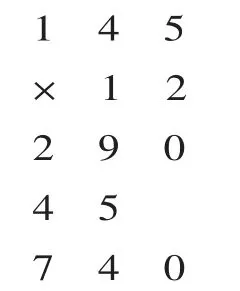
生：漏掉了十位上的“1”與百位上的“1”相乘所得的“1”。

7.小結——延伸。

師：1740，這個計算結果對嗎？我們用計算器檢查一下吧。

師：三位數乘兩位數與兩位數乘兩位數一樣，不管個位上的2 與45 相乘還是與145 相乘，積的末位我們都是與個位對齊，表示多少個一；十位上的數去乘，積的末位都與十位對齊，表示多少個十。原來三位數乘兩位數的算法和兩位數乘兩位數的算法是一樣的。如果再有兩位數乘四位數，怎樣算呢？

生：算法與三位數乘兩位數一樣。

【設計意圖：教學不能止步于知識的傳授，還要將數學知識進行適當的拓展和延伸。】

三、鞏固提升

1.豎式計算，建立模型。

師：看來同學們學會了三位數乘兩位數的算法，請你在練習紙上試著計算下面兩題吧。

獨立計算后，投影個別學生的練習并集體說理。

師：假如不給你具體的數字，你能說說各部分表示什么嗎？

師：第一個框表示什么呢？

生：表示多少個“一”。

師：下面的方框表示什么呢？

生：表示有多少個“十”，與十位對齊。

【設計意圖：通過直觀圖的形式幫助學生建立筆算乘法的模型。學生借助模型，從宏觀上再次理解筆算乘法的意義，使得乘法的意義在學生心中一般化。】

2.54×145。

師：再來試試這一題吧，想一想用什么方法好呢？

學生獨立計算后，展示兩種不同計算方法。

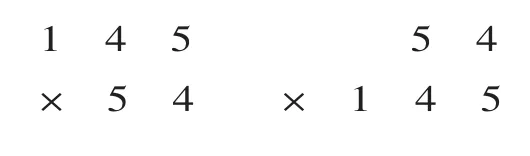
師：這兩位同學的計算方法不同，計算結果都正確。你覺得兩種計算方法哪種好？

生：第一種好，把145 放上面只有兩行算式，54 放上面有三行算式，容易錯。

師：雖然把54 放上面容易出錯，老師還是想問問第三行的54表示什么呢？

生：54 個“百”。

師：經驗告訴我們把數位多的數寫在上面不容易出錯。

【設計意圖：本題兩種解法都對，但學生要會選擇最優的方法，因此提倡學生交換兩個因數的位置，用145×54。學生通過互相啟發，發現“兩乘加”要比“三乘加”計算起來更容易。】

3.滲透數學文化。

師：同學們，這是古代歐洲計算三位數乘兩位數的方法，你能看懂嗎？

學生解釋計算過程。

師：這幾個“6”是什么意思呢？

生1：第一個6 是個位的3與十位的2 相乘得到的，表示6個“十”。

生2：第二個6 表示6“百”。生3：第三個6 表示6 個“十”。師：有人說，筆算三位數乘兩位數就是算算有幾個“一”、幾個“十”、幾個“百”，最后把幾個“一”、幾個“十”、幾個“百”加起來，有道理嗎？

【設計意圖：滲透了數學文化的同時又逐步分析了筆算乘法意義，拓展學生的視野。學生在這道題目中感受到了計算方法多樣性和文化的多樣性。】

四、總結延伸

師：同學們猜，如果以后再學習乘法，會學習什么內容呢？

生1：四位數乘三位數。生2：五位數乘四位數。

師：猜錯了，以后都不學多位數的筆算乘法了，知道為什么嗎？

生：和三位數乘兩位數的計算方法一樣。

師：我們學了三位數乘兩位數，以后遇到多位數乘多位數的時候可以用三位數乘兩位數的方法來計算。