尺規作圖教學用力點在哪兒
——由尺規作圖的作業批閱說起

江蘇省蘇州市胥江實驗中學校 蔣 凱

一、由尺規作圖的作業批閱說起

八年級上學期初學全等三角形、軸對稱、線段垂直平分線之后，學生都會使用尺規作圖進行一些基本作圖，如角的平分線、線段的垂直平分線等.但是階段檢測時，往往都會考查以下一個經典的尺規作圖問題（見圖1），根據教學經驗，總有一些學生不能得到這個題目的滿分.很大比例的學生只是畫對角平分線，但線段垂直平分線的作圖不正確（見圖1）.

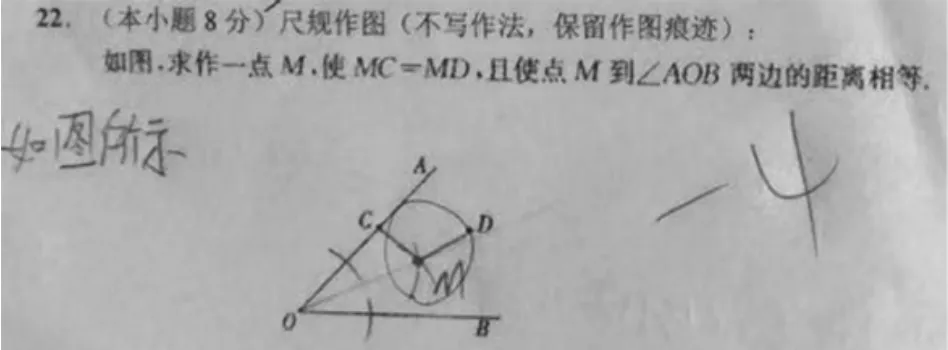
圖1

線段的垂直平分線是基本作圖之一，教師上課時都會組織學生學習并教授作圖方法.然而，從批閱反饋情況來看，恐怕關于尺規作圖的作圖教學是“低效”的.

二、尺規作圖的教學用力點在哪兒

1.教師要先安排學生分析作圖條件

作圖之前需要先安排學生認真分析題意，想清問題的條件與作圖的目標與方向，然后畫出示意圖進一步分析作圖的可能性，以及作圖之后圖形具有哪些特征，需要運用哪些幾何性質.在此基礎上，再構思作圖的步驟與先后次序，然后初步規劃作圖方案，并利用限定的作圖工具開展作圖.如果教師缺少上述讓學生充分審題的教學環節，則學生往往就是被動模仿操作步驟，對問題的本質不甚清楚，難以達到深刻理解的程度，也缺少了審題教學這個前置環節.

2.教師要重視示范并教授作圖步驟

在審題之后，學生基本想清了草圖示意，規劃了作圖流程，這時教師要重視親自示范并教授作圖步驟，而不能以播放PPT來代替操作示范.當前，教育信息化、現代化裝備不斷更新升級，有些教室黑板的功能幾乎都被電子屏取代，有些教師甚至一節課都不進行板書，只是在PPT或電子屏上進行一些演算、標注，然后一屏接一屏往下翻，學生難以形成整節課板書的整體結構之感，重要的板書內容、作圖痕跡、作法依據，應該一直保留在黑板的顯著位置，讓學生能長時間關注，形成較強的視覺印象，促進他們深刻理解.

3.作圖之后需要引導學生進行證明

作圖之后，不能急于開展同類練習，以大量練習來訓練學生作法的熟練程度，而應該通過“拉長”對經典問題的理解時間來實現深刻理解這類問題.比如，尺規作圖之后，要引導學生進行證明，證明時需要調動已有知識、經驗進行推理論證，可以想清辨明作法背后的依據，體會幾何作圖的操作可能與步步有據.而且在證明之后，還可以促進學生對相關幾何定理的關聯理解，使學生知道數學知識的前后一致與邏輯嚴謹.也可以這樣說，單獨一道尺規作圖題僅是一道習題，但如果要求學生把作圖問題作為一個項目來研究，包括審題、作圖、證明、下結論，這樣就經歷了一個完整的項目化研究.

想起一道經典的選擇題，如圖2，是作角平分線的尺規作圖及痕跡，畫圖依據主要體現了全等三角形的哪一個判斷依據？

根據教學經驗，很多學生都會錯選為“SAS”.

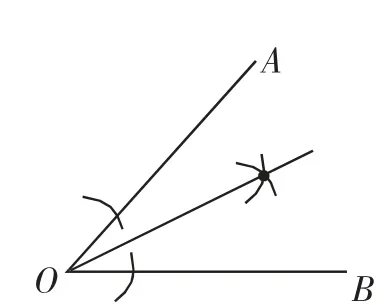
圖2

三、對“掐頭去尾，只燒中段”尺規作圖教學的進一步反思

尺規作圖是經典平面幾何問題，歷史悠久、博大精深.初中階段只是涉及一些基本作圖及初步運用，并不提倡探究一些較難的尺規作圖問題.下面略做一些梳理，并針對“掐頭去尾，只燒中段”式的作圖教學提出一些反思和建議.

案例1：作線段的“和、差、倍”

這種作圖題常常給一條線段或兩條線段，然后求作一條新的線段，新線段與已知線段是和、差或倍數關系.教學時如果直接示范教授作法，讓學生模仿作圖步驟，而不說清道理，就是典型的“燒中段”教法.完整的教學，可以先引導學生分析待作的線段與已知線段有什么關系，再安排學生畫出草圖分析，然后擬定可行的畫圖步驟，想清順序，再下手作圖，作圖之后要結合圖形標注恰當字母，進行簡單的示意與推理說明.

案例2：已知底邊及底邊上高的長求作等腰三角形

給定底邊及底邊上的高的長（也就是兩條線段的長），要求作出符合要求的等腰三角形，這是一個經典尺規作圖問題.如果直接給出（復制）一條線段（假設為底邊），然后作出它的垂直平分線，進一步，在垂直平分線上截取出高的長，最后寫出三角形為所求，這是典型的“燒中段”教法.完整的教學，先引導學生分析問題的條件（即題設），然后畫草圖分析：需要滿足什么條件？如何實現？作圖的順序怎樣確定？哪些步驟涉及了基本的尺規作圖？這些都應該在動手作圖之前有清楚的思考，然后就“了然于胸”，有條不紊，漸次作圖.作圖之后，寫出結語，繼續給出證明，由作圖出發利用線段垂直平分線的性質，證明所作三角形有兩邊相等，從而確認所作三角形是符合要求的等腰三角形.如果班級學生整體水平較高，還可進行變式拓展，引導學生思考和挑戰：

變式拓展題：已知兩條線段的長（長度不等），求作等腰三角形，使腰長為較長線段，一腰上的高為較短線段的長.

教學組織：安排學生先經歷畫草圖分析，構思作法，實施作法，這里初步涉及了所謂“奠基三角形”的思路，并且可以與全等三角形判定方法（“斜邊、直角”即HL法）進行關聯理解.當然，這道拓展作圖題，最大的問題在于漏解，因為滿足條件的三角形并不唯一，對于培養學生思維的嚴謹性也有很好的訓練價值.在此基礎上，還可跟進一道學生以前做過的易錯題.

同類練習：已知等腰三角形一腰上的高與腰的夾角為50°，求該等腰三角形頂角的度數.

案例3：作三角形的外接圓與內切圓

九年級學習圓的內容之后，三角形的外接圓、內切圓的概念就陸續出來了.這時尺規作圖作出一個三角形的外接圓、內切圓就是學生應該掌握的.實際教學進程中，不少學生往往停留在簡單模仿層面，能畫出一個三角形的外接圓，但并不知道或不深究其中的“簡化”作圖的道理.比如，作出一個三角形的外接圓，只需要作出三角形任意兩條邊的垂直平分線，以它們的交點為圓心，該圓心到三角形任意一個頂點的距離作為半徑畫圓即可，三角形的外接圓作好之后，還需要進行證明，為什么此時三角形三個頂點恰在同一個圓上？也就是尺規作圖的第三個教學環節，作圖之后的證明環節必不可少.而這種證明又可以與八年級學生初學全等三角形后，所學習的角平分線的性質與判定定理進行有效關聯，體會數學內容的前后一致、邏輯嚴謹.類似的，三角形內切圓的作圖教學也有這樣的特點，只要作出兩條內角平分線的交點（即三角形內心），再過內心向邊作垂線段，該垂線段的長即為內切圓的半徑，從而可實現成功作圓.接著安排學生進行證明，關聯理解八年級時所學過的命題“求證三角形三條內角平分線交于一點”.

四、寫在后面

教學即研究，一線教師在繁重的日常教學工作中如何擺脫“西西弗斯推巨石上山”的繁雜無趣呢？也許把日常教學工作中的“手頭小事”都當成教學研究的素材來思考、研究，就是一種防范職業倦怠的有效方法.事實上，面對一些經典問題，學生掌握的效果不好，更多的情況應該是反思我們的教學方式與教學方法，而不是埋怨學情，因為很有可能是教師非常熟悉經典問題的處理流程，卻忽略了學生的最近發展區，想當然地認為學生也應該很熟悉這些經典問題.想來，這也就是章建躍先生倡導的“理解學生”的重要涵義吧.