“析”運算能力障礙 “尋”培養能力途徑

葉燕華

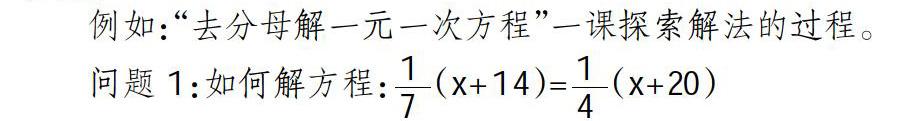
【摘 要】運算能力是課標關注的核心能力，是學生數學學習的“童子功”，也是學生數學學習的重要基礎。但初中生普遍存在“運算能力障礙”。為了提高學生的數學運算能力，教師應深入分析學生的運算錯誤原因，針對學生實際，引導學生重視基礎、明算理、講算法，細觀察、勤思考，培養學生的思維能力，提高學生的運算能力。

【關鍵詞】數學運算能力;障礙;途徑

運算能力是初中數學的基本能力，運算能力對學生數學學習質量起關鍵作用。因此，在中小學數學的教學中，教師都十分重視對學生運算能力的培養。盡管如此，運算問題仍是初中生在學習中遇到的最大障礙之一，經常出現運算速度慢、計算準確率低，在考試中數學成績甚至于物理、化學成績都不理想的現象。而不少教師和學生對運算能力的理解不到位，常常將運算過程中的錯誤原因歸結為學生的“粗心大意”“機械照搬公式”“盲目演算”等，究其深層原因，是學生的思維模式、學習方法及教師的教學方法未能達到靈活運用運算能力的要求。因此，深入分析學生在數學學習中的運算能力障礙，針對學生在運算過程中所暴露的問題，找出解決方法，才能盡可能地提高學生的數學思維能力。

1.初中生數學運算能力障礙分析

1.1學生不重視對基本概念的理解與掌握

從學生的答題情況和得分數據分析來看，學生對數學基本概念、公式的運用掌握得并不盡如人意。學生在運算過程中，往往是某個環節出現了問題，如數學概念不清、運算公式記錯、解題基本方法掌握不充分等，導致整個運算的錯誤。

1.2學生不重視算理算法的學習過程

例如，2016年漳州質檢卷第8題：若-2a<-2b，則a>b，其根據是（? ? ）

A.不等式的基本性質1? ?B.不等式的基本性質2

C.不等式的基本性質3? ?D.等式的基本性質2

本題考查不等式的基本形式，不僅要學生會解不等式，還要了解每一步的理由依據。在考后的試卷分析中，出人意料的是：此“送分題”變成了“送命題”，很多學生答錯。學生在學習過程中，教師比較重視對其運算技能的訓練，采用題海戰術，進行大量的機械性練習，但不重視培養學生發現、推導、證明運算法則的能力，學生缺乏對算理的理解，僅是機械性地選擇算法，雖然在一定程度上形成了技能，但并沒有真正提高學生內化算法算理的能力。

2.培養學生運算能力的途徑

2.1夯實基礎知識，確保運算的準確性

《課標》指出：“運算能力是指能夠根據法則和運算律正確進行運算的能力。”能否準確理解和靈活掌握各種運算所需的數學概念、運算公式、法則，以及學生是否對數學概念、運算公式、法則的理解深刻，都直接影響到算法的選擇與運算準確度。如果數學概念模糊，運算公式、法則混亂，必定會影響學生的運算能力。為了提高學生的運算速度，確保準確率，教師在平時的教學中，可以讓學生先從概念、性質、公式和法則的理解入手，著重掌握好有關運算的基礎知識和基本技能，提高解題的準確性。

2.2重視算理、算法，保證運算的合理性

運算的合理性是運算能力的核心。它要求運算過程要符合算理，每一步都應有理有據。這就要求學生明算理，合理地尋找最佳運算途徑。如一個法則的推導，得出過程通常包含對概念的理解、方法的概括歸納及數學表達，這是一個思維訓練的過程，是運算合理性的表現。在推導中有時還會出現一題有多種不同的運算途徑，繁簡不同，則需加以比較，選擇最佳解法、最優算法。因此，在平時教學中，教師要讓學生在弄懂、弄通必要的算理、算法、算律上多下功夫，同時注重培養學生一題多解的能力，講究算法，鼓勵學生對一道題進行多角度、多方位的探索，逐步達到合理算法、提高運算能力的目的。

例如：“去分母解一元一次方程”一課探索解法的過程。

學生活動：限時讓學生獨立解答，多數學生會利用學習過的去括號法解方程。

問題2：同學們在完成哪一步時花的時間較多？是否有更簡便的方法呢？

（教師提示：與上節課所學不同的是這個方程的系數是分數，不好計算，還容易出錯，大家是否有辦法把分母去掉，將分數化為整數？）

教學分析：在教師的提示下，讓學生大膽嘗試，想辦法在已有知識的基礎上，化未知為已知，化繁為簡，讓學生體會轉化的數學思想，學會選擇最優算法。

師生活動：學生展示交流，討論如何解含分母的一元一次方程。

問題3：解法依據是什么？

教學分析：以此問題強調解方程的每一個步驟都需要有理有據，教師在教學過程中，培養了學生明算理、講算法的數學運算能力。

本節內容其實沒有新知識，關鍵是培養學生的運算能力，使其通過對算理算法的思考，深刻理解解方程的新方法。教學中講究算法，揚長避短，減少出錯的機會，盡量以最短的時間得到正確的結果，這樣又能培養學生的算理能力，在不斷比較、選擇中，學生在多解的思路中選擇的合理解法，明確算理。

2.3深入思考，培養運算的靈活性

在很多情況下，數學運算是在一定情境中進行的，結合具體情境抽象出運算對象是解決問題的首要任務，結合情境探索運算思路是解決問題的關鍵。因此，教師需要在研究常規算法的基礎上，深入研究非常規算法，使學生學會選擇適當的運算方法，靈活設計運算程序，成功解答。這一過程不僅是要培養學生的運算能力，還需培養學生數學思考和問題解決的思維能力。

例如，在“運用平方差公式因式分解”的教學中，教師設計了這樣一道具有挑戰性和新穎性的題目：設a=192×918，b=8882-302，c=10532-7472，則a，b，c的大小關系是? ?。在解題過程中，大部分學生純粹計算，結果耗時費力且正確率還不高。但若能深入思考就能發現，第二和第三兩項可以利用平方差公式進行因式分解：

b=（888-30）（888+30）=858×918，

c=（1053-747）（1053+747）=306×1800=306×3×600

=600×918，a=361×918所以a

再如，已知x2-x-1，求x4-3x2的值。如讓學生先解方程再直接代入求值，會比較繁瑣。對此，教師可引導學生構建新的算法，結合解一元二次方程的降次轉化思想，得到x2=x+1，x4=x2+2x+1=x+1+2x+1=3x+2，于是x4-3x2=3x+2

-3（x+1）=3x+2-3x-3=-1。

根據以上例子可以看出，題目的非常規解法通常是來源于對原題結構的思考，同時進行相應的解構和重建構，則解題具有較強的靈活性與技巧性。所以，在平時教學活動中，教師要經常和學生一起探索問題的非常規解法，深入觀察分析運算對象，提高學生的運算能力。

運算能力培的養是一個長期的過程，教師在教學中要認真傾聽學生的思考過程，及時發現學生運算錯誤的原因，有針對性地加強學生對運算意義的理解，不僅教會學生計算，還要使學生明算理、講算法，注重數學思考與問題解決，讓學生學會選擇適當的運算方法，優化運算過程，只有這樣，才能有效發展學生的運算能力。

【參考文獻】

[1]徐建.關注運算能力，培養核心素養[J].中學數學參考（中旬），2018（8）：64-66

[2]楊九詮，李鐵安.義務教育課程標準（2011年版）案例式解讀（初中數學）[M].教育科學出版社，2012：30-34

（本論文系2018年度漳州市基礎教育教學研究課題 《學科交叉條件下的初中生運算能力培養探究》，立項批準號：ZPKTY18024。）

（福建省漳州市第五中學，福建 漳州 363000）