高三復習專題
——概率統(tǒng)計解答題

梁麗怡

(佛山市第三中學 廣東佛山 528000)

關于概率統(tǒng)計的專題復習，高水平的學校更多的是放手讓學生刷題，因為本身內(nèi)容難度不大，但是隨著閱讀量的增大，動輒幾百字的文章讓人云里霧里，加之繁雜的計算，這些都是失分的原因。針對以上兩大問題，筆者在今年備考中，對概率統(tǒng)計這一部分中常失分的兩類題型作了以下分析：

一、決策問題

在此類型問題中，閱讀量較大，涉及社會的各項措施，和實際生活聯(lián)系緊密，具有重要的應用意義。決策問題實際是在不同的情況下進行分析計算，實際上就是分段函數(shù)，通過分段計算從而達到利益最大或者損耗最小的目的，實際應用性很強。這也是學生最陌生、最無從下手的類型。

例（2016 全國1 文18）：

某公司計劃購買1臺機器，該種機器使用三年后即被淘汰。機器有一易損零件，在購進機器時，可以額外購買這種零件作為備件，每個200元。在機器使用期間，如果備件不足再購買，則每個500元。現(xiàn)需決策在購買機器時應同時購買幾個易損零件，為此搜集并整理了100臺這種機器在三年使用期內(nèi)更換的易損零件數(shù)，得下面柱狀圖：

記x表示1臺機器在三年使用期內(nèi)需更換的易損零件數(shù)，y表示1臺機器在購買易損零件上所需的費用（單位：元，n表示購機的同時購買的易損零件數(shù)）

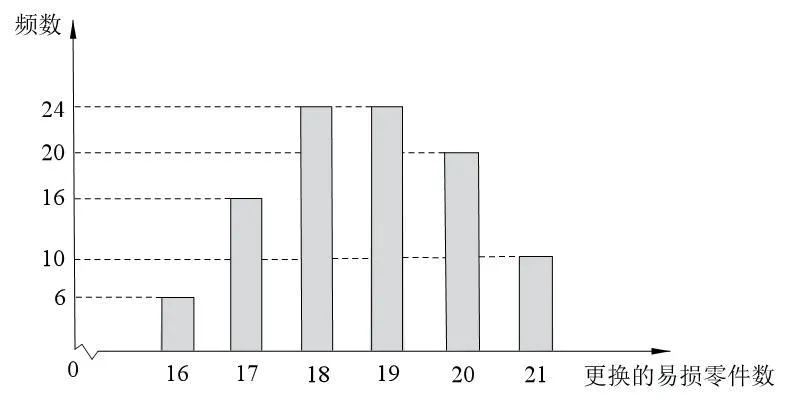
（I）若n=19，求y與x的函數(shù)解析式；

（II）若要求“需更換的易損零件數(shù)不大于n”的頻率不小于0.5，求n的最小值；

（III）假設這100臺機器在購機的同時每臺都購買19個易損零件，或每臺都購買20個易損零件，分別計算這100臺機器在購買易損零件上所需費用的平均數(shù)，以此作為決策依據(jù)，購買1臺機器的同時應購買19個還是20個易損零件？

解：（Ⅰ）當x ≤1 9 時，y=3 8 0 0；當x ＞1 9 時，y=3800+500(x-19)=500x-5700，所以y與x的函數(shù)解析式為

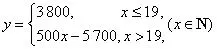
（Ⅱ）由柱狀圖知，需更換的零件數(shù)不大于18的頻率為0.46，不大于19的頻率為0.7，故n的最小值為19。

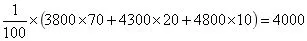
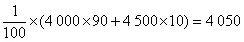
學生在閱讀時受到x，y，n多個自變量的影響，搞不清楚x，y之間是分段函數(shù)的關系。此時先讓學生在“現(xiàn)需決策在購買機器時應同時購買幾個易損零件”這句話中體會到是決策問題，分段的原因是買多了備件可能會造成浪費，但買少了卻需要更高的單價購買零件。那么應當是根據(jù)三年使用期內(nèi)需更換的易損零件數(shù)的調(diào)查結果計算所需費用的平均數(shù)，比較大小后便可做出決策。第（1）問中n=19，則x≤19是費用就只是原件和備件的總和；如果x＞19，則需要增加另外購買的易損零件數(shù)的費用，而購買數(shù)目是x-19。其實這也是商家的常用促銷手段，比如說商品的售后期隨著費用增長而延長。教學時多舉例，才能讓學生體會到概率統(tǒng)計是和實際生活密不可分的。

二、線性回歸問題（非線性回歸問題）

回歸問題往往要計算回歸直線的斜率和截距，為了簡化計算，條件會有參考數(shù)據(jù)，但可能有些是與題目無關的，這就需要學生在運算中注意等價代換，尤其是非線性回歸問題有換元這步，更要注意這點。

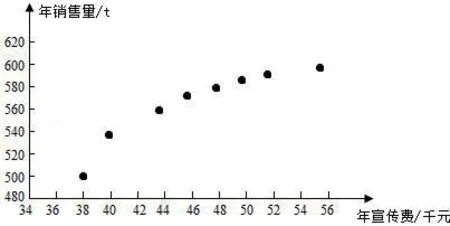
例：某公司為確定下一年度投入某種產(chǎn)品的宣傳費，需了解年宣傳費xi（單位：千元）對年銷售量yi（單位：t）和年利潤z（單位：千元）的影響，對近8年的年宣傳費xi和年銷售量yi（i=1，2，…，8）數(shù)據(jù)作了初步處理，得到下面的散點圖及一些統(tǒng)計量的值。

?

（Ⅱ）根據(jù)（Ⅰ）的判斷結果及表中數(shù)據(jù)，建立y關于x的回歸方程；附：對于一組數(shù)據(jù)（u1v1），（u2v2）…（unvn），其回歸線v=α+βu的斜率和截距的最小二乘估計分別為：

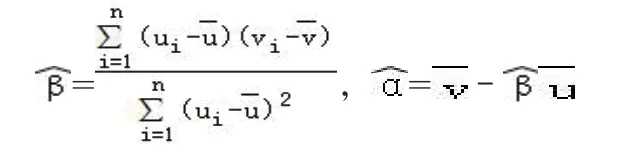
（Ⅱ）對于非線性擬合問題，先作出散點圖，再根據(jù)散點圖選擇合適的函數(shù)類型，設出回歸方程，利用換元法將非線性回歸方程化為線性回歸方程，求出樣本數(shù)據(jù)換元后的值，然后根據(jù)線性回歸方程的計算方法計算變換后的線性回歸方程系數(shù)，即可求出非線性回歸方程，關鍵在于換元的正確與否。

在第二問中，我們只需要找到對應變量進行換元，便可以輕松代入?yún)⒖紨?shù)據(jù)。因為題目和對應的公式間需要轉(zhuǎn)化的字母有四對，所以學生公式代入時會比較混亂。可以用圖示表達v=y，c=α，u=，β=d，這樣每一步轉(zhuǎn)化都會很清晰。