經歷建模之旅　感受數學魅力

林光明

摘要：《義務教育數學課程標準（2011年版）》指出：要想讓學生將數學和現實生活銜接在一起，就需要培養學生的模型思想，這是最基本的方法。教師要帶領學生設計數學模型，讓學生從現實生活中發現數學，通過空間模式和數量關系，掌握通過數學化語言設計成數學模型的各種技術和流程。

關鍵詞：數學模型;感受體驗;自主探究;數學魅力

《數學課程標準》指出：“數學要來自于生活，將學生現實生活作為素材設計成數學模型，進行數學知識的教學。”通過數學模型，可以更精準地進行數學知識的表達，讓師生和學生之間進行更高效的溝通交流，同時利用數學模型，還可以更高效地解決數學問題，指導學生發現數學的真諦。因此小學數學教師應該引導學生形成強烈的數學建模思想，根據現實問題設計數學模型，讓學生感受數學的魅力，更積極主動地通過數學思想和數學模型解決問題。

一、創設情境，初步感知數學模型

建模之前，需要分析模型關注的對象，分析存在大量相同特征的事物，將這些事物的特征總結出來，或者找出這些事物的關聯性，形成表象經驗。比如，教師先設計一個分橙子的情境，然后問學生，將十個橙子分給五個人，每個人有多少個？讓學生認識到除法的概念;然后提問學生，如果將這些橙子給兩個人，每個人可以得到幾個，讓學生根據這個提問列出公式，形成“平均分”的觀念;再次，將一個橙子分成兩半，提問學生，每份應該如何表達？讓學生意識到不夠分一個，該怎么辦呢？在這個時候學生便開始思考如何表達，教師可以引出“分數”的概念，告訴學生平均分成兩份，那么“2”便是分數中的分母，其中一份，便是分數中的分子，由此便形成基礎的分數模型。又通過具體的分東西情境，抽象到分數的意義。最后，要讓學生正確地描述分數的概念，聯系現實中的情況闡述分數的含義。

根據現實生活設計問題，可以讓更多的學生對數學知識產生好感，降低學生數學的學習難度，引導學生根據生活中積累的經驗分析，解決數學問題，感知數學模型的存在。

二、自主探究，主動建構數學模型

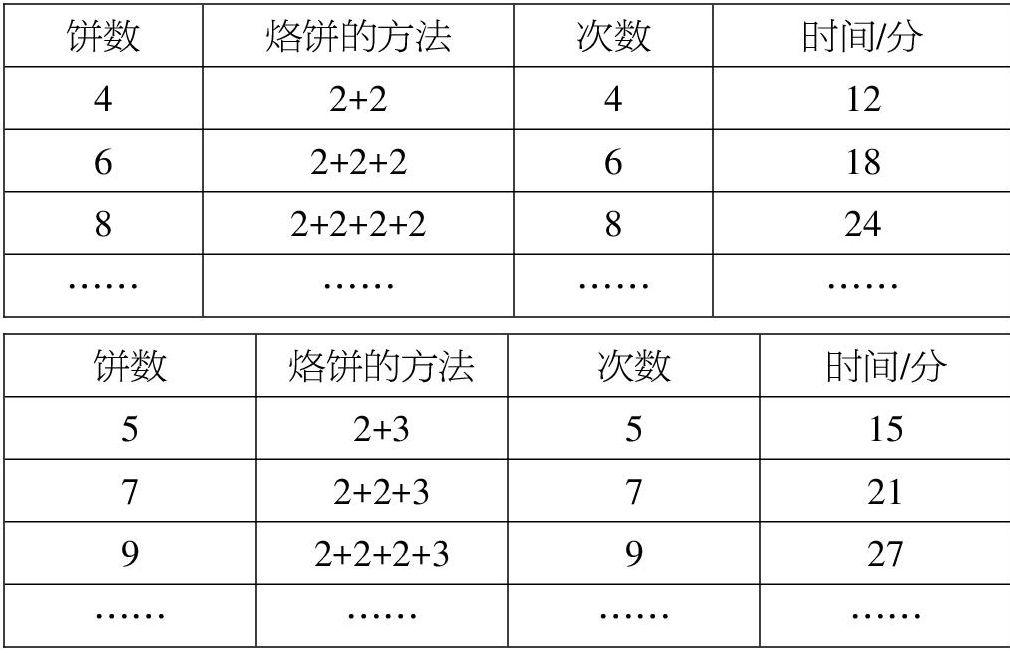
數學家華羅庚曾總結過：課本中的公式、定律等，在學習的過程中不僅僅是對公式和定律等本身進行學習，還應該分析這些公式和定律是如何形成的，對其進行探索和感受，才能夠真正認識這些公式和定律，才會更全面地學習數學知識，擁有數學智慧。比如在進行《烙餅問題》教學的時候，可以將數學模型的建立分成三個環節。第一，自主探索“烙2張餅至少需要多少時間？”烙2張餅學生在辨析中很容易明白：兩張餅一起烙，則六分鐘便可以完成，由此學生形成最基本的烙餅優化思想。“怎樣用最短的時間烙好3張餅？”對于學生來說是解決的重難點問題，在指導學生形成三張餅最優烙法的過程中，可以指導學生利用現有的資料進行操作，用課件等的方式，讓學生發現可以最大程度地使用鍋的空間，每次烙餅的時候，兩張餅在鍋里一起烙，便可以在最短的時間里完成。讓學生通過觀察進行思考，在動手的過程中進行總結，督促學生形成最基礎的運籌思想。第二，在沒有學具的幫助下，小組進行討論，分析雙數和單數張餅的情況下，最優烙餅的方式。

1.探究雙數個餅的烙法。

2.探究單數個餅的烙法。

在討論結果中，組織學生觀察數據尋找規律，在反饋交流時提煉出最優方法：總時間=餅數×烙一面餅的時間。學生從復雜到簡單的歷程，領略到自主探索后的欣喜。教師指導學生進行動手和探究與思考的時候，一方面可以進行策略性知識的灌輸，另一方面還可以帶領學生一起進行檢驗、探討、總結，進行數學思維的抽象和概括，讓學生在由淺入深的探究中，直觀地感受到數學模型建立的過程，形成了每個學生都能夠理解的簡單數學模型。

三、解決問題，拓展應用數學模型

通過設計數學模型和現實問題聯系在一起，讓學生真切地感受到數學模型的魅力，發現數學來自生活、服務于生活，認識數學的魅力，從而可以更顯著地強化學生的數學應用意識，提升學生通過數學模型解決現實問題的能力，在數學實際應用學習中感悟魅力、收獲知識、獲得快樂。比如在進行《乘法的初步認識》這節課教學中，教師可以將班級座位圖通過多媒體的方式展現給學生，讓學生計算班級中有多少人，先讓學生認識到乘法的概念，然后學會運用。教師可以講解：我們班里每個小組是6個人，一共是8個小組，這樣的情況下，便可以通過8×6或6×8的方法計算出來。學生在了解乘法概念后，設計出解決現實問題的乘法模型，將乘法模型和現實問題進行銜接，賦予乘法模型應有的應用價值。

另外在進行《植樹問題》課堂教學中，可以設置這樣的變式題：現在有一座樓，爬到4樓一共是48個臺階，假如每層樓的臺階數是一樣的，那么從1樓到6樓需要爬幾個臺階？學生在探索植樹問題之后，將植樹活動分成三種類型，在“把什么看作棵樹，什么看作間隔數”的引導中，學生便可以通過植樹問題中總結出來的規則和方法解決樓房的臺階問題，通過不同問題的銜接，讓學生可以通過數學模型處理相同類型的問題，體驗到數學模型的實用性。

四、結語

小學數學課堂中，將數學建模思想滲透課堂教學中，不僅可以使學生體會到數學并非只是一門抽象的學科，同時還能夠讓學生深刻認識到數學模型和現實問題是緊密銜接的，感受到數學模型的魅力，進而對數學產生更大的興趣。因此在數學課堂教學中，教師要用“活”教材，讓學生經歷數學建模之旅，感受數學的內在魅力，讓數學在學生心中大放異彩。

（責編 吳娟）