數學教學中的輾轉相除法
福建省福州第七中學 黃志鵬
一、歷史來源
輾轉相除法是目前仍然在使用的歷史最悠久的算法之一。它首次出現于幾何原本(卷7 命題1-2、卷10 命題2-3)(大約公元前300 年),而在中國則可以追溯至東漢出現的《九章算術》 。在卷7中用于整數,在卷10 中用于線段的長度(也就是現在所說的實數,但是當時未有實數的概念)。卷10 中出現的算法是幾何的,兩條線段a 和b 的最大公約數是準確測量a 和b 的最大長度。
二、簡介
在數學中,輾轉相除法又稱歐幾里得算法,是求最大公約數的算法。同時出現在高中教材人教A 版必修三第一章第四節。在教學中,輾轉相除法是算法教學的經典案例,我們有必要加深教師對該案例的理解,加強對于學生對數學的深入學習,提高對數學學科的學習熱情。因此,我們很有必要對輾轉相除法的原理及應用進行探索。
三、最大公約數的應用
1.最大公約數的定義
整數a1,a2,a3,…,an的公因數中最大的一個叫作最大公約數,記作(a1,a2,a3,…,an),若(a1,a2,a3,…,an)=1,我們則說a1,a2,a3,…,an互質或互素。
2.最大公約數的求解方法
例1:求20、30 和36 的最大公約數。解法一: 列舉法。
20 的因數有:1、2、4、5、10、20。
30 的因數有:1、2、3、5、6、10、15、30。
36 的因數有:1、2、3、4、6、9、12、18、36。
三個數的最大公約數是2。解法二:分解質因數的方法。
20=2×2×5,
30=2×5×3,
36=2×2×3×3,
(20,30,36)=2。解法三:短除的方法
(20,30,36)=2。
小結:在計算三個數的最大公約數的時候,要找三個數的公有的質因數,如果其中的兩個商還有質因數,也不要往下除。
例2:求18 和24 的最大公約數。
解:(1)用分解質因數的方法獨立完成。
(18,24)=2×3=6。
[18,24]=2×3×3×2×2=72。
(2)觀察發現:18×24=4×72。
小結:兩個自然數的最大公約數的一個重要性質是:兩個自然數的乘積等于這兩個自然數的最大公約數和最小公倍數的乘積。
延伸:若a、b 表示兩個自然數,則 a×b=(a,b)×[a,b]。
例3:兩個數的最大公約數是6,最小公倍數是504,如果其中的一個數是42,那么另一個數是多少?
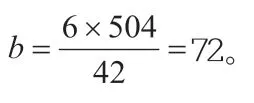
3.利用最大公因數解決實際問題
例4:有320 個蘋果,240 個橘子,200 個梨。用這些果品,最多可以分成多少份同樣的物?在每份禮物中,蘋果、橘子和梨各有多少個?
分析:根據題目的要求,在分禮物的時候必須正好分盡3 樣果品。因此,禮物的份數必須是320、240 和200 的公因數,現在還要求最多可以分成多少份同樣的禮物,也就是說要求320、240 和200 的最大公因數。
解:用短除法:
(320,240,200)=2×2×2×5=40。
因此,最多可以分成40 份,每份禮物中有蘋果320÷40=8(個),橘子240÷40=6(個),梨200÷40=5(個)。
四、輾轉相除法在解題中的應用
1.兩個有理數公因數的求法
2.兩個無理數公因數的求法
其中,a 為任意實數,甚至可以是多項式。
4.運用輾轉相除法把最大公約數表示為某量整數的倍數和
定理:若(a,b)=d,則必有二整數k、l 使得d=ka+lb。
例7:求一組整數x、y,使得150x+42y=(150,42)。
解:我們可以將輾轉相除過程寫成橫式(主要是在于應用歐拉演段):
得到6 為150 和42 的最大公約數,我們可將問題轉換為:求一組整數x,y 使得25x+7y=1。
這里我們應用歐拉演段解得該問題,求出所求兩數為2 和-7,歐拉演段就不在這里演示。
即6=150×2+42×(-7),于是x=2,y=-7 為所求。這也是輾轉相除法在代數解題中的小應用。
輾轉相除是后面才加入教材中的,是算法的經典案例,教學中注重這個內容的深入研究,是對于教學有促進作用的。放眼望去,輾轉相除法的應用極其廣泛,在各種計算機算法及編程中廣泛應用,特別地,在算法學習的研究中更是有著非常重要的地位。另外在高等數學中,它還被用來解丟番圖方程,尋找滿足中國剩余定理的數,或者求有限域中元素的逆。輾轉相除法還可以用來構造連分數,在施圖姆定理和一些整數分解算法中也有應用。輾轉相除法是現代數論中的基本工具。

