知其然知其所以然知其所以必然

朱錦云

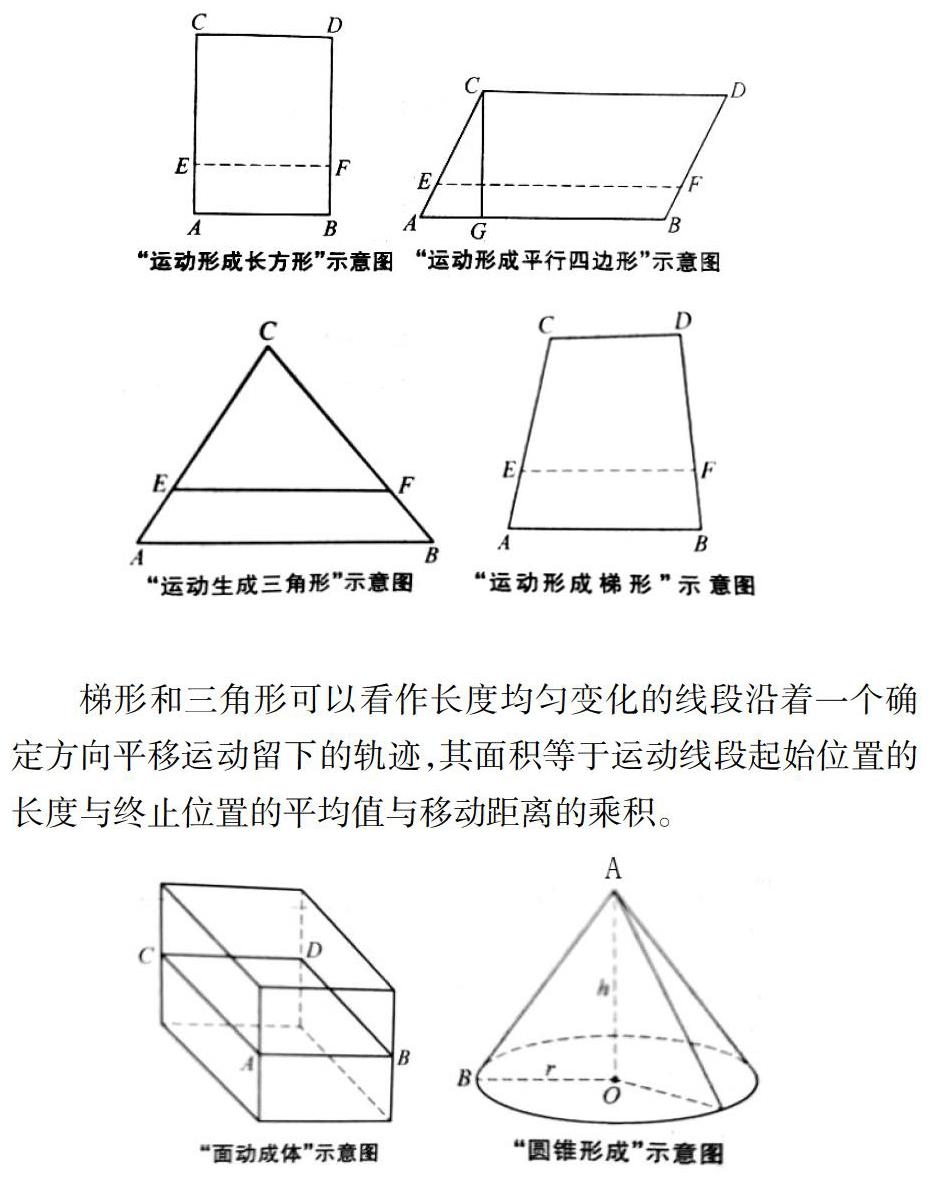
工作將近二十年，一直是大循環教學，總覺得自己對于小學數學知識已然了熟于胸。可讀完郜舒竹先生的《小學數學這樣教》之后，我開始陷入沉思。知其然，更應知其所以然，知其所以必然。這本書講述了許許多多被我們所忽略的“所以然”。正如郜先生所說，“所以然”的知識往往具有歷史性、貫通性、綜合性和人文性，是前人大師長期以來的結晶，是學生難以利用生活經驗通過自主或合作的方式探究出來的，是需要教師通過努力學習和研究并潛移默化地傳輸給學生的。因此，數學教學研究僅限于“如何教”和“如何學”這樣的問題是不夠的，還應重視“教什么”和“學什么”的研究，特別是對“所以然”知識的研究。

一、“所以然”之一：追根溯源，關注本質

知識感悟：追根溯源是一種刨根究底的學習方法，是探索知識的精神。追根溯源應從小學數學起始型概念知識入手，這是小學數學基礎知識的重要組成部分，也是發展學生思維、培養技能的基礎，在小學階段占據重要的地位。作為教師，我們應該弄清楚每一個概念的內涵和外延，以及概念之間的關系，不同的知識采取不一樣的方式，讓學生“知其所以然”。規律性知識，可以讓孩學生經歷自主創造的過程，從而感悟到“知識是因需要而產生的”;規定性知識，則通過接收性方式，讓學生明白這些規定的歷史隨機性和規定的合理性，要領會數學課程中“人為規定”的思想性。

比如加法的結果為什么叫做“和”，為什么不是“合”？……