淺談小學低年級數(shù)學《幾何直觀》畫圖教學策略

曾慶欣

數(shù)學是一門抽象、高度概括性的學科。對于思維相對簡單的小學生而言，要學好數(shù)學這門學科并不簡單。低年級的學生以形象思維為主，抽象思維能力較弱，作為“幾何直觀”教學的重要途徑之一——“畫圖策略”的地位就尤為重要。這種教學方法對教師教學和學生學習都有極大的幫助。

一、激發(fā)“畫”的意識，感知“幾何直觀”的優(yōu)越性

低年級學生思維較為簡單，對比較抽象的數(shù)量關系，或者條件更為復雜的題目，理解起來是有一定困難的。如低年級教材里面，經(jīng)常會看到類似這樣的題目，“小東前面有5人，后面有6人，這一行一共有多少人？”一開始，80%的學生都會列了5+6=11的算式，能正確解答的學生少之又少。可如果當你畫出這樣的一幅圖：

學生們一定會沖口而出，說出正確答案。

解決“比多少”的實際問題，一直是低年級學生學習的難點。誰和誰比，誰比誰多，誰比誰少難以分清，甚至一看到題目出現(xiàn)“比多”就加，“比少”就減的錯誤邏輯情況。曾做過一實驗，如教師只是出現(xiàn)文字信息：紅花有8朵，比黃花多3朵，黃花有多少朵？部分學生還是會用“5-3=2”來解答，因為他們分不清誰比較多，誰比較少。而若用圖示法：

再次讓學生回答誰比較多，誰比較少時，意見非常統(tǒng)一，全部正確。

通過純文字及圖示兩種方法的對比，學生能明顯感受到畫圖策略，利用幾何直觀的好處。同時，教師亦可順勢引導，可以通過圓圈、三角形、其他符號等去表現(xiàn)人或事物。

二、掌握“畫”的方法，為運用“幾何直觀”提供保障

“畫”的方法不是與生俱來的，幾何直觀教學也必須是一個長久的過程。在一年級的學習中，學生在教材與學習過程中已初步感知到，可以用小圓片等表示具體物體的數(shù)量，如：5個蘋果，可以用5個小圓形表示，進而再抽象出可以用數(shù)字“5”來表示。當然，想學生學會用線段去表示“5”，直接告知，并不是最好的方法。在解決問題的過程中產(chǎn)生沖突，進而想方法解決才是最優(yōu)的。如，可以用5個小圓形表示數(shù)字“5”，那怎么去表示“50”呢？當然，還是會有學生提出用50個小圓形來表示，教師可以讓其上來黑板畫;另外再詢問還有沒有其他的方法，由聰明的學生或教師介紹畫線段的方法。只需要在畫上一條小橫線，上面標上“50”，就可以代表“50”了。而此時，剛才提議畫小圓形的學生還在黑板上畫，強烈的對比，讓學生顯而易見地感受到，有時候用線段比畫圖形來得更簡便。教師繼而發(fā)問：“這是一條表示50的線段，那如果表示30，用線段怎么表示？40呢？100呢？”同時，教師在日常教學中，也可繼續(xù)介紹大括號、集合圈等符號的作用。

在潛移默化的滲透過程中，學生便漸漸掌握了“畫”的方法，為以后運用“幾何直觀”解決問題提供了保障。

三、激發(fā)“畫”的興趣，規(guī)范“幾何直觀”的表達

當然，畫圖的策略對于低年級學生來說，沒有唯一性，教師只是起到了示范、啟發(fā)與指導的作用。

在課堂上，鼓勵學生用自己喜歡的方式畫圖，激發(fā)學生畫圖的興趣，并抓住教學契機讓學生展示自己的作品，說出自己的想法，及時對學生進行表揚鼓勵，激發(fā)學生運用畫圖策略的熱情。并采取了一系列的措施，來激發(fā)學生的畫圖興趣：比如上課時讓學生在黑板上畫圖，然后師生共同評析，看哪個同學畫得好，優(yōu)點在哪里，存在哪些毛病;印發(fā)常見的基本直觀圖給學生，讓學生反復觀摩，然后再畫出來;數(shù)學活動課中還組織學生進行“畫直觀圖比賽”。這些措施激發(fā)了學生的學習興趣，使學生認識到規(guī)范作圖的重要性，增強了學生的畫圖能力。

學生愛“畫”還要會“畫”，教師要規(guī)范學生的畫圖習慣。首先，通過多種途徑和方式，使學生真正體會畫圖對理解概念、尋求解決思路帶來的益處。其次，要求學生解決問題時能畫圖的盡量畫圖，將相對抽象的思考對象“圖形化”，盡量把數(shù)學的過程變得直觀，直觀了就容易展開形象思維。再次，要讓學生規(guī)范畫圖，能準確直觀的表達題意。

四、培養(yǎng)“畫”的意識，提升“幾何直觀”解決問題的素養(yǎng)

將幾何直觀用于描述和分析“非幾何與圖形”領域的問題時，恰恰最能彰顯幾何直觀的價值。這樣教學，能更好地培養(yǎng)學生的幾何直觀意識與能力，最終提升幾何直觀素養(yǎng)。

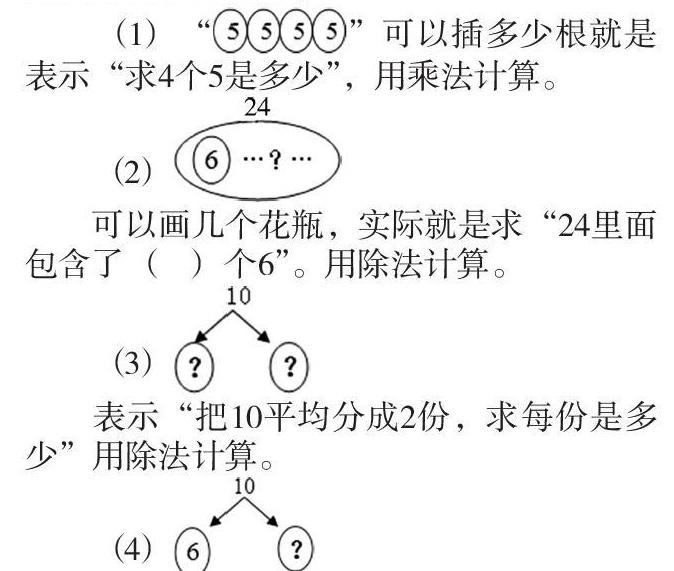
教學二年級《表內除法》這一單元時，學生常常會對信息復雜而又相近的題目無所適從。如書本第27頁第4題，這是一道綜合性非常強的一道題。（1）每個花瓶插5根羽孔雀毛，4個花瓶可以插多少根？（2）每個花瓶插6根孔雀羽毛，24根孔雀羽毛可以插幾個花瓶？（3）有10根孔雀羽毛，平均插在2個花瓶里，每個花瓶插幾根？（4）有10根孔雀羽毛，插在2個花瓶里，一個花瓶插6根，另一個花瓶里插幾根？

在集備時，教師們對此內容進行過探討，方法各異：一種是認為要教給學生數(shù)量關系式，如：每份數(shù)×份數(shù)=總數(shù);總數(shù)÷份數(shù)=每份數(shù);總數(shù)-部分數(shù)=部分數(shù)……依據(jù)這樣的關系式子，讓學生去“分析”，去“用”，好比建筑工地的腳手架。但是，從學生們一臉茫然的表情中，我們得知，套用公式的做法并不能讓學生真正理解算理。另一種聲音就是靠“多說”，教師示范學生跟說，多說幾次學生就能理解了。可是，這樣做，忽視了“理解不是建立在說之上，而是會說應該建立在理解之上”。還有一種就是，“讓學生畫圖理解”。拿到題目，可以邊讀邊根據(jù)題意畫出草圖，根據(jù)草圖再一次理解題意，然后尋求解決問題的辦法。

如剛才的4小題我們可以通過這樣的直觀圖幫助學生理解：

經(jīng)過一段時間的訓練，我們發(fā)現(xiàn)，學生若能畫出草圖，對題目的意思也就理解相當正確了，在解決問題列式時也就顯得頗有頭緒了。

總之，“畫”在探究數(shù)學知識中確實藏有博大精深的奧妙。畫圖策略與幾何直觀有著千絲萬縷的關系。借助畫圖教學，可以培養(yǎng)和發(fā)展學生的幾何直觀能力，感悟初步的數(shù)形結合思想。重要的是，學生能通過畫圖將復雜的數(shù)學問題變得簡明、形象，以便更快地找到解決問題的方法。發(fā)展好學生的圖形語言，培養(yǎng)幾何直觀能力，能為后續(xù)更好地學習較復雜的幾何知識打下良好的基礎。