一道高考解析幾何題的再探究

浙江省金華市第六中學 (321000) 虞 懿

1.考題展示

(2019年高考浙江卷第21題)如圖1所示，已知點F(1,0)為拋物線y2=2px(p>0)的焦點．過點F的直線交拋物線于A,B兩點，點C在拋物線上，使得△ABC的重心G在x軸上，直線AC交x軸于點Q，且點Q在點F右側．記△AFG，△CQG的面積分別為S1,S2．

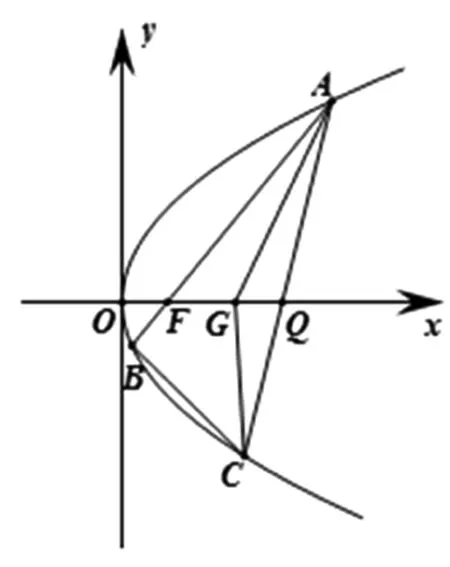
圖1

(Ⅰ)求p的值及拋物線的準線方程；

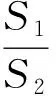
分析：本題以拋物線為載體，主要考查拋物線的幾何性質、直線與拋物線的位置關系、重心與面積等基礎知識，同時考查解析幾何的基本思想方法和綜合解題能力．本題設計新穎，構思巧妙，耐人尋味，令人賞心悅目，體現了“能力立意”的指導思想，凸顯了數學試題的選拔功能．

由于問題(Ⅰ)較為簡單，本文不作討論，下面僅對問題(Ⅱ)進行探究．

2.解法優化

優解1：借助重心性質，實現面積比的代數表示

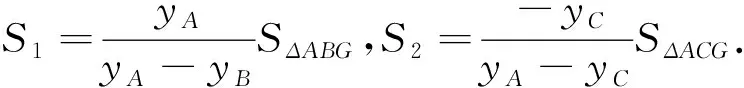
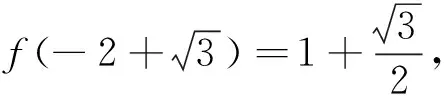
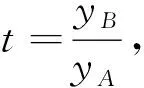
優解2：回歸向量本質，實現面積比的代數表示

向量具有代數、幾何雙重身份，融數形于一體，是溝通代數和幾何的橋梁．它可以將幾何問題坐標化、數量化，因此它也是解決解析幾何問題的重要工具．

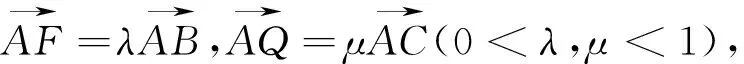
評注：在探究解題思路時，要善于從不同的角度分析、挖掘它與其他知識的聯系，在平面解析幾何中涉及長度、面積(比)、角度的計算及有關平行、三點共線、垂直等位置關系問題時，都可以利用向量知識加以解決．

3.多向拓廣

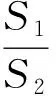
拋物線與橢圓、雙曲線“同宗同源”，那么橢圓、雙曲線是否具有上述類似結論成立？回答仍是肯定的．

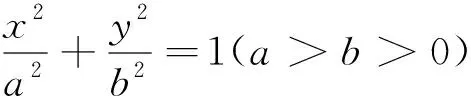
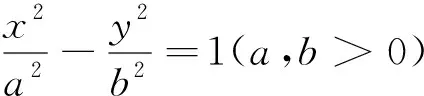
4.本源探究

燕尾定理：如圖2所示，在ΔABC中，AD,BE,CF相交于同一點O，那么SΔAOB:SΔAOC=BD:CD．

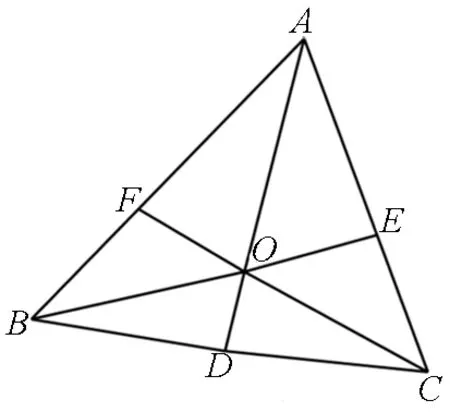
圖2

燕尾定理給出了一個轉化面積比與線段比的手段，因為ΔAOB和ΔAOC合起來的圖形的形狀很象燕子的尾巴，所以這個定理被稱為燕尾定理．該定理在許多幾何題目中都有著廣泛的運用，它為三角形面積比與對應底邊比提供了互相聯系的途徑．

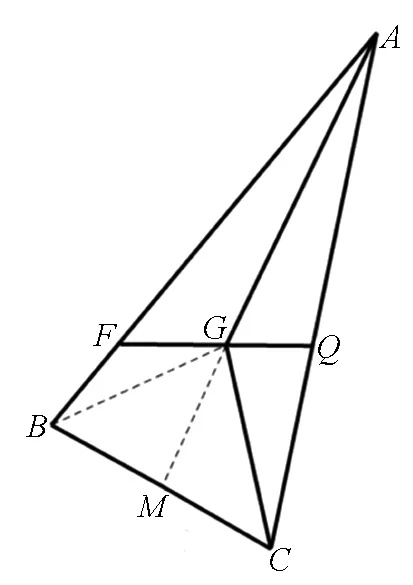
圖3

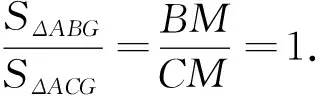
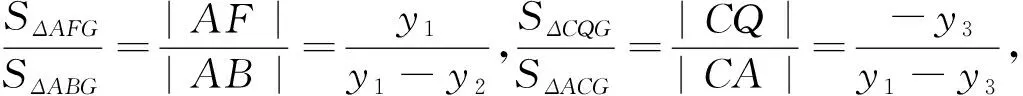
評注：可以看出，拓廣4是考題的命題本質，高考試題將這個本質放在圓錐曲線中，賦予更豐富的圖形與知識，進而考查直線與圓錐曲線的相關內容，考查學生的轉化與化歸，數形結合等思想與能力．(拓廣1～3的證明，仿上述證法即可．)

事實上，解析幾何問題的本質仍是幾何問題，解題時要充分把握解析幾何中圖形的特征，緊扣其中關鍵的幾何要素，挖掘圖形相應的幾何性質，恰當地運用平面幾何的相關知識，將解析法與平面幾何方法相結合，往往能簡化運算，優化解題過程，能起到四兩撥千斤的功效．

5.變式提升

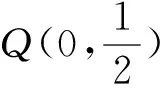
變式2 如圖4所示，過拋物線y2=2px(p>0)上一點P作拋物線的切線l交x軸于Q，F為焦點，以原點O為圓心的圓與直線l相切于點M．

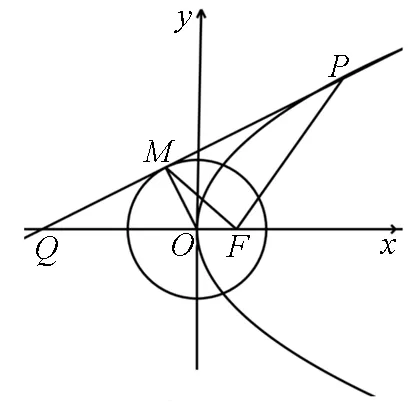
圖4

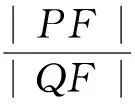
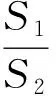
解題是一種創造性活動，作為數學的學習，積累一定的解題經驗對以后解題過程中快速提取信息應該是幫助很大的，而有針對性地進行變式訓練，則是解題經驗自覺積累的有效途徑．如在完成上面的高考問題探究后，若我們能從結論或條件的適當變化中編擬出一些問題，就可以鞏固方法，辨析異同，提升能力．

對高考試題的再探究，不僅能使教師清晰地理解命題人的思想、命題背景和考查目的，還可以更好地培養學生思維品質，提高學生提出問題、分析問題和解決問題的能力，提高學生的數學核心素養．