初中生幾何證明中邏輯推理錯誤及對教學(xué)的啟示探析

侯肖玲

【摘 要】在核心素養(yǎng)背景下，對初中數(shù)學(xué)教學(xué)的要求越來越高，教師不僅要教授學(xué)生基礎(chǔ)的數(shù)學(xué)知識，更要注重對學(xué)生的數(shù)學(xué)邏輯推理能力的培養(yǎng)，從而有效落實數(shù)學(xué)核心素養(yǎng)的培養(yǎng)目標(biāo)。在初中數(shù)學(xué)中，幾何證明題可以較好地鍛煉學(xué)生的邏輯推理能力。本文以三角形內(nèi)角和定理的證明為例，分析了在初中幾何證明中學(xué)生容易出現(xiàn)的邏輯推理錯誤，并總結(jié)了相關(guān)的教學(xué)經(jīng)驗。

【關(guān)鍵詞】初中;幾何證明;邏輯推理錯誤;教學(xué)啟示

【中圖分類號】G633.6 ?【文獻標(biāo)識碼】A ?【文章編號】1671-8437（2020）16-0173-02

初中階段正是學(xué)生的思維方式、行為習(xí)慣和價值觀念形成的關(guān)鍵時期。但數(shù)學(xué)理論本身具備一定的抽象性和嚴(yán)謹(jǐn)性，對學(xué)生邏輯思維有較高的要求，所以教師需要利用一定的教學(xué)手段提高學(xué)生的邏輯推理能力。

1 ? 初中生幾何證明中的邏輯推理錯誤分析

1.1 ?循環(huán)論證

初中生的邏輯思維還不夠成熟，對數(shù)學(xué)問題的理解仍然處于形象思維階段，所以在幾何證明中，學(xué)生時常會出現(xiàn)循環(huán)論證的情況。循環(huán)論證可以理解為在證明時，要證明結(jié)論的論據(jù)本身，則需要通過要證的結(jié)論才可以實現(xiàn)。如下面的錯誤證明情況。

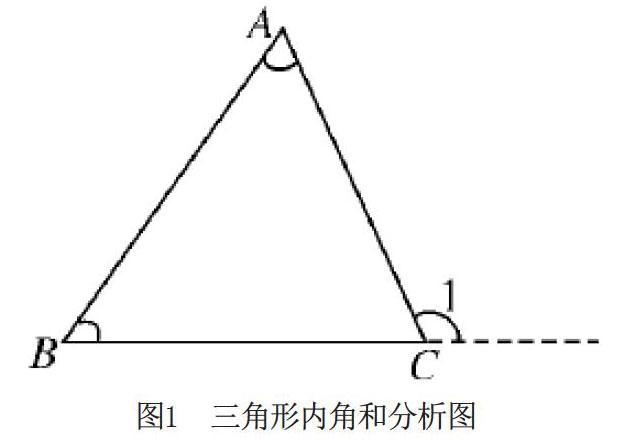
如圖1所示，在△ABC中，沿著BC邊向C的方向作延長線，那么∠1就是∠A+∠B的和，此情況可以總結(jié)為在三角形中一個外角等于與它不相鄰的兩個內(nèi)角之和。就此得出三角形內(nèi)角和定理，即由于∠ACB與∠1的和為180°，所以∠A+∠B+∠ACB=180°，也就是三角形內(nèi)角和為180°[1]。

此種循環(huán)論證的方式在學(xué)生論證過程中很容易出現(xiàn)。證明時，學(xué)生會將三角形內(nèi)角和定理作為推理根據(jù)。但是從湘教版初中數(shù)學(xué)教材編排情況來看，運用此定理進行證明并不合理，因為此定理是經(jīng)過一系列證明后得出的，而學(xué)生將它直接運用到證明中，顯然是不符合邏輯的，所以不能用∠ACB與∠1的和為180°來證明三角形內(nèi)角和定理。

1.2 ?偷換概念

學(xué)生在幾何論證過程中會使用另外一個概念替換問題中的某些概念，使得問題概念的具體內(nèi)涵發(fā)生改變。如結(jié)合等邊三角形的性質(zhì)得出∠A=∠B=∠C=60°，所以∠A+∠B+∠C=180°，最終得出三角形內(nèi)角和為180°。該證明選用的等邊三角形屬于特殊類三角形，使用此類三角形進行推理，就混淆了一般和特殊的關(guān)系，這是較為典型的邏輯推理錯誤。

2 ? 對初中幾何證明教學(xué)的啟示

2.1 ?強化學(xué)生對公理化方法的理解

只有在同一個公理體系中進行證明，才可以判斷幾何證明中的邏輯推理是否正確，否則很容易出現(xiàn)錯誤。如對于三角形內(nèi)角和定理，在證明過程中，需要先利用平行線具有的性質(zhì)論證觀點，然后在此基礎(chǔ)上得到三角形內(nèi)角和為180°。從這一公理系統(tǒng)看，是可以使用上述方法證明三角形內(nèi)角和定理，但從初中數(shù)學(xué)教科書的公理系統(tǒng)看，使用此種邏輯就會出現(xiàn)循環(huán)論證的誤證。因此，初中數(shù)學(xué)教師需要從教學(xué)的本質(zhì)出發(fā)，更細(xì)致地講解平面幾何的公理體系，讓學(xué)生更好地感受幾何的邏輯美，體會邏輯推理的強大力量[3]。

2.2 ?靈活利用思維導(dǎo)圖，明確命題邏輯關(guān)系

平面幾何具有較強的邏輯性，可以提升學(xué)生的邏輯推理能力。從新課程改革看，初中數(shù)學(xué)教科書在難度編排上主要呈現(xiàn)螺旋式的上升狀態(tài)。這樣的過渡能促使學(xué)生思維逐步由感性認(rèn)知向理性認(rèn)知轉(zhuǎn)變。而為了更好地提高學(xué)生的邏輯推理能力，教師可以為學(xué)生設(shè)立核心問題，而后引導(dǎo)學(xué)生圍繞核心問題將相關(guān)內(nèi)容通過思維導(dǎo)圖畫出來。這樣不僅有助于幫助學(xué)生構(gòu)建新的知識網(wǎng)絡(luò)，完善學(xué)生的知識體系，同時也可以使學(xué)生更好地將新舊知識相連接，有效理清知識之間的邏輯關(guān)系，增加邏輯推理能力。

2.3 ?引導(dǎo)學(xué)生分辨特殊和一般

學(xué)生會因在幾何證明中混淆了特殊和一般的關(guān)系而導(dǎo)致錯誤。如在證明三角形內(nèi)角和定理時，使用特殊三角形——等邊三角形并不能完全證明結(jié)論;而在推理過程中，利用矩形推導(dǎo)三角形內(nèi)角和定理，也忽視了四邊形、多邊形體現(xiàn)出來的性質(zhì)。因此，教師在實際教學(xué)中需要正確引導(dǎo)學(xué)生分析特殊與一般的關(guān)系，使學(xué)生進一步探索規(guī)律，找到更加合適的解決問題的方法。此外，特殊化處理后，教師還需要引導(dǎo)學(xué)生將結(jié)論或方法推廣到一般中去。

總之，在初中幾何證明教學(xué)中，教師需要讓學(xué)生懂得探究特殊問題的目的在于發(fā)現(xiàn)規(guī)律，弄清特殊和一般的關(guān)系，并學(xué)會靈活轉(zhuǎn)換到問題的解決中，從而培養(yǎng)學(xué)生的邏輯推理能力，提升學(xué)生的數(shù)學(xué)思維。

【參考文獻】

[1]馬維俊.初中幾何證明分析方法簡析[J].課程教育研究，2020（2）.

[2]黃喆，陳飛，梁珍，陳永明.幾何證明——初中數(shù)學(xué)分叉點研究之三[J].數(shù)學(xué)教學(xué)，2019（10）.

[3]秦曉.例談初中幾何證明中“輔助線的自然生成”[J].數(shù)學(xué)教學(xué)通訊，2019（11）.