例談如何實現數學學習的“深一度”
尹文軍
(南京市浦口區行知小學,江蘇南京,210000)
深度學習是源于人工智能網絡的一個概念,后被教育工作者引入教育教學,一般指在真實復雜的情境中,學生運用所學的知識和技能,對信息進行深度加工,深刻理解和掌握復雜概念的內在含義,并主動建構知識體系,進而以知識遷移推進實際問題解決的學習過程、狀態和結果。[1-2]在教學中,為實現學生數學學習的“深一度”,教師需要超越表層的符號教學,[3]對學習材料、學習路徑、學習狀態做深入細致的思考和探究。
一、研究學習材料的數學本質,實現本質的“深一度”
什么是數學本質?不同角度的分析可能會有不一樣的理解。不少學者認為,數學的本質就是探索和研究數學所依賴的那些基本思想,也就是“將具體的數學知識都忘掉以后剩下的東西”,主要包括數學抽象的思想、數學推理的思想和數學建模的思想。最近,也有學者基于數學史的沿革,提出數學本質就藏在數學演變的線索中,那些一直保留的并且不斷建構和延展的數學內容,理應就是數學的本質。此話說起來簡單,但尋找起來卻不是一件容易的事。
要想對“什么是數學的本質”給出一個清晰的、公認的表達,并不是一件容易的事情。問題是一線教師應該怎樣凸顯相關內容的數學本質,進而有效落實培養學生數學核心素養的改革目標。筆者認為,天下大事必作于細,天下難事必作于易,教師應該從熟悉的教材和課堂入手開展實踐和思考。
“認識面積”是小學數學“圖形與幾何”領域的重要內容。面積的本質是什么?在古代,為了確定農業收成、計算稅收,必須丈量土地,由此產生了面積的概念。中國古代形象地用“冪”或“積”來表示面積。其中,“冪”指遮蓋物品的方形布,“積”指積累。因此,面積的本質是“面的積累”。小面積大面,是物體表面的本質屬性,非比較出來的大小,而是積累起來的“多少”。更重要的是,“冪”是測量面積的標準,即單位。所以,人類對面積的認識源于測量。
基于對面積本質的認識,教師在設計教學時組織學生進行以下測量活動:(1)用鉛筆盒的面測量書本面,說說書本的面里大約有幾個鉛筆盒的面;(2)用書本的面測量課桌的面,說說一張課桌面里大約有幾個書本面;(3)觀察并說說黑板的面大約有幾個課桌的面;(4)用規定大小的紙片測量一張A4紙的大小。通過多個測量任務,學生運用了不同的標準進行測量,在此過程中感受到面積源于對物體表面的測量,測量面積要有一定的標準,面積的大小是指大面積里含有多少個小面積等本質含義。測量活動促進了學生對數學知識本質的深度認識。
二、適時追問核心問題,實現過程的“深一度”
估算是小學數學教學中的一個重點和難點。在第一學段,《義務教育數學課程標準(2011年版)》將“能結合具體情境,選擇適當的單位”作為估算的核心。在人教版三年級“用估算解決實際問題”中有這樣一道例題:“每張門票8元,29位同學參觀,帶250元夠不夠?92位同學參觀,帶700元夠不夠?帶800元呢?”在解決此題的過程中,學生會用“30”和“90”分別作為“29位同學”和“92位同學”估算的單位,其估算的結果是可靠的。但是,在解決“800元夠不夠”的問題時,大多數學生仍然以“90人”為單位進行估算,很少有學生想到用“100人”作估算單位。這種情況下,教師可適時追問兩個問題:(1)以“90人”為單位進行估算,其估算結果可靠嗎?(2)由“帶800元”和“每張門票8元”這兩個條件,你還能想到什么?通過追問,教師啟發學生可以用“100人”做單位進行估算,學生比較之后發現,其估算結果比以“90人”為單位進行估算更可靠。
三、追求數學知識結構化認識,實現認識的“深一度”
平移是物體運動的一種形式。在蘇教版四年級下冊“圖形的平移”中,教師一般通過數格子的方式讓學生體會運動的方向、距離以及圖形平移前后的大小、形狀及位置關系。在這樣的教學中,學生對平移的認識往往是零碎的。為了幫助學生建構結構化的知識體系,教師可以嘗試以下學習任務:(1)畫,畫出金魚圖平移的路線;(2)數,金魚圖向( )平移( )格。該任務具有一定的開放性,學生可以采用不同的方式進行探索、解答,呈現出多種不同的畫法和數法,如圖1—圖3。

圖1 生1

圖2 生2

圖3 生3
在學生交流平移想法之后,教師可以把學生的幾幅平移路線放在同一張圖上,幫助學生通過觀察、比較、分析,提煉出平移運動的元素和特征,如圖4所示。

圖4 平移運動的元素和特征
從圖4可知,以平移的路線為核心,學生動態地認識了平移的本質:一個圖形和它經過平移所得的圖形中,兩組對應點的連線平行且相等。
四、尋求關聯、溝通的數學方法,實現方法的“深一度”
數學方法是數學思維的具體體現。由于思維方式和思維能力的差異,在解決具體數學問題時,學生采用的方法也不盡相同。以人教版四年級“雞兔同籠”問題為例。“籠子里有若干只雞和兔。從上面數,有8個頭,從下面數,有26只腳。雞和兔各有幾只?”為了解決這個問題,學生采用了多種方法,其中,比較典型的有畫圖法、列表法、直接計算法等。
生1:我是畫圖的,我先畫8個頭,每個先畫兩只腳,再一個一個添上兩只,邊畫邊數,數到26只,發現雞有3只,兔有5只。
生2:我是列表的,從雞有8只,兔有0只開始,一個一個推算出雞有3只,兔有5只。
生3:我是列式計算的,如果都是雞,就有8×2=16只,……
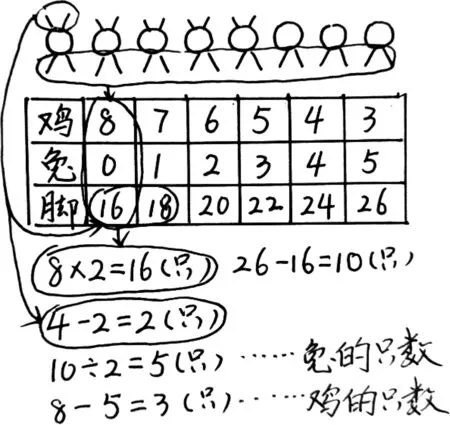
圖5 解題思路
當學生匯報完各自的想法后,教師對這幾種想法進行關聯和溝通,繪制出如圖5的解題思路。通過關聯,學生意識到,雖然表達形式不同,但它們的共同點都是先假設這8只全是同一種動物(雞或兔),再根據題中條件進行調整。如此,學生對方法的認識得到升華,思維得以進階。
五、進行有效的容錯、化錯,實現思維“深一度”
基于小學生的認知特點,在帶著問題和任務自主探索的過程中,學生會出現多種既有共性又有個性的結果,也會經常出現錯誤的結果。對于錯誤的結果,教師更多的應應是包容和合理利用。蘇教版五年級上冊“小數乘小數”的計算一課中,學生計算3.8×3.2時出現了下面兩種典型錯誤:

圖6 學會繪制的解題圖形
錯誤1:

錯誤2:
3.8×3.2=9.16(平方米)
此時,教師不必急于判斷對錯,而是放手讓學生嘗試用不同的方法畫一畫、算一算房間的面積。在此過程中,部分學生畫出了如圖6的圖形。“像上面的算法,哪幾塊面積沒有算出來呢?”通過畫、質疑、爭辯、解釋,教師讓學生明晰錯誤,進而真正理解小數乘法的算理。

