基于“問題意識”的創(chuàng)新能力培養(yǎng)策略

顧桂萍 黃錦

[摘? 要] 問題是思維的動力，是創(chuàng)新的基石. 筆者將問題意識這一維度作為一個實(shí)踐視角，分析學(xué)生在問題意識這一方面的表現(xiàn)，以期培養(yǎng)學(xué)生的創(chuàng)新能力，為全面提升教學(xué)質(zhì)量提供支持.

[關(guān)鍵詞] 問題意識;創(chuàng)新能力;培養(yǎng)

隨著時代的發(fā)展，教育領(lǐng)域?qū)?chuàng)新能力的重視程度日益攀升，創(chuàng)新能力成為數(shù)學(xué)教育研究和實(shí)踐領(lǐng)域的熱點(diǎn)概念. 學(xué)術(shù)界對創(chuàng)新能力相關(guān)的討論也非常廣泛，逐步將人們對創(chuàng)新能力的理解引向深處.

著名數(shù)學(xué)家丁石孫曾說：“沒有問題的學(xué)生不能算好學(xué)生. ”問題是創(chuàng)新的基石，培養(yǎng)學(xué)生的問題意識是促進(jìn)他們創(chuàng)新意識的好方法，是創(chuàng)新能力得以升華的有效途徑. 在實(shí)際學(xué)習(xí)中，學(xué)生的問題意識處于怎樣的水平？問題意識如此重要，為何學(xué)生提出問題的能力總不能讓教師滿意呢？該如何加以訓(xùn)練才能提升他們的創(chuàng)新意識呢？為了回答這些問題，筆者將問題意識這一維度作為一個實(shí)踐視角，分析學(xué)生在問題意識方面的表現(xiàn)，以期培養(yǎng)學(xué)生的創(chuàng)新能力，為全面提升教學(xué)質(zhì)量提供支持.

以“問題情境”引問，能激起創(chuàng)新意識的內(nèi)在活力

數(shù)學(xué)知識的特點(diǎn)決定了數(shù)學(xué)教學(xué)的重要方式是問題引領(lǐng)學(xué)生探究，激起學(xué)生的質(zhì)疑問難. 這就要求教師在課堂中關(guān)注學(xué)生對問題的思考與研究. 然當(dāng)前的教學(xué)實(shí)踐中，很多時候?qū)W生就是在教師所設(shè)計(jì)的程序活動中機(jī)械學(xué)習(xí)，被動完成教學(xué)任務(wù)，毫無疑問，毫無發(fā)現(xiàn)，毫無思維的參與，這樣的學(xué)習(xí)過程是低效的，是一種“偽學(xué)習(xí)”. 只有精心設(shè)計(jì)問題情境，以個性化的問題引領(lǐng)，才能使學(xué)生在思想上自覺生成疑問，從而激起創(chuàng)新意識的內(nèi)在活力.

案例1？搖 以“實(shí)數(shù)”的課堂導(dǎo)入為例.

筆者通過以下情境進(jìn)行課堂導(dǎo)入：隨著時代的變化和社會的不斷發(fā)展，人類一刻都沒有停止過前進(jìn)的腳步. 同學(xué)們，天上飛的飛機(jī)，水里航行的輪船，宇宙中探月的飛船，天空中升起的火箭……它們的位置是怎樣變化的呢？我們該如何確定它們變化著的位置？

設(shè)計(jì)意圖？搖 以上案例中，教師以學(xué)生喜聞樂見的生活情境為素材，激起學(xué)生探求知識的欲望，點(diǎn)燃他們學(xué)習(xí)數(shù)學(xué)的熱情，使其快速投入數(shù)學(xué)思考之中，引發(fā)學(xué)生質(zhì)疑：為什么要學(xué)習(xí)這一章節(jié)的知識呢？這一章節(jié)的學(xué)習(xí)有何意義？就這樣，學(xué)生從中充分感受到了數(shù)學(xué)的應(yīng)用價(jià)值，并在充足的自主思考空間中發(fā)現(xiàn)問題和提出問題，激起數(shù)學(xué)思考意識，培養(yǎng)創(chuàng)新精神.

以“問題”驅(qū)動學(xué)生的發(fā)現(xiàn)，以“發(fā)現(xiàn)”激起學(xué)生的質(zhì)疑，以“質(zhì)疑”推動學(xué)生思維的發(fā)展. 教師唯有創(chuàng)設(shè)精巧的問題情境，并做到以生為本，才能激起學(xué)生探究的內(nèi)驅(qū)力，使學(xué)生在這樣的生態(tài)課堂中打開自身的“問題閘門”，盡情地展開想象和思維的翅膀，綻放創(chuàng)新思維的光芒.

以“開放性問題”導(dǎo)問，是培養(yǎng)?創(chuàng)新意識的外在助力

傳統(tǒng)數(shù)學(xué)教學(xué)過于關(guān)注知識的傳授，總是忽視知識的發(fā)生、形成和應(yīng)用，無法較好地將數(shù)學(xué)知識中蘊(yùn)含的思想方法和創(chuàng)造力暴露出來，即便是應(yīng)用也僅僅是一題一解的形式. 在這樣的教學(xué)模式下，學(xué)生易固化學(xué)習(xí)形式，只會聽講與模仿;在這樣的課堂教學(xué)下，學(xué)生將淪為學(xué)習(xí)的機(jī)器，談何問題意識？談何創(chuàng)新意識？

伴隨著素質(zhì)教育的推進(jìn)，不少教師逐漸認(rèn)識到數(shù)學(xué)教學(xué)的本質(zhì)，并開始注重培養(yǎng)學(xué)生的問題意識與質(zhì)疑習(xí)慣. 從開放性問題著手導(dǎo)問，讓學(xué)生在思考與實(shí)踐的過程中自然地提出問題，進(jìn)而形成相應(yīng)的創(chuàng)新能力，是素質(zhì)教育賦予數(shù)學(xué)教學(xué)的主要任務(wù). 因此，教師需要嘗試挖掘教材中一些典型的例題、習(xí)題，將其打磨為開放性問題，讓學(xué)生去思考、去探究，真正“卷入”探究活動之中，培養(yǎng)創(chuàng)新能力.

案例2？搖 全等三角形.

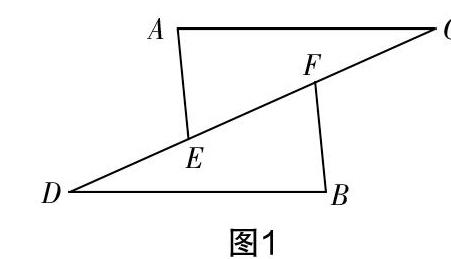
例題：如圖1，E，F(xiàn)兩點(diǎn)在CD上，AE=BF，CE=DF，且AE∥BF. 證明：△AEC≌△BFD.

此題為教材中的一道典型例題，為了給學(xué)生創(chuàng)造更為廣闊的思維空間，筆者進(jìn)行了如下改編.

問題1：如圖1，E，F(xiàn)兩點(diǎn)在CD上，AE=BF，CE=DF，? ? ? ? ? ?. 證明：△AEC≌△BFD.

（請?jiān)囍跈M線上添上一個適當(dāng)?shù)臈l件，使△AEC≌△BFD成立，并予以證明）

問題2：如圖1，E，F(xiàn)兩點(diǎn)在CD上，AE=BF，CE=DF，且AE∥BF. 你可以得出什么結(jié)論？并加以證明.

對于問題1，學(xué)生通過獨(dú)立思考和自主探究，可以填出以下答案：①AC=DB;②AE∥BF;③∠AEC=∠BFD. 并一一予以證明. 對于問題2，學(xué)生除去思考得出例題中的“△AEC≌△BFD”之外，還得出了以下結(jié)論：①AC=BD;②DE=FC;③∠C=∠D;④∠A=∠B;⑤AC∥BD等.

設(shè)計(jì)意圖？搖 在案例2中，教師從學(xué)生思維的最近發(fā)展區(qū)創(chuàng)設(shè)開放性問題，給予每個學(xué)生參與探究的機(jī)會，讓學(xué)生可以根據(jù)自身的知識與能力水平提出問題和解決問題，使每個學(xué)生都有獲得成功的機(jī)會. 這樣的訓(xùn)練，能讓他們在參與中質(zhì)疑，在質(zhì)疑中不斷發(fā)展，能有效訓(xùn)練學(xué)生的發(fā)散思維與求異思維，能使創(chuàng)新思維得到深化. 對學(xué)生而言，解決開放性問題的過程不僅是一種學(xué)習(xí)力生長的展現(xiàn)，更是一種創(chuàng)造的過程，他們從中獲取的不僅僅是這樣一道習(xí)題，更是一種創(chuàng)新意識和精神.

教師緊緊把握新課程開放的特征精心設(shè)計(jì)的開放性問題，不僅能使學(xué)生真正變被動思考為主動探究，還能激發(fā)學(xué)生的問題意識，能有力地促進(jìn)學(xué)生探究能力和創(chuàng)新能力的發(fā)展，使學(xué)生適應(yīng)素質(zhì)教育的要求.

以“精當(dāng)指導(dǎo)”促思，是培養(yǎng)創(chuàng)新意識的不竭動力

章建躍先生提出了“三個理解”，其中的“理解學(xué)生”，就是教師需要對學(xué)生數(shù)學(xué)學(xué)習(xí)的認(rèn)知規(guī)律有深入認(rèn)識和理解，并以此展開精當(dāng)指導(dǎo)，促進(jìn)學(xué)生的深入思考和探究. 因此，在解題教學(xué)中，教師需要對學(xué)生的已有認(rèn)知水平有一個準(zhǔn)確的定位，并以此展開一般性指導(dǎo)，教會學(xué)生如何分析問題，指導(dǎo)學(xué)生解決問題的方式，并對學(xué)生“學(xué)會了做哪些”“做到什么程度”做到心中有數(shù). 這樣，當(dāng)學(xué)生深入分析卻沒有思路時，教師就可以針對性地提出以下問題：你解決過類似問題嗎？在過去解決此類問題的過程中，你是如何思考的？那道題與這道題有何相同之處？可以用類似的方法來解決這個問題嗎？在教師一步步的指導(dǎo)下，點(diǎn)燃學(xué)生的思維火花，讓學(xué)生自動搜索類似問題，有效調(diào)動學(xué)生的思維儲備，提升解決問題的眼界，培養(yǎng)創(chuàng)新意識與能力.

案例3？搖 如圖2，在四邊形ABCD中，AB=DC，且E，F(xiàn)，G，H分別為AD，BC，BD，AC的中點(diǎn).

（1）試判斷四邊形EGFH的形狀.

（2）要使四邊形EGFH為矩形，四邊形ABCD需要具備什么條件？正方形呢？

以上問題的第（1）問難度較小，學(xué)生解決起來迅速而高效，而第（2）問有些難度，大部分學(xué)生思維卡殼，無從下手.

師：那我們一起來感受四邊形EGFH的每條邊和四邊形ABCD中每條邊的關(guān)系. （學(xué)生通過自主探究，很快有了思路）

師（拾級而上）：我們有沒有解決過類似的問題？（學(xué)生陷入回憶）

生1：我記起來了，課本中有這樣一道例題——如圖3，在四邊形ABCD中，AC=BD，且E，F(xiàn)，G，H分別為AB，BC，CD，AD的中點(diǎn). 證明：四邊形EFGH為菱形.

師：很好. 那你們還記得當(dāng)時我們是用什么方法解決的嗎？

生2：三角形的中位線定理.

師：能否具體一點(diǎn)？

生3：四邊形EFGH的邊與四邊形ABCD中的對角線AC，BD相關(guān).

……

本節(jié)課，筆者通過類比的思想方法引領(lǐng)學(xué)生類比舊問題來思考新問題，使新問題向舊問題順利遷移，既幫助學(xué)生解決了新問題，又促使學(xué)生學(xué)會思考，同時使其學(xué)會用類比的方法獨(dú)自研究數(shù)學(xué)問題，培養(yǎng)他們揭示已知與未知之間區(qū)別與聯(lián)系的能力，在易于學(xué)生接受的教育形態(tài)下培養(yǎng)了他們的創(chuàng)新思維.

總之，在新的教學(xué)理念下，新課堂的運(yùn)行刻不容緩. 教師需要創(chuàng)新問題情境內(nèi)容，創(chuàng)新開放性問題設(shè)計(jì)方式，創(chuàng)新指導(dǎo)方法，進(jìn)一步探究出一條培養(yǎng)學(xué)生創(chuàng)新能力的道路，有機(jī)融合創(chuàng)新教法和創(chuàng)新教學(xué)環(huán)節(jié)，使學(xué)生問題意識與創(chuàng)新意識的培養(yǎng)落到實(shí)處.