關(guān)于復(fù)函數(shù)積分中值定理的進(jìn)一步研究

崔艷，儲(chǔ)亞偉，李雯雯，葉薇薇

（阜陽師范大學(xué)，安徽阜陽236000）

0 引言

積分中值定理是分析學(xué)的重要理論基礎(chǔ)，實(shí)分析中積分中值定理在許多定理的證明和公式的推導(dǎo)中都有重要的應(yīng)用。然而由反例［1］表明這個(gè)定理在復(fù)分析中并不成立，眾所周知，復(fù)分析中解析函數(shù)只能在局部滿足類似于實(shí)分析的中值定理形式，在整個(gè)解析區(qū)域上積分中值定理的形式與實(shí)分析的積分中值定理形式不同。

近年來，國(guó)內(nèi)外專家學(xué)者對(duì)復(fù)函數(shù)積分中值定理的條件、結(jié)論進(jìn)行了大量研究，取得了一系列研究成果［2-6］。文獻(xiàn)［2］討論了區(qū)間上連續(xù)函數(shù)的復(fù)積分的中值定理，見引理1。文獻(xiàn)［3］討論了凸區(qū)域D內(nèi)直線段上解析函數(shù)的復(fù)積分的積分中值定理，見引理2。而文獻(xiàn)［4］討論了積分路徑為光滑曲線的復(fù)變函數(shù)的積分中值定理。

本文在文獻(xiàn)［2-4］的討論的基礎(chǔ)上，研究了一種新的積分路徑為一般光滑曲線的復(fù)變函數(shù)的積分中值定理，稱之為變形的積分中值定理，并將此解析函數(shù)中值定理的結(jié)論應(yīng)用于整函數(shù)上，進(jìn)而得出有關(guān)整函數(shù)的積分中值定理。

1 引理

引理1設(shè)復(fù)數(shù)a,b(a≠b)，函數(shù)f(z)沿[a,b]連續(xù)，則存在ξ,η∈[a,b]，使∫(a,b)f(z)dz=[Ref(ξ)+iImf(η)](b-a)。

引理2設(shè)函數(shù)f(z)是凸區(qū)域D內(nèi)的解析函數(shù)，z1,z2是D內(nèi)的任意兩點(diǎn)，則在z1與z2的連線段上至少存在兩點(diǎn)ξ,η使(z1-z2)。

引理3設(shè)C:z=z(t)（a≤t≤b）為區(qū)域D內(nèi)的光滑曲線，φ(z)是區(qū)域D內(nèi)單葉函數(shù)，ω=φ(z)將C映成曲線Γ，則Γ是光滑曲線。

2 主要結(jié)論

定理1設(shè)C:z=z(t)是（凸）區(qū)域D內(nèi)光滑曲線段C:z=z(t),a≤t≤b，φ(z)是區(qū)域D內(nèi)單葉函數(shù)，且ω=φ(z)將C映成曲線Γ，如果函數(shù)f(ω)沿曲 線Γ連 續(xù)，則 一 定 存 在ξ,η∈C，使 得

證明：因?yàn)棣?z)在區(qū)域D內(nèi)單葉解析，ω=φ(z)將區(qū)域D內(nèi)光滑曲線C:z=z(t),a≤t≤b映成曲線Γ，根 據(jù) 引 理1知Γ是 光 滑 曲 線，從 而

由 于Ref(φ(z(t)))φ'(z(t))和Imf(φ(z(t)))φ'(z(t))均滿足實(shí)分析中積分中值定理的條件，所以一定存在使 得因此，有

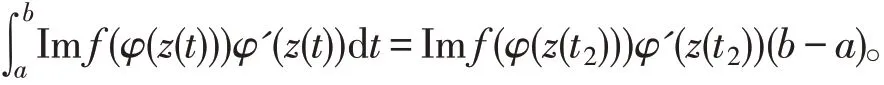
其中ξ=z(t1),η=z(t2)，證畢。

注：當(dāng)光滑曲線段C是以α為起點(diǎn)β為終點(diǎn)的直線段時(shí)，定理1即為文獻(xiàn)［4］中結(jié)果，文獻(xiàn)［4］的局限性在于積分路徑是通過單葉函數(shù)將直線段映為曲線段，本文將直線段推廣為曲線段，極大地拓展了定理的適用范圍，直接推廣了文獻(xiàn)［4］中的相應(yīng)結(jié)論。當(dāng)φ(z)=z時(shí)，定理1即為引理2，又當(dāng)φ(z)=z并且區(qū)域D為[a,b]（a,b是復(fù)數(shù)），定理1即為引理1，而文獻(xiàn)［2，3］結(jié)論為本文的兩種特殊情形。

整函數(shù)是一種重要的解析函數(shù)，將積分中值定理1應(yīng)用于整函數(shù)，從而得出關(guān)于整函數(shù)的一種積分中值定理。

3 整函數(shù)的積分中值定理

定理2設(shè)φ(z)是單葉整函數(shù)，C:z=z(t),a≤t≤b是復(fù)平面內(nèi)光滑曲線段，且ω=φ(z)將C映成曲線Γ，如果函數(shù)f(ω)沿曲線Γ連續(xù)，那么一定存在ξ,η∈C，使 得

證明：因?yàn)棣?z)為整函數(shù)，所以φ(z)在全平面內(nèi)解析，又因?yàn)镃:z=z(t),a≤t≤b是復(fù)平面內(nèi)光滑曲線段，所以存在原點(diǎn)O的某鄰域U(O;δ)，使得z(t)∈U(O;δ)，且使得φ(z)在區(qū)域D=U(O;δ)內(nèi)單葉解析，根據(jù)定理1可知結(jié)論成立。

4 應(yīng)用舉例

例如，f(z)=eiz，f(z)在整個(gè)復(fù)平面上解析，且f(0)=f(2π)，我們考慮積分，應(yīng)用定理2可分別取則成立Re[f(φ(ξ)]φ'(ξ)=

本文成功地將積分中值定理應(yīng)用范圍推廣到了積分區(qū)域?yàn)橐话愎饣€上，并將其應(yīng)用于整函數(shù)情形，這些結(jié)論既進(jìn)一步完善了整個(gè)積分學(xué)中值定理的內(nèi)容，同時(shí)所蘊(yùn)含的思想方法也將極大地推動(dòng)微積分學(xué)教學(xué)研究工作的開展。