小學數學“空間與圖形”教學中滲透轉化思想的運用
趙云華
摘要:轉化思想是小學數學“空間與圖形”教學中極為重要的一種思想和思維方法,通過滲透轉化,能夠將復雜問題簡單化,將抽象問題具體化。在小學數學“空間與圖形”教學實踐中,運用滲透轉化思想可幫助和引導學生求平面或立體圖形的面積,推導圖形面積或角度計算公式,計算立體圖形的體積,由此能夠培養和鍛煉學生的數學空間思維能力。
關鍵詞:小學數學;“空間與圖形”;教學;轉化思想;運用與滲透
數學是一門抽象的學科,其對于學生的綜合邏輯思維和學習能力有著較高的要求,在小學數學“空間與圖形”教學中,教師要善于利用“滲透轉化”思想引導學生對“空間與圖形”教學中的復雜問題進行解決和處理,幫助學生樹立終身學習意識,培養和鍛煉學生的數學空間思維能力,提升學生的數學核心素養。
一、運用“滲透轉化思想”求平面或立體圖形的面積
按照新課改要求,平面圖形和立體圖形是小學數學“空間與圖形”教學中極為重要的教學內容,其有助于激發和培養學生的空間思維,但大多數小學生缺乏空間整體思維意識和觀念,所以學生在學習這部分數學知識時,不能靈活按照新課改教學要求從上面、側面、正面觀察簡單物體的形狀,以及從不同方位觀看物體,如圓錐、圓柱、長方體、正方體等平面或立體圖形的相對位置及其展開圖。針對這一情況,教師在教學這部分內容時,要運用滲透轉化思想,指導學生將復雜的立體圖形轉化為簡單的平面數學圖形,通過對“滲透轉化”思想的深入運用,引導學生獨立分析問題和解決數學幾何圖形問題。
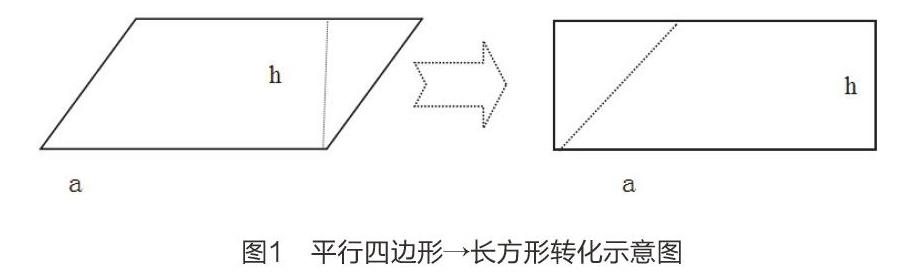
比如,在“平行四邊形”這一數學平面圖形教學實踐中,教師就可引導學生運用滲透轉化思想來分析和解決問題。例①:已知一個平行四邊形的底為a,高為h,求該平行四邊形的面積。為了讓學生能夠深入理解和掌握平行四邊形的面積計算公式,在滲透轉化過程中,教師要引導學生將這一平行四邊形滲透轉化為長方形,然后再求其面積。但由于小學生缺乏抽象思維能力,所以需要讓學生運用數學中的“割補法”將平行四邊形轉化為長方形。轉化前后圖形如下圖1所示:
如圖所示,運用滲透轉化思想將平行四邊形轉化為長方形之后,其面積就等于長方形的面積,即S=a·h,S=a·h,經簡單的轉化之后,學生能夠直觀通過圖形對比看出平面圖形之間的邏輯關聯,若直接讓學生運用平行四邊形的面積公式求解,很多學生不容易理解其面積公式,但通過圖形之間的滲透與割補轉化,就能夠將復雜問題簡單化,這種教學方法既符合小學生的認知規律,也能夠有效提高課堂教學效率。
二、運用“滲透轉化思想”推導圖形面積或角度計算公式
對于小學階段的學生而言,他們在學習“空間與圖形”相關數學知識時,除了需要認識和掌握基本的平面圖形,比如平行四邊形、梯形、三角形、正方形、長方形、圓等之外,更需要深刻理解和掌握這些平面圖形的角度、面積計算公式,但這些簡單的平面圖形面積計算公式推導相對復雜,學生不易理解和掌握,所以在課堂教學實踐中,教師不能按照傳統方法按部就班地講解,而要鼓勵和指導學生大膽學會將這些不同的平面圖形進行滲透轉化。
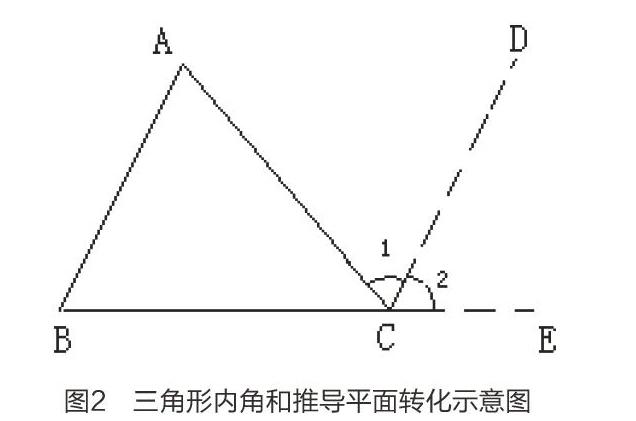
以三角形的內角和計算推導為例,在證明其內角和等于180°時,可讓學生動手剪切三角形的3個角,然后將其拼接為1條直線,最后計算這三個不同角的總和。滲透轉化平面示意圖如下圖2所示:
還比如,在求解和計算復雜的不規則平面圖形的面積時,也可應用滲透轉化思想,讓學生尋找新、舊數學知識之間的邏輯關聯,通過靈活思維,將復雜的不規則圖形轉化為常見的規則平面圖形,轉化前后圖形對比如下圖3所示:
圖3 將不規則圖形切割轉化為規則圖形
在上述案例中,無論是計算和推導三角形的內角和為180°,還是求解不規則平面圖形的面積,對于認知能力相對較弱的小學生而言,顯然是非常困難的,如果學生缺乏靈活思維意識,空間轉化或知識之間的遷移能力不強,面對這些問題學生通常總會感覺無從下手,所以,通過引導學生進行滲透轉化,可在課堂中動手實踐將裁剪后的三角形的三個角拼在一條直線中,很容易就能夠計算出三個角的總和為180°,而面對此不規則平面圖形,學生若將其轉化為規則的長方形,通過切割補全或圖形之間的遷移,也能夠順利、直觀根據長方形的面積計算出不規則圖形的面積,將抽象問題具體化。
三、運用“滲透轉化思想”計算立體圖形的體積
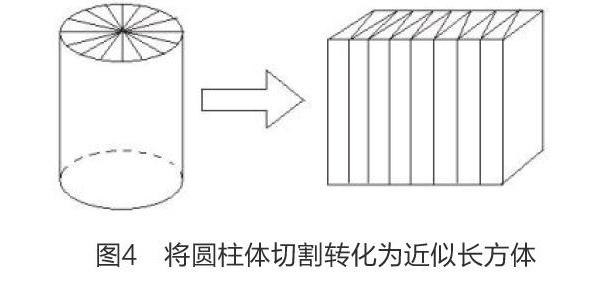
在小學數學空間與圖形教學中,教會學生快速、準確計算立體圖形的體積也是常見的教學內容。對于像正方體以及長方體這些簡單的立體幾何體,大多學生都能夠輕松求解,但面對圓柱體這些復雜的立體幾何體,學生不僅不容易理解,而且在計算其體積過程中經常容易出錯,主要原因在于學生對這些知識點理解不夠深入,對復雜立體圖形的體積計算公式掌握不夠牢固,所以在教學過程中,教師要引導學生學會自主探索,運用滲透轉化思想,將圓柱體轉化為常見的長方體,然后再根據長方體的體積計算公式求解,這種轉化和圖形遷移過程,能夠進一步加強學生對圓柱體體積計算公式的理解和認知,使數學轉化思想促進學生深入掌握相關數學原理。
例如,在計算圓的面積時,學生習慣于將圓轉化為簡單的長方形再求解其面積,同理,在計算圓柱體的體積時,教師也可引導學生運用此類滲透轉化思想,將復雜圓柱體轉化為長方體,如上圖4所示,在轉化過程中,可讓學生采用輔助的教具,以某圓柱體的上底中心為圓點,用小刀均勻切割圓柱體,將其均勻分為n等分,切割后的若干個小的不規則幾何體就能夠組成近似的長方體,長方體的長是圓周長的一半(π×r),寬是r,高不變。由于切割轉化后的長方體的底面積=長·寬,而長方體的體積=底面積·高,所以學生通過觀察轉化后的幾何體,很快就能夠找到原幾何體與轉化后幾何體之間的關聯,即可求圓柱體的體積V=S×h=(π×r×r)h。
結語
綜上,“空間與圖形”是小學數學教學中的重點和難點,教師在教學這部分數學知識時,應當結合具體的教學內容,滲透數學轉化的思想,引導和組織學生在課堂中動手實踐,把數學知識的某一形式向另一形式轉變,即化新為舊、化繁為簡、化曲為直等等。滲透轉化思想的教學可以讓學生體驗知識的形成過程,培養學生獨立分析和解決數學問題的空間思維意識,提高學生的數形結合、圖形滲透轉化能力。
參考文獻
[1]顏春燕.小學數學空間與圖形教學中轉化思想的應用[J].數學學習與研究,2017(20):107.
[2]劉長福.在小學數學“空間與圖形”教學中滲透轉化思想[J].科學咨詢(教育科研),2014(02):77-78.
[3]郭飛,溫紅.小學數學空間與圖形教學中對轉化思想的應用[J].數學學習與研究,2014(02):82.

