妙用猜撲克推理題有效提升科學素養的研究

陳海濤

【摘要】科技進步是推動國家富強、經濟發展、人民幸福、增強民族自信的重要因素和根本動力。只有廣泛提升全民族科學素養，夯實基礎，才可能支撐起尖端科技這個塔尖。而科學素養要從小抓起，在學生的各項科學素養中，分析推理能力和創新思維能力是其中必不可少的重要組成部分，猜撲克推理題正是一類以訓練學生分析推理能力和創新思維能力為主要目的的問題，學生通過對猜撲克推理題的分析和拓展性思考，通過對表面的分析發現其背后隱藏的實質，通過發現和總結規律以至于拓展改編，學生的分析推理能力和創新思維能力可以獲得充分的鍛煉，這對于提升學生的綜合科學素養是非常有利的。

【關鍵詞】猜撲克;分析推理;創新思維;科學素養

在一次小學數學教師解題比賽中，出現了一道類似這樣題目。

有人從一手紙牌中選定一張牌，他把這張牌的花色告訴X先生，而把點數告訴了Y先生，兩位先生都知道這手紙牌是：

黑桃 J、8、4、2;

紅心A、Q、4;

方塊A、5;

草花K、Q、5、4。

X先生和Y先生都很精通邏輯，很善于推理。他們之間有對話如下：

Y先生：我不知道這張牌。

X先生：我知道你不知道這張牌。

Y先生：現在我知道這張牌了。

X先生：現在我也知道了。

請問選定的是哪張牌？

這是一道經典的分析推理題，對解答者的嚴謹分析推理、發散性思維的要求較高，是一個很好的思維鍛煉過程。《義務教育數學課程標準》指出：“要發揮數學在培養人的思維能力和創新能力方面的不可替代的作用。”在數學課程中，應當注重發展學生的分析與推理能力、創新意識和實踐能力。在科學探究中，分析推理能力也有著重要的作用，《小學科學課程標準》也對學生提出了“初步學習觀察、調查、比較、分類、分析資料、得出結論等方法，能夠利用科學方法和科學知識初步理解身邊自然現象和解決某些簡單的實際問題”的要求。可見，分析推理能力在數學與科學素養中的重要性。猜撲克推理題作為分析推理類型的問題，學生通過對猜撲克推理題的分析和拓展性思考，其分析與推理的能力、創新意識都可以獲得有效的鍛煉。

下面開始經歷學生在分析解答這道題目時的研究歷程。

對于學生來講，這是一道神奇又有趣的題目：兩人的敘述從一開始的都是“不知道”，到后來的居然“都知道了”，腦洞非常大！這樣的題目往往能夠馬上激發起學生深入鉆研的興趣，而這對于培養學生的分析推理能力、嚴謹治學、大膽猜測、小心求證、發散性思維的態度和習慣是非常有利的。

大多數第一次接觸這種題目的學生，對于這道題目是無從下手的，相當多的學生以為這是腦筋急轉彎，只有少數學生讀懂了X、Y兩人對話的第一句，并且與同學展開討論，碰撞出思維的火花。

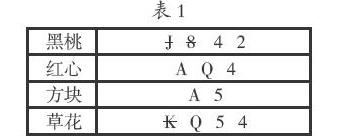
在Y先生已被告知這張牌的點數的情況下，Y先生的第一句話，卻不能確定是哪張牌。學生能夠比較容易理解這句話背后的含義：說明Y先生所知道的點數不是唯一的。這點可以通過反證法來證明：先假設Y先生知道這張牌的點數是J，他就能直接猜出是黑桃J了。同理，可以排除黑桃J、黑桃8、草花K這些唯一的點數（見表1）。

接著分析兩人對話的第二句，X先生說：“我知道你不知道這張牌。”這句話聽起來非常別扭，理解起來也特別困難。學生通過激烈的討論，才分析出“我知道你不知道”的意思是“根據我了解到的信息進行分析推理，作出的對你的判斷是，你無法確定這是哪張牌”。

在作出判斷前，還應該先找到兩個潛在的前提條件：一是X先生知道Y先生“很精通邏輯，很善于推理”，Y先生作出的判斷必定是正確的;二是X先生是知道Y先生被告知了這張牌的點數的，否則他無法作出這樣的判斷。這兩個潛在的條件同樣是解決問題的前提，如果缺乏了這兩個前提條件，解決問題的過程是有漏洞的。

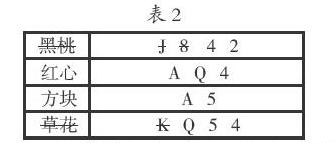
在學生想明白X先生在說出“我知道你不知道這張牌”前的潛在條件后，就能分析得到這潛臺詞的含義：“X先生所知道的花色中，每一個點數都不是唯一的，因此Y先生即使知道這個花色中任意一張牌的點數也無法作出判斷，所以我知道你一定無法確定是哪張牌。”這同樣可以通過反證法來證明：假設X先生被告知的花色是黑桃，則Y先生被告知的點數就有可能是“J”或“8”，那么Y先生是有可能猜出是哪張牌的，X先生就不能作出“我知道你一定猜不出來”的判斷了，因此推理出X先生被告知的花色一定不是黑桃;同理，由于草花K的點數是唯一的，X先生被告知的花色也不可能是草花。所以可以排除“黑桃”和“草花”兩種花色（見表2）。

兩人對話的第三句，Y先生這時候說“現在我知道這張牌了”。Y先生為什么可以作出這個判斷？跟前面X先生的分析推理過程類似，首先得分析出兩個潛在的前提條件：一是Y先生知道X先生“很精通邏輯，很善于推理”，X先生作出的判斷必定是正確的;二是Y先生是知道X先生被告知了這張牌的花色的，通過對第二句對話的分析，獲得“排除了黑桃和草花兩種花色的結論”，否則Y先生無法作出正確的判斷。

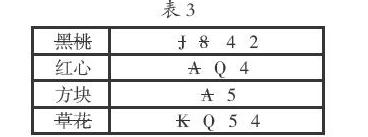
在剩下的“紅心”和“方塊”兩種花色中，由于Y先生被告知的是點數，而他能確定是哪張牌，所以Y先生這句話的潛臺詞是“被告知的點數在剩下的紅心和方塊兩種花色中是唯一的”。假如Y先生被告知的點數是“A”，則Y先生無法確定這張牌是“紅心A”還是“方塊A”，所以可以排除這兩張牌（見表3）。

最后來分析兩人對話的第四句，X先生此時也說“現在我也知道了”，同樣是基于他聽明白了Y先生的潛臺詞，要在剩下的“紅心Q”“紅心4”“方塊5”中判斷是哪張牌。由于X先生被告知的是花色，很明顯，如果他被告知的花色是紅心，則他無法確定是“紅心Q”還是“紅心4”;但如果他被告知的花色是方塊，他就可以作出準確判斷了。因此他被告知的花色是“方塊”。最終確定，從開始的13張牌中選定的一張牌是“方塊5”。

回顧整個分析推理過程，層層推進，環環相扣，只有通過嚴謹的分析推理和發散性的思維，才可以得到正確的答案。

如果教師再追問一句：“你能改編題目嗎？”把原有的撲克牌換掉一部分、或者增減一些撲克牌，能否改編出另一道推理過程嚴謹而又合理的題目？改編題目實際上就是一個創新的過程。

學生還可能會問：可否讓被選中的牌所在花色不是最少撲克牌、甚至是最多撲克牌的？發現問題比解決問題更重要，如果學生能夠提出這個問題，那就說明學生在探索解決猜撲克問題時碰撞出來的思維火花是激烈的，創新的意愿是強烈的。

事實證明，符合要求的改編方法有很多，既可以使四種花色的撲克牌同樣多，也可以使被選中的牌所在花色的撲克牌最多，在這里就不作探討了。

通過對猜撲克推理問題的分析推理、對題目進行改編、以及提出值得深入研究的問題的過程，學生的分析推理能力、發散性思維和創新意識都可以得到充分的鍛煉，更培養了學生面對困難迎難而上的意志和品格，對于學生科學素養的發展是非常有利的。