淺談學生問題意識的培養策略

沈娟

[摘? 要] 如何培養學生問題意識，讓學生形成主動探究和自然提出問題的習慣，成為所有數學教師思考的問題. 文章結合多個案例，說明培養問題意識的路徑：創設問題情境，使學生想問;保護好奇心理，使學生敢問;適當變式訓練，使學生會問;聚焦方法指導，使學生善問.

[關鍵詞] 提出問題;問題意識;培養

伴隨著時代的不斷發展，以創新思維為核心的自主創新能力得到了充分的關注，問題意識得到了廣泛的重視. 學生提出問題的能力不是靠傳授而得到的，它是學習者經過“腦風暴”后的頓悟而形成的. 因而，培養學生的問題意識必須依靠潛移默化的熏陶，讓學生形成主動探究的習慣，進而自然提出問題. 筆者結合新一輪基礎課程改革的目標，基于學生問題意識的培養，進行了多次大膽的實踐嘗試，取得了較好的效果. 現將實踐嘗試的過程和一點思考進行整理，與同仁交流.

創設問題情境，使學生想問

不少專家從辯證唯物主義認識論、數學文化以及現代數學觀等視角對“數學情境與提出問題”進行了多元化的論述，指出了實施的原則、策略以及取得的成果. 由此可見，問題情境對學生問題意識的培養意義重大. 因此，教師需從學生的認知水平、教學內容出發，有意識、有目的地創設問題情境，動搖學生已有知識結構的平衡狀態，使其產生疑惑，使他們想問，從而使整個教學過程充滿問題、充滿互動.

案例1?一元二次方程

師：基于你們自身對一元二次方程概念的理解和定位，試著寫出一個一元二次方程.

（這是學生感興趣的數學活動，自然各個躍躍欲試，呈現多樣化展示的精彩場面）

教師選擇部分方程進行展示：①x2-5=0;②x2-2x-3=0;③■x2-4x-1=0;④x2-■x+4=0;⑤ax2+bx+c=0.

師：大家一起觀察你們所寫的方程，能否進行針對性的提問？

生1：請試著求解以上一元二次方程.

生2：不對，應先判斷以上方程是否都是一元二次方程. 比如上述方程中的“⑤ax2+bx+c=0”，當a=0，b≠0時，該方程則為一元一次方程.

生3：是否可以不解方程求出以上每個一元二次方程兩根的平方和.

生4：不對，首先需判斷其是否有實根，若有，請求出方程兩根的平方和.

……

師：你們的提問都非常精彩，那老師也提一個問題. 誰能列舉一個含有字母的一元二次方程？

生5：這個簡單，（m-1）x2+2x+3=0.

生6：不對，該方程并非一定是一元二次方程. 你看，當m=1時，方程為2x+3=0，所以，只有當m≠1時，方程（m-1）·x2+2x+3=0才是一元二次方程.

生7：我認為還不夠完善，只有當m為不等于1的常數時，（m-1）x2+2x+3=0才是一元二次方程.

……

以上案例中，教師的課堂處理簡明而直接，教師的問題情境精巧而合理，自然誘發學生的問題意識，通過交流不同的思路，使其不斷地提出問題，彰顯了學生的數學能力.

保護好奇心理，使學生敢問

學生由于受到自身知識水平和理解能力的影響，提出問題的能力是有差異的，一些學生提出的問題具有較高的層次性，而有些學生的問題不切主題，甚至會有些可笑. 對于教師來說，除了以睿智激起學生提出問題的欲望，還需保護學生的好奇心理，尊重學生提出的問題，以鼓勵的言語和激勵的眼神去開啟學生的心智，讓學生敞開心扉，敢于提問，展現自己的個性.

案例2?三角形的三邊關系

師：經過剛才的探討，你們能提出哪些問題？

生1：滿足什么條件的才是直角三角形？

師：這個問題很不錯，那你是否可以解答呢？

生1：當三角形的三邊a，b，c滿足a2+b2=c2時，這個三角形即為直角三角形.

師：那三邊長a，b，c有何要求嗎？

生1：沒有，是任意的.

師：真的嗎？那我們一起試著擺一擺，看看生1的結論是不是正確呢？

（學生興致勃勃地投入操作）

生2：生1的判斷是錯誤的，三角形的三邊并非任意的.

師：那如何判斷三條線段是不是可以組成一個三角形呢？

（學生展開了討論，并對操作所得的數據進行深入分析，有了新的認識）

生3：只有任意兩條邊的和大于第三條邊，任意兩條邊的差小于第三邊才能組成一個三角形.

上述案例中，教師創造機會讓學生去提問，但卻不解決學生針對情境所提出的問題，而是留下懸念，讓學生去思考、去探究、去討論、去質疑，讓新知真正在學生的知識體系中扎根和生長，促進學生對數學知識的深刻理解[1].

適當變式訓練，使學生會問

問題是產生學習動機的載體，問題是誘發和激起求知欲的根本. 學生感知不到問題的存在，就無法真正深入思考，這樣的學習也將是淺層的;而一旦學生有了問題意識，學習才是深刻的、有效的. “授人以魚不如授人以漁”，我們可以以適當的變式訓練，引導學生比較新舊知識間的異同點而發問，再讓學生進行發散性思維，嘗試進行適當的變式，以訓練學生的問題意識和數學思維.

案例3?讓學生嘗試提問

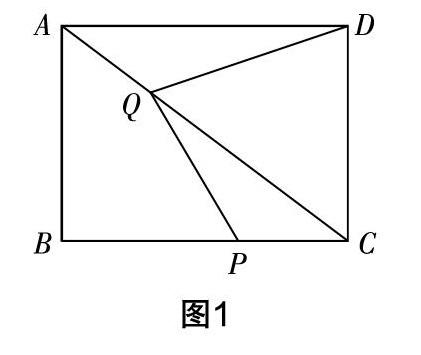
如圖1，已知矩形ABCD中，有AB=6，BC=8，且動點P從點C開始以1個單位每秒的速度，在CB上向著點B運動. 同時，動點Q以與動點P相同的速度從A點開始在AC上向著點C運動. 連接PQ，DQ，設時間為t.

生1：這是一道題目嗎？它在問什么啊？

生2：這道題目為什么沒有求解或者證明？

（教師一直微笑地看著學生，學生則一直處于困惑中）

師：愛因斯坦曾說，提出一個問題遠比解決一個問題更加重要. 而我們一直在解決問題，很少提出問題，那你們是否可以根據以上材料提出一個數學問題呢？我們可以從簡單的問題開始嘗試.

（學生思考和討論）

經過五分鐘左右的思考和探討后，學生開始提問.

生3：試求出AC的長.

生4：請試著用t來表示AQ和CP的長.

生5：當t為何值時，PQ//AB.

生6：當t為何值時，CP=PQ.

生7：試求出線段QD的最小值.

生8：當t為何值時，△CPQ為等腰三角形.

生9：當t為何值時，△ADQ為等腰三角形.

生10：當t為何值時，△CPQ為直角三角形.

生11：試求出四邊形ABPQ面積的最值.

……

以上案例中，教師問題的設計具有很大的開放性，由于已經到達初中的復習階段，所以學生提問的深度和廣度較大，涉及的圖形和知識也會很多. 學生在思考如何提問、提出什么問題和從哪個方面提問的時候，會充分調動自身已有知識經驗，從而達到本節課的學習目的. 在學生思考并提出問題的過程中，教師可以適時點撥和引導，盡量讓學生的問題既具有多樣化的特征，又具有一定的探究意義[2].

聚焦方法指導，使學生善問

馬赫穆托夫在他的“問題教學”理論里提出，問題的提出主要分為以下三個階段：第一階段：分析問題情境;第二階段：“看出”問題實質;第三階段：通過語言來概述問題. 由此可見，提出問題也是“有法可依”的. 因此，為了更好地培養問題意識，教師需聚焦方法指導，潛移默化地教給學生提出問題的方法，使學生勇于提問又善于提問，使我們的課堂交流深入而高效，使學生提出問題能力的培養落到實處.

案例4?相似三角形的判定

師：相似三角形的一種特殊情況是什么？

生1：是全等三角形.

師：很好. 那全等三角形的判定有幾種方法？

生2：有SSS，SAS，ASA和AAS這4種方法.

師：很好，那么據此你可以提出哪些問題呢？下面請分組討論.

（學生投入討論，片刻后有了結果）

生3：若兩個三角形的兩個角對應相等且一組對應邊之比相等，那么它們相似嗎？

生4：不對吧，一組對應邊之比好像并不存在與誰相等的問題.

師：那這個問題該如何修正呢？

生4：若兩個三角形的兩角對應相等，那么它們相似嗎？

師：還有其他問題嗎？

……

上述案例中，教師以類比的方法，讓學生提出問題，并將問題交給學生一起去研究. 這樣一來，既讓學生敢于提問，又可以幫助學生準確得知問題的優劣，從而及時反思問題本身，使其更加善于提問. 當在課堂上提出問題成為一種常態，學生的問題意識才是真正意義上的落地生根[3].

總之，倘若教師的提問可以促進學生的數學思考，那學生的問題意識不僅展現了自身思考的價值，還能促進師生的共同思考. 教師只有重視和培養學生提出問題的能力，才能培養學生的問題意識和創新思維能力，實現數學課程的育人價值.

參考文獻：

[1]張奠宙，張蔭南. 新概念：用問題驅動的數學教學[J]. 高等數學研究，2004（5）.

[2]李鵬，傅贏芳. 論數學課堂提問的誤區與對策[J]. 數學教育學報，2013，22（4）.

[3]溫建紅. 數學課堂有效提問的內涵及特征[J]. 數學教育學報，2011，20（6）.