小學數(shù)學數(shù)形結合思想教學實踐與探索

胡雪貞

摘?要：小學階段的學生，他們思維能力的發(fā)展還不成熟，為了幫助他們提升并拓展這一能力，教師在進行數(shù)學教學時，靈活運用數(shù)形結合的方法來提升課堂教學質量，引導學生領悟數(shù)形結合的真正思想，使他們在遇到數(shù)學問題時能夠做到活學活用，教師在教學中結合數(shù)形思想還可以增強學生的實踐能力，為他們以后更好的學以致用奠定基礎。

關鍵詞：小學數(shù)學;數(shù)形結合思想;教學實踐

縱觀目前的小學數(shù)學，數(shù)形結合思想已經(jīng)被教師普遍運用到了數(shù)學教學中，這種新型的教學模式對于加強學生的理解力和記憶力有很大幫助。教師在數(shù)學教學時，運用數(shù)形結合進行講解，學生會更直觀形象的理解數(shù)學知識并加以掌握，同時還會激發(fā)學生探索新知識的興趣，拓寬了學生知識面提升了學生的思維能力。

一.抽象概念與數(shù)形結合

數(shù)學概念比較抽象難懂，對于理解能力較差的小學生來說，理解數(shù)學概念更是難上加難。某些教師講解數(shù)學知識時，仍舊采用讓學生死記硬背的傳統(tǒng)教學方法，導致學生在遇到新的學習問題時手足無措無法活學活用。針對此現(xiàn)狀，教師需要改變傳統(tǒng)的教學模式，靈活教學，運用數(shù)形結合的新思想，把抽象的東西形象化，去繁從簡，有助于學生對概念的理解并做到學以致用。

如，新課標人教版的《分數(shù)的初步認識》中，教師進行教學時，為了加深學生對分數(shù)的了解，可以通過畫圖來講解，將圖1整個長方形看做一個整體，平均分成三等份，其中的陰影部分占了兩份，用數(shù)字表示是2/3，空白的部分占了一份，用數(shù)字表示是1/3，同樣方法，把圖2看做一個整體，分成6等份，空白的部分占了1份，用數(shù)字表示就是1/6，運用這種數(shù)形結合的方法進行教學，學生對分數(shù)有了更直觀的認識，同時對“單位1”也有了更深的印象，不僅鞏固了所學知識，也使學生在以后的數(shù)學問題中做到靈活不死板。

二.數(shù)學規(guī)律與數(shù)形結合

有許多數(shù)學題目，經(jīng)常會隱藏一些規(guī)律且不易被學生發(fā)現(xiàn)，教師在進行這方面的數(shù)學教學時，引導學生運用數(shù)形結合來分析解決問題，將難解的問題用圖形直觀表示出來，從中尋找規(guī)律，進而找出問題中隱藏的知識點，這種探索學習的過程，也會激發(fā)學生的學習樂趣。

如，小學一年級新課標人教版《找規(guī)律》教學中，為了加深學生對規(guī)律的認識，教師可以利用圖形來進行教學，舉一種常見的例型，在馬路上安裝五盞燈該怎樣安裝合適，學生剛看到這種題的時候是非常茫然的，不知道怎么辦，這種情況下，教師可以在黑板上通過畫圖的方式和學生一起尋找問題的答案-怎樣安裝才能達到要求，教師要引導學生先理清路燈之間的平均距離和路燈的總個數(shù)，假設在馬路兩端都安裝路燈該怎么做，通過圖3引導學生思考并得出答案：路燈的間隔數(shù)+1=路燈總個數(shù);假如只在馬路一端安裝該怎么解這道題，繼續(xù)通過畫圖的方法來講解，答案也很快就出來了，如下圖4：路燈數(shù)=路燈的間隔數(shù);教師引導學生想象還有沒有其他安裝方法，假設馬路兩邊都不安裝路燈又該怎么做這種題，教師和學生可以一起畫圖，答案很快就會得出，如下圖5：路燈間隔數(shù)-1=路燈數(shù)量。教師通過數(shù)形結合的方法把復雜的問題簡單化，通過畫圖的方式讓學生非常直觀的找出了問題的答案，這不僅鞏固了學生的數(shù)學知識，還使學生在遇到類似的數(shù)學問題時能做到舉一反三。

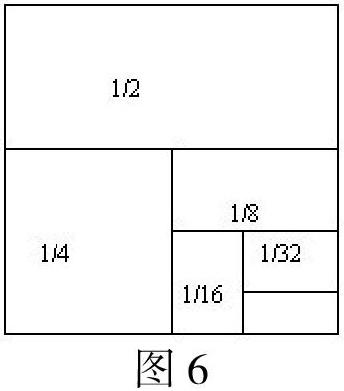
還比如，教師在講解“分數(shù)的加法”時，會遇到比較特殊的分數(shù)，通常教師都會讓學生觀察并找出規(guī)律，大部分學生在做這類數(shù)學題時，都會運用通分的方法來計算，比較費時費力，這時教師可以運用數(shù)形思想來教學，通過此種方法，學生很容易就能發(fā)現(xiàn)規(guī)律，舉例，求+的正確答案，教師先在黑板上畫圖，通過簡單直接的方式，學生很快發(fā)現(xiàn)，圖形空白處可以用1-來表示，正確答案也就隨之而出（如圖6），通過這種數(shù)學結合的解題思路，學生不僅學會了觀察思考，以后在相似的問題中，學生也能按照教師所教方法來解題，大大鍛煉了學生的思維能力。

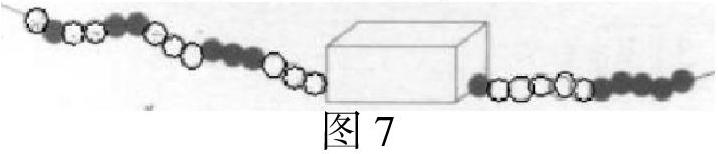
又如，把藏在盒子里面的圓珠畫出來，通過畫圖的方式（如圖7），學生很快能發(fā)現(xiàn)規(guī)律并準確的做出答案，這種去繁從簡的方法，既加深了學生對新知識的了解，也拓展了學生的學習思維。

三.復雜難題與數(shù)形結合

隨著數(shù)學科目的增加，學生積攢的數(shù)學知識也增多了，但隨之面臨的數(shù)學難題也越來越多，通常這類數(shù)學題目涉及的知識面比較廣，在解決這類問題時學生要開動大腦，拓寬思路，嘗試運用各種解題方法來尋求答案，但大部分學生做題時不知如何下手，如果通過數(shù)形結合的方法來解題，把復雜的問題簡單化，學生解題過程會變得異常輕松，學習效率也會得到大幅提升。以應用題為例，小學數(shù)學應用題不僅是學生必須掌握的重點也是知識難點，怎樣使學生更好的吸收這些知識并加以靈活運用，數(shù)形結合就很好的解決了這一問題。

如，李磊家從超市購買了一袋小米，吃了5/8之后還剩15千克，這袋小米一共有多重。在做這類題型時，教師要引導學生先分析問題里面主要數(shù)字的關系（已知數(shù)和未知數(shù)的關系），這時可以利用數(shù)形結合的方法來直觀的找答案（如圖8），然后引導學生思考：吃了5/8應該還剩3/8，這剩下的15千克和3/8是互相對應的，答案通過簡單的除法很容易就得出了，同樣的，如果李磊家買的小米重40千克，已經(jīng)吃了5/8，還剩多少呢。如圖9，教師通過反復畫圖講解，加深了學生對數(shù)形結合的認識，同時也幫助學生鞏固了以前學過的舊知識。大部分學生在做數(shù)學難題的時候，都是死搬硬套，不會靈活的找問題的切入點，這就需要教師在數(shù)學教學時，反復滲透數(shù)形思想，提升學生對數(shù)形結合的認知度以便在遇到各類數(shù)學難題時能做到活學活用，這不僅提高了教師的教學質量，也為學生在以后的學習生涯中輕松應對各種問題打下了良好的基礎。

總而言之，教師對學生進行數(shù)學講解時，充分融合數(shù)形結合思想，把問題從抽象變形象，從復雜變簡單，使學生對數(shù)學知識的理解更容易并真正掌握，不僅使學生的學習思路拓寬了，也鍛煉了學生善于思考和觀察問題的能力，激發(fā)了學生學習數(shù)學的積極性，提升了教師的課堂效率，學生通過對數(shù)形思想的進一步領悟，有助于以后深度數(shù)學的學習。

參考文獻

[1]?盧芳.小學數(shù)學教學中數(shù)形結合思想的融入與滲透方式探究[J].考試周刊，2020（80）：71-72.

[2]?孟令巧.寓數(shù)于行，以形助數(shù)——淺談數(shù)形結合思想在小學數(shù)學教學中的應用[J].小學生（中旬刊），2020（09）：83.

[3]?葉美華.小學數(shù)學教學中“數(shù)形結合”思想方法應用探究[J].讀寫算，2020（24）：150-151.