峰回路轉(zhuǎn) 天塹通途

許銀伙

(福建省泉州外國(guó)語(yǔ)中學(xué) 362000)

(2)若存在不過(guò)原點(diǎn)的直線l使M為線段AB的中點(diǎn)，求p的最大值.

(2)設(shè)點(diǎn)A(x1,y1)(x1>0,y1>0)，B(x2,y2)，M(x0,y0)，由橢圓C1和拋物線C2的對(duì)稱性得：直線l的斜率存在且不為0，設(shè)直線l方程：y=kx+m(k>0).

思考一聯(lián)立橢圓C1和拋物線C2方程，可得點(diǎn)A關(guān)于參數(shù)p的坐標(biāo).聯(lián)立直線l與橢圓C1方程，運(yùn)用韋達(dá)定理可得點(diǎn)M(x0,y0)坐標(biāo).聯(lián)立直線l與拋物線C2方程，運(yùn)用韋達(dá)定理可得點(diǎn)A坐標(biāo)，由點(diǎn)A是直線l橢圓C1和拋物線C2的公共點(diǎn)，得到p關(guān)于某個(gè)已知范圍的未知數(shù)的關(guān)系式.

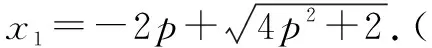
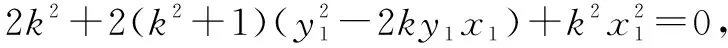
經(jīng)過(guò)上面的分析和解答，可以體會(huì)到：入手思維層次的高低，極大影響解答的運(yùn)算量.方法一屬于淺層次分析，邊摸索邊解答，走了彎路；方法二是經(jīng)過(guò)數(shù)理分析，借助參數(shù)方程的知識(shí)，摸索出了利用比例值減少參數(shù)量；方法三和四是利用方法二的結(jié)果進(jìn)一步提升優(yōu)化；方法五是在入手時(shí)提高思維的深度，簡(jiǎn)化解答難度.從方法二三四中，總結(jié)出普遍性的規(guī)律：凡是可化為關(guān)于某兩個(gè)量的齊次方程，都可以考慮比值換元解決.本題還可以設(shè)直線l方程為x=my+t(m>0)，此時(shí)相應(yīng)的方法五就是參考文[1]高考參考解答的思路.

解題能力的提升，需要磨煉，需要對(duì)問(wèn)題充分的研究與探索，即使失敗，即使走彎路.彎路可能成為風(fēng)景，如上面利用比例值減元，失敗和彎路都是進(jìn)步的基石.正所謂：千淘萬(wàn)漉雖辛苦，吹盡狂沙始到金；美人首飾侯王印，都是沙中浪底來(lái).