經(jīng)歷估測 建立猜想 轉(zhuǎn)化驗(yàn)證 提升素養(yǎng)
——關(guān)于“圓的面積”的教材對(duì)比與教學(xué)嘗試
翟運(yùn)勝(特級(jí)教師)
一、“圓的面積”教材版本對(duì)比
圓是學(xué)生在小學(xué)階段學(xué)的最后一個(gè)平面圖形,也是在小學(xué)階段唯一要學(xué)習(xí)的曲線圖形。圓在第一、二學(xué)段的數(shù)學(xué)教學(xué)中占據(jù)著重要地位,具有較高的教育價(jià)值。由于圓是曲線圖形,探索它的面積公式比直線圖形要稍難一些。在探索圓的面積公式的過程中可以使學(xué)生進(jìn)一步體會(huì)“轉(zhuǎn)化”的思想方法,滲透極限思想,增強(qiáng)空間觀念,發(fā)展數(shù)學(xué)思維,提升核心素養(yǎng)。各種版本的數(shù)學(xué)教材在編排“圓的面積推導(dǎo)”這部分內(nèi)容時(shí),都力圖充分體現(xiàn)這一知識(shí)點(diǎn)的教育教學(xué)價(jià)值,讓學(xué)生在經(jīng)歷中成長。縱觀人教版、蘇教版、北師大版、浙教版小學(xué)數(shù)學(xué)教材中關(guān)于“圓的面積”的編排,大致可以分成兩類:一類是直奔主題,直截了當(dāng),如北師大版、人教版;另一類是估計(jì)猜測,推導(dǎo)公式,如蘇教版、浙教版。
1.編排類型一:直奔主題,直截了當(dāng)。
北師大版(圖1)在編排“圓的面積”時(shí),直接提問:如何得到一個(gè)圓的面積呢?學(xué)生以往的經(jīng)驗(yàn)是數(shù)格子,但是由于圓是一個(gè)曲線圖形,會(huì)出現(xiàn)不滿整格的現(xiàn)象,這種方法僅能求出一個(gè)圓的大約面積,不能迅速準(zhǔn)確地求出圓的面積,顯然是不方便使用的。基于已有的數(shù)學(xué)活動(dòng)經(jīng)驗(yàn),學(xué)生順理成章地想到能否把圓轉(zhuǎn)化成以前學(xué)過的圖形,在這個(gè)過程中,強(qiáng)化了學(xué)生轉(zhuǎn)化的意識(shí),提升了遷移類推的能力。這樣的編排相對(duì)直接,教師課堂教學(xué)實(shí)施相對(duì)比較容易,對(duì)學(xué)生可能想到的探究路徑進(jìn)行充分地預(yù)設(shè)與應(yīng)對(duì),符合學(xué)生的認(rèn)知規(guī)律,容易引發(fā)學(xué)生的探究興趣。

圖1
人教版教材在編排“圓的面積”教學(xué)時(shí),與北師大版教材類似,創(chuàng)設(shè)了這樣一個(gè)問題情境:每平方米草皮8 元,這個(gè)圓形草坪的占地面積是多少平方米?引導(dǎo)學(xué)生提問:怎樣計(jì)算一個(gè)圓的面積,引發(fā)學(xué)生探求圓面積的內(nèi)在需要。在教學(xué)中,教師引導(dǎo)學(xué)生想一想能否把圓轉(zhuǎn)化成以前學(xué)過的圖形,從而推導(dǎo)出圓面積的計(jì)算公式。這樣的編排在常態(tài)化的實(shí)施過程中,有的教師會(huì)直接演示把圓沿著直徑切開,拼擺成近似的長方形推導(dǎo)出公式,教學(xué)過程中學(xué)生有可能會(huì)成為“操作工”。教學(xué)中,教師應(yīng)當(dāng)給學(xué)生嘗試、遇阻、折回,找最佳切割方式的機(jī)會(huì),組織引導(dǎo)學(xué)生經(jīng)歷思維曲折的探索過程。
2.編排類型二:估計(jì)猜測,推導(dǎo)公式。
蘇教版教材在編排“圓的面積”(圖2)教學(xué)時(shí),設(shè)置了兩個(gè)例題,例7 是引導(dǎo)學(xué)生體會(huì)圓的面積與半徑的平方之間的關(guān)系。在此之前,學(xué)生沒有探究圓面積計(jì)算的需求,需要教師另外設(shè)計(jì)課堂教學(xué),考慮到常態(tài)課的教學(xué)狀況,如果能把創(chuàng)設(shè)面積計(jì)算的情境隱含在其中,對(duì)一線教師能有所暗示就更好了。在例7 中,以正方形的邊長為半徑畫出大小不同的圓,讓學(xué)生借助正方形來估計(jì)圓的面積,通過數(shù)格子計(jì)算圓的面積大約是正方形的幾倍,也就是半徑的平方的幾倍。從而發(fā)現(xiàn)圓的面積與半徑的平方之間的關(guān)系。例8 則是把圓等分成若干份,然后拼成長方形來推導(dǎo)出圓的面積公式。在這個(gè)過程中發(fā)展學(xué)生有序思考和簡單推理的能力。在實(shí)際教學(xué)時(shí),這兩個(gè)例題放在一節(jié)課中,在家常課的狀態(tài)下,一節(jié)課的教學(xué)時(shí)間是挺緊張的。從例7 的教學(xué)來看,教師引導(dǎo)組織的痕跡比較重,學(xué)生多是在教師的指令與點(diǎn)撥下操作與思考。因?yàn)橐话闱闆r下,學(xué)生很難想到以正方形的邊長為半徑畫出大小不同的圓,以此探索圓的面積除以它的半徑的平方是否存在規(guī)律。人類對(duì)于圓面積的研究經(jīng)歷了千百年的時(shí)間,想在一節(jié)課中幫助學(xué)生經(jīng)歷這一過程,自然需要教師精心地預(yù)設(shè)、點(diǎn)撥和講授。沒有教師點(diǎn)撥引導(dǎo),學(xué)生很難想到借助正方形來嘗試求圓的面積,體會(huì)圓的面積可能是這樣的正方形面積的幾倍,也就是半徑的平方的幾倍,然后再通過例8 的公式推導(dǎo)進(jìn)行驗(yàn)證。

圖2
浙教版教材在編排“圓的面積”(圖3)這部分內(nèi)容時(shí),同樣也采用了類似估計(jì)與猜測的編排,引導(dǎo)學(xué)生思辨:圓的面積與小正方形的面積(圓的半徑的平方)有什么關(guān)系,利用圖形中的不同顏色來幫助學(xué)生思考。由于有顏色區(qū)分的暗示,多數(shù)學(xué)生能夠理解圓的面積大于它半徑的平方的2 倍,小于半徑的平方的4 倍。不過浙教版沒有安排數(shù)格子來具體計(jì)算圓的面積與小正方形面積之間的倍數(shù)關(guān)系。教學(xué)實(shí)踐證明,學(xué)生在數(shù)格子計(jì)算圓的面積時(shí),很難把格子數(shù)清楚。在計(jì)算公式推導(dǎo)的過程中,不僅組織學(xué)生把等分后剪開的圓形拼成長方形,還引導(dǎo)學(xué)生把等分后剪開的圓形拼成梯形、三角形或者是把圓形等分成32 份后不剪開,把其中的一份看作是一個(gè)小三角形,從而推導(dǎo)出圓的面積計(jì)算公式。這個(gè)編排以數(shù)學(xué)知識(shí)內(nèi)在的魅力吸引學(xué)生,提升學(xué)生的數(shù)學(xué)核心素養(yǎng),引發(fā)學(xué)生的數(shù)學(xué)研究興趣。此處對(duì)學(xué)生的操作要求與思維能力,以及教師的課堂駕馭能力提出了較高的要求,學(xué)力水平較低的班級(jí)不適合采用這種教學(xué)方式。
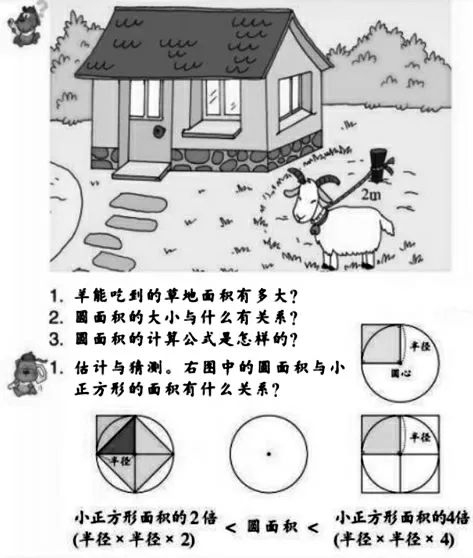
圖3
二、思考:估計(jì)猜測的環(huán)節(jié)是否必要呢?
北師大版與人教版在編排中直截了當(dāng)引導(dǎo)學(xué)生把圓的面積轉(zhuǎn)化成已學(xué)圖形,從而推導(dǎo)出圓面積的計(jì)算,此內(nèi)容較利于家常課的教學(xué)開展,而估測環(huán)節(jié)似乎不是必需的。蘇教版與浙教版在編排圓的周長計(jì)算時(shí),借助一個(gè)圓的外切正方形和一個(gè)內(nèi)接的正六邊形,確定了圓的周長與直徑之間關(guān)系的范圍,從而使猜測有據(jù)可依,并通過這一過程培養(yǎng)學(xué)生的推理能力。遵循這一設(shè)計(jì)思路,在編排圓的面積探索學(xué)習(xí)時(shí),也加入了這樣一個(gè)估計(jì)猜測的環(huán)節(jié),從提升學(xué)生數(shù)學(xué)核心素養(yǎng)的角度來看顯然是必要的,并且滲透了探究方法的習(xí)得。不同地域?qū)W生的學(xué)習(xí)背景差異較大,無論采用哪一種編排,在實(shí)施教學(xué)中都應(yīng)當(dāng)結(jié)合學(xué)生實(shí)際情況而定,不可概而論之。不過,即便加入這個(gè)猜測過程,也應(yīng)當(dāng)重新設(shè)計(jì),讓學(xué)生在真實(shí)經(jīng)歷曲折探索的過程中提升數(shù)學(xué)核心素養(yǎng)。
三、教學(xué)嘗試
1.創(chuàng)設(shè)情境,引起探究欲望。
師:(出示一個(gè)自動(dòng)旋轉(zhuǎn)噴水器動(dòng)畫)它旋轉(zhuǎn)一周所噴灌的地方是一個(gè)什么樣的圖形呢?
生:圓形。
師:關(guān)于圓我們已經(jīng)知道些什么?
(學(xué)生依次說出圓心、半徑、直徑、周長等相關(guān)的知識(shí)點(diǎn))
師:根據(jù)這個(gè)情境,你會(huì)提出什么樣的問題呢?
生:自動(dòng)旋轉(zhuǎn)噴水器旋轉(zhuǎn)一周所噴灌的土地面積是多少?
2.建立猜想,引發(fā)驗(yàn)證需要。
師:這其實(shí)就是求圓的面積,通過對(duì)圓的周長的探索學(xué)習(xí),我們得出了這樣一個(gè)結(jié)論:圓的周長是它直徑的π 倍,也就是三倍多一些。對(duì)于圓的面積,你會(huì)有怎樣的猜想呢?
生:圓的面積是不是與直徑之間有固定不變的倍數(shù)呢?
生:圓的面積與半徑之間是不是有固定不變的倍數(shù)呢?
師:(出示半徑為3cm、4cm、5cm 的圓)我們?cè)鯓又肋@些圓的面積,有什么方法嗎?
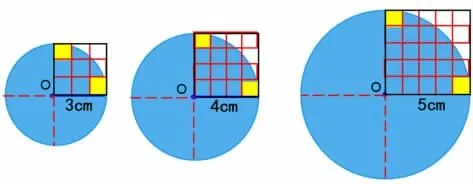
圖4
生:我們可以采用數(shù)方格的辦法來求出圓的面積。
師:為了方便數(shù)方格與計(jì)算,我們借助了與圓有一定關(guān)系的正方形,先數(shù)出四分之一圓的面積,再計(jì)算出整個(gè)圓的面積。
師:由于圓是曲線圖形,像圖中對(duì)角線兩端的兩個(gè)方格,非常接近滿格的算作滿格,其余不滿一格的按半格計(jì)算。
(學(xué)生填一填,然后依次匯報(bào),完成下表)

?
師:你有什么發(fā)現(xiàn)呢?
生:我們發(fā)現(xiàn)用圓的面積除以半徑以后,商并不是一個(gè)固定不變的數(shù)。
師:用圓的面積去除以相應(yīng)圓的直徑呢?
(學(xué)生用計(jì)算器計(jì)算發(fā)現(xiàn),圓的面積與直徑之間也沒有固定的倍數(shù)關(guān)系)
師:看來圓的面積與半徑和直徑都沒有明確的倍數(shù)關(guān)系,那么它與什么有關(guān)系呢?請(qǐng)看下圖。
(課件依次出示)

圖5
師:從這幅圖中,你能得出圓的面積與小正方形之間有怎樣的關(guān)系呢?先獨(dú)立思考,再小組討論。
生:圓的面積一定小于正方形面積的4 倍。
生:圓的面積一定大于正方形面積的2 倍。
師:圓的面積大于正方形面積的2 倍,而小于正方形面積的4 倍。
師:小正方形的邊長是圓的半徑,這句話還可以怎樣說呢?
生:圓的面積大于它半徑的平方的2 倍,而小于它半徑平方的4 倍。
師:根據(jù)這幅圖,你又會(huì)提出怎樣的猜想呢?
生:圓的面積會(huì)不會(huì)與半徑的平方之間有固定不變的倍數(shù)關(guān)系呢?
(教師出示下面的表格,學(xué)生填寫)
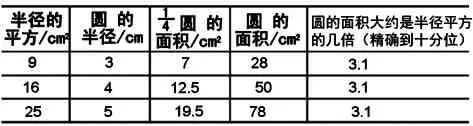
?
師:觀察表格,你有什么發(fā)現(xiàn)呢?
生:我發(fā)現(xiàn)圓的面積大約是它半徑的平方的3.1倍。
生:圓的面積大約是半徑的平方的3 倍多一些。
師:據(jù)此,你又會(huì)提出怎樣的猜想呢?
生:都是三倍多一點(diǎn),這個(gè)數(shù)會(huì)不會(huì)就是圓周率呢?圓的面積會(huì)不會(huì)就是圓半徑的平方的π 倍呢?
師:大家真了不起!下面我們就來驗(yàn)證這一猜想。
3.轉(zhuǎn)化推導(dǎo),經(jīng)歷驗(yàn)證過程。
師:同學(xué)們回憶一下,以前我們是用什么方法來推導(dǎo)平面圖形的面積計(jì)算公式呢?
生:通過剪、拼、旋轉(zhuǎn)等方法把新圖形轉(zhuǎn)化成已經(jīng)學(xué)過的圖形。
師:圓的面積計(jì)算公式是不是也能這樣獲得呢?
生:我們可以嘗試一下,把圓轉(zhuǎn)化成已經(jīng)學(xué)過的圖形。
師:好!要注意從哪兒下手剪拼最有可能轉(zhuǎn)化成所學(xué)過的平面圖形。
生:既然圓的面積和它的半徑有關(guān),我們想沿著圓的半徑剪開。
師:究竟可不可以,我們來試試看。先把圓4 等分,誰來擺一擺?
學(xué)生操作如下(圖6):

圖6
師:你還想把圓等分成多少份呢?(8 份)我們把這個(gè)圓平均分成8 份,再觀察這個(gè)圖形,你有什么發(fā)現(xiàn)呢?
學(xué)生操作如下(圖7):
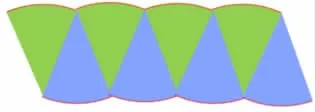
圖7
師:你們也想自己動(dòng)手拼一拼嗎?老師在你們的材料袋里放了將圓16 等分的紙片,拿出來拼一拼,貼在《研學(xué)單》上。
師:從展示的幾組由圓轉(zhuǎn)化而來的圖形中你發(fā)現(xiàn)了什么?
生:隨著份數(shù)的增加,平行四邊形的底這條曲線看起來就越來越直了。
師:想象一下,照這樣再平均分下去會(huì)怎樣呢?
生:拼成的圖形會(huì)變成一個(gè)長方形。
教師課件演示把圓等分成(64 份、128 份、256份……),學(xué)生由衷地發(fā)出贊嘆聲(圖8)。

圖8
師:你有什么發(fā)現(xiàn)呢?誰來代表你們小組匯報(bào)一下?
生:長方形的長是圓周長的一半,用字母表示就是πr,長方形的寬相當(dāng)于平行四邊形的高,是圓的半徑r。圓的面積公式就是:S=πr×r=πr2。
師:通過這個(gè)推導(dǎo)過程,驗(yàn)證了我們的猜想,那就是——
生:圓的面積果然是它半徑的平方的π 倍!
師:“果然”一詞用得真好。到目前為止,我們發(fā)現(xiàn)了圓蘊(yùn)含著一個(gè)規(guī)律,圓的周長是它半徑的2π倍,圓的面積是它半徑的平方的π 倍。回想一下,我們是怎樣探索圓面積的呢?
生:我們是從圓的周長是它直徑的π 倍,推想圓的面積會(huì)不會(huì)也是直徑或是半徑的固定的倍數(shù)。
師:然后呢?
生:我們發(fā)現(xiàn)圓的面積除以直徑或是半徑不是一個(gè)固定不變的數(shù),借助一個(gè)邊長是半徑的小正方形,我們發(fā)現(xiàn)圓的面積小于圓半徑的平方的4 倍,而大于圓的半徑的2 倍。
生:通過數(shù)格子計(jì)算得出圓的面積是它半徑的平方的3.1 倍,我們就猜想圓的面積會(huì)不會(huì)是它半徑的平方的π 倍。
師:再然后呢?
生:我們把圓轉(zhuǎn)化成長方形,推導(dǎo)出圓的面積,從而驗(yàn)證了圓的面積果然是它半徑的平方的π 倍。
師:我們?cè)谄渲羞\(yùn)用了推想、猜測、轉(zhuǎn)化等探究數(shù)學(xué)問題的方法。
師:其實(shí),16 世紀(jì)德國數(shù)學(xué)家開普勒就對(duì)圓的面積進(jìn)行過深入的探究。
(課件視頻介紹,圖9)

圖9
四、教后思考
在上面的教學(xué)過程中,教師首先組織學(xué)生猜測:圓的面積可能與什么有關(guān)系?學(xué)生一般會(huì)猜測圓的面積與半徑或是直徑有關(guān)系,這是不容忽視的事實(shí)。教師點(diǎn)撥:圓的周長除以它的半徑或者直徑的商是一個(gè)固定不變的數(shù),那么,對(duì)于圓的面積你會(huì)有怎樣的猜想呢?學(xué)生通過圓的周長計(jì)算的類比推理,自然而然地提出第一個(gè)猜想:圓的面積除以它的半徑或者直徑,是一個(gè)固定不變的數(shù)。學(xué)生再通過數(shù)格子的方式得出圓的面積,用圓的面積除以它的半徑與直徑?jīng)]有得出一個(gè)固定的數(shù)。此時(shí)研究似乎走進(jìn)了一個(gè)“死胡同”,教師的引導(dǎo)作用就充分體現(xiàn)了出來,組織學(xué)生觀察圓的面積與那個(gè)小正方形之間的關(guān)系,學(xué)生很容易發(fā)現(xiàn)圓的面積與它半徑的平方之間的倍數(shù)關(guān)系范圍,提出了第二個(gè)猜想:圓的面積與它半徑的平方之間的倍數(shù)會(huì)不會(huì)是一個(gè)固定不變的數(shù)呢?學(xué)生再用圓的面積除以它半徑的平方,發(fā)現(xiàn)了商都是三倍多一點(diǎn)。提問:據(jù)此,你又會(huì)有怎樣的猜想呢?學(xué)生提出了第三個(gè)猜想:圓的面積除以它半徑的平方的商,會(huì)是一個(gè)固定不變的數(shù)嗎?這個(gè)倍數(shù)是三倍多一點(diǎn),會(huì)是圓周率嗎?至此,學(xué)生三次提出猜想,在迂回中不斷接近問題的本質(zhì)。帶著猜想,學(xué)生把圓轉(zhuǎn)化成已知圖形,從而推導(dǎo)出圓的面積公式,驗(yàn)證了猜想。學(xué)生經(jīng)歷了推想、猜測、操作、轉(zhuǎn)化的過程,教師適時(shí)引導(dǎo)學(xué)生總結(jié)探索方法,授之以漁,從而促進(jìn)推理等數(shù)學(xué)核心素養(yǎng)的提升。
 小學(xué)教學(xué)設(shè)計(jì)(數(shù)學(xué))2020年12期
小學(xué)教學(xué)設(shè)計(jì)(數(shù)學(xué))2020年12期
- 小學(xué)教學(xué)設(shè)計(jì)(數(shù)學(xué))的其它文章
- 把握知識(shí)關(guān)聯(lián) 實(shí)現(xiàn)整體建構(gòu)
——《平行四邊形的面積計(jì)算》教學(xué)設(shè)計(jì)與說明 - 『學(xué)會(huì)思維』導(dǎo)向的課堂教學(xué)策略
- 怎樣圍面積最大
——《用列舉的策略解決問題》教學(xué)與反思 - 高效整合,讓復(fù)習(xí)課妙趣橫生
——《長方體、正方體單元復(fù)習(xí)》教學(xué)實(shí)踐與反思 - 德育在小學(xué)數(shù)學(xué)概念教學(xué)中的滲透
——以《百分?jǐn)?shù)的意義》教學(xué)為例 - 多元對(duì)比促完善 數(shù)據(jù)分析謀發(fā)展
——《條形統(tǒng)計(jì)圖》教學(xué)設(shè)計(jì)
