問題引導(dǎo)，層次遞進(jìn)

柏黎平

摘要：數(shù)學(xué)學(xué)習(xí)以發(fā)展學(xué)生數(shù)學(xué)學(xué)科核心素養(yǎng)為導(dǎo)向，而深度學(xué)習(xí)是實(shí)現(xiàn)發(fā)展學(xué)生核心素養(yǎng)的重要途徑。以“平方根”第一課時(shí)為例，以層層遞進(jìn)的問題引導(dǎo)，探討引發(fā)學(xué)生課堂深度學(xué)習(xí)的數(shù)學(xué)教學(xué)實(shí)踐。

關(guān)鍵詞：問題引導(dǎo);數(shù)學(xué)課堂;深度學(xué)習(xí)

近日，筆者接到了一個(gè)公開課任務(wù)，內(nèi)容是人教版七年級下冊“平方根”第一課時(shí)。本節(jié)內(nèi)容初看相當(dāng)簡單，就是平方根概念的引入與表示。“越簡單的課越不好上！”這是所有初中數(shù)學(xué)教師的教學(xué)共識。如何在教材原有的基礎(chǔ)上結(jié)合學(xué)生實(shí)際設(shè)計(jì)出一節(jié)較為理想的課，如何促進(jìn)學(xué)生的深度學(xué)習(xí)是值得思考的。根據(jù)最新的數(shù)學(xué)課程標(biāo)準(zhǔn)要求：數(shù)學(xué)教學(xué)要以發(fā)展學(xué)生數(shù)學(xué)學(xué)科的核心素養(yǎng)為導(dǎo)向，創(chuàng)設(shè)合適的教學(xué)環(huán)境，啟發(fā)學(xué)生思考，引導(dǎo)學(xué)生把握數(shù)學(xué)學(xué)習(xí)內(nèi)容的本質(zhì)。在數(shù)學(xué)課堂教學(xué)中，學(xué)生是教學(xué)活動的主人，因此，教師要放手讓學(xué)生參與數(shù)學(xué)學(xué)習(xí)的各個(gè)環(huán)節(jié)，從而使學(xué)生真正成為課堂學(xué)習(xí)的主體，最大限度地引發(fā)學(xué)生探究知識的內(nèi)驅(qū)力，引導(dǎo)學(xué)生主動在課堂中參與實(shí)現(xiàn)有深度的學(xué)習(xí)，促進(jìn)學(xué)生實(shí)踐能力和創(chuàng)新意識的發(fā)展。

結(jié)合本課內(nèi)容的數(shù)學(xué)史演進(jìn)歷程和上述要求，我最后確定了在學(xué)生原有知識的基礎(chǔ)上，通過層次遞進(jìn)的問題引導(dǎo)學(xué)生主動探索求知的課堂教學(xué)方式。下面就本課的教學(xué)過程談?wù)勛约旱囊恍┫敕ā?/p>

一、情境問題來源于生活

數(shù)學(xué)課堂，創(chuàng)設(shè)問題情境是非常重要的，情境引入設(shè)計(jì)應(yīng)該簡練而又有意義，應(yīng)該具有導(dǎo)向性。按“問題教學(xué)法”設(shè)計(jì)的要求，設(shè)計(jì)問題不僅要認(rèn)真分析學(xué)生在認(rèn)知過程中的內(nèi)在特征，從思維的規(guī)律出發(fā)，從培養(yǎng)學(xué)生具有良好的思維品質(zhì)出發(fā)，而且要深刻分析教材本身的內(nèi)在聯(lián)系，從新舊知識中找到學(xué)生興趣的激發(fā)點(diǎn)。本課的情境引入以“平方根”概念的產(chǎn)生為主要目的。教材的引入以實(shí)際問題“要剪面積為25的正方形紙片，表示該紙片的邊長”為主，但我認(rèn)為這在“非已知平方數(shù)”平方根的表示的引導(dǎo)上還有一定的欠缺。本課教學(xué)內(nèi)容很容易讓學(xué)生聯(lián)想到“1的平方根會表示，那么2的平方根是多少”的問題，這恰好是本課的重點(diǎn)和難點(diǎn)。于是，我在本課引入時(shí)設(shè)計(jì)了兩個(gè)遞進(jìn)的問題：

問題1：一個(gè)正方形的面積為1，它的邊長是多少？

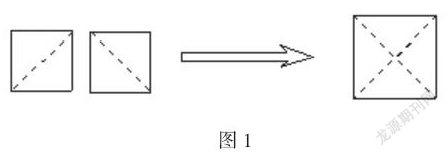
問題2：把這樣的兩個(gè)正方形經(jīng)過適當(dāng)?shù)牟眉簦隳芷闯梢粋€(gè)面積為2的正方形嗎？如果可以，那么此時(shí)該正方形的邊長是多少？

其中，第一個(gè)問題復(fù)習(xí)了新知識，并為應(yīng)用新知識做好了準(zhǔn)備;第二個(gè)問題具有一定的挑戰(zhàn)性，學(xué)生剛開始可能認(rèn)為不行，但動手操作探究之后，會發(fā)現(xiàn)是可以完成的（如圖1所示）。

由上述探究問題產(chǎn)生了本課所要探究的重點(diǎn)問題：面積為2的正方形是存在的，但它的邊長是多少呢？可以表示嗎？用數(shù)學(xué)語言表述為：“若a2=2，a=？”這就引入了新課。同時(shí)，這個(gè)問題將會成為本課學(xué)生探究的一根主線，它將串聯(lián)起全課的教學(xué)內(nèi)容。

二、引發(fā)新舊知識沖突

教學(xué)中，由于教學(xué)內(nèi)容的不同，會存在不同的內(nèi)在關(guān)系，如新舊知識之間、已知與未知之間、因果之間的關(guān)系等。在這些關(guān)系中，我們要仔細(xì)分析，從中找出主要的關(guān)系，以激發(fā)學(xué)生探究問題的興趣點(diǎn)。

在本課中，由情境引入我們可以發(fā)現(xiàn)現(xiàn)在的主要問題是：原有的舊知識已經(jīng)不夠我們解決問題了，需要新知識的介入。于是，我們就可以順理成章地給出第三個(gè)問題：

問題3：可以發(fā)現(xiàn)的確存在一個(gè)數(shù)的平方等于2，如何來描述這個(gè)存在的數(shù)？

課堂上，教師可以讓學(xué)生進(jìn)行自主表述，在此基礎(chǔ)上，再給出數(shù)學(xué)上的規(guī)范表述：“一般地，如果一個(gè)數(shù)的平方等于a，那么這個(gè)數(shù)叫作a的平方根。”同時(shí)，師生一起根據(jù)文字寫出概念的代數(shù)表示法。接著，結(jié)合情境引入中第一個(gè)問題的結(jié)論解釋平方根的意義和代數(shù)求法，并概括“關(guān)鍵是找到平方是1的數(shù)”，進(jìn)行知識的遷移。然后，學(xué)生會想到（或教師引導(dǎo)學(xué)生）用所習(xí)得的新知識“平方根及其求法”去解決情境引入中的第二個(gè)問題。學(xué)生會發(fā)現(xiàn)：問題仍然無法解決，由于2不是學(xué)過的平方數(shù)，所以找不到平方是2的數(shù)。但是，學(xué)生也有一定的收獲，他們結(jié)合剛剛學(xué)到的平方根概念，建立起了“a是2的平方根”的初步印象，知道目前要求2的平方根。

（一）深化概念內(nèi)涵

雖然沒有完全解決心中的疑惑，但不要緊，學(xué)習(xí)方面的點(diǎn)滴進(jìn)步都很寶貴，我們繼續(xù)探究。緊接著，教師引出了第四個(gè)問題。

問題4：求下列各數(shù)的平方根：

100，9，144， ? ? ? ? ?， 0，-4，-1

思考：通過研究上面幾個(gè)數(shù)的平方根，你覺得有什么要總結(jié)的嗎？

因?yàn)樗o的數(shù)是熟悉的平方數(shù)，學(xué)生能較快得出答案，并且概括出：正數(shù)有兩個(gè)平方根，它們互為相反數(shù);0的平方根只有一個(gè)，就是0;負(fù)數(shù)沒有平方根。

教師通過本題可以讓學(xué)生對平方根的概念和求法等知識進(jìn)行強(qiáng)化，同時(shí)又通過計(jì)算、觀察、概括鍛煉了學(xué)生觀察問題和概括總結(jié)的數(shù)學(xué)能力。既然又收獲了新知，教師和學(xué)生可再次回到情境引入環(huán)節(jié)中的問題2，看看這一次能否解決。此次，學(xué)生有更進(jìn)一步的收獲：正數(shù)2會有兩個(gè)平方根，即a的值有兩個(gè)，但就是無法表示出來。雖然仍舊無法解決問題，但又有所收獲，這點(diǎn)收獲也是支撐學(xué)生前進(jìn)的動力。于是，學(xué)生又繼續(xù)探究下去。

（二）固化研究成果

經(jīng)過兩次探究，學(xué)生獲得了進(jìn)步，但無法完全解決問題。此時(shí)，學(xué)生的胃口被吊得老高，應(yīng)該是欲罷不能，探究問題最終答案的積極性更高了。于是，教師趕緊推出第五個(gè)問題：

問題5：從之前的數(shù)學(xué)學(xué)習(xí)中我們知道，每一個(gè)數(shù)學(xué)概念都有專用的表示方法，那么一個(gè)非負(fù)數(shù)的平方根是如何表示的呢？

此問題由教師直接教授。第二個(gè)概念性內(nèi)容：一個(gè)正數(shù)a的正的平方根，叫作a的算術(shù)平方根，記作“ ? ? ?”，讀作“根號a”，另一個(gè)負(fù)的平方根是它的相反數(shù)，表示成“- ? ? ? ”。教師及時(shí)總結(jié)：正數(shù)a的兩個(gè)平方根記作“± ? ? ? ”，而0的平方根是0，所以記作“ ? ? =0 ”;求一個(gè)非負(fù)數(shù)的平方根的運(yùn)算叫作開平方，所以 ? ? ?中的a稱為被開方數(shù)，顯然a ≥0。此段教學(xué)內(nèi)容新知識比較多，學(xué)生可能不會完全理解，教師可以再結(jié)合上面例1中的題目加以解釋，通過舉例明確求平方根的步驟和表示方法。

（三）例題探究2，對比感受概念表示方法

由于例1的數(shù)都為平方數(shù)，缺乏本課的重點(diǎn)“非已知平方數(shù)”的平方根的求法，我們需要進(jìn)行適當(dāng)?shù)淖兪接?xùn)練以突出本課的重點(diǎn)，也就是問題2所要解決的問題。于是，教師給出第六個(gè)問題。

問題6：將下列各數(shù)開平方：

（1）49 ? ? ? ? ? ? ?（2）1.69 ? ? ? ? （3）3

學(xué)生對（1）（2）題的解決不存在困難，解決第（3）題有所困難：已知3有兩個(gè)平方根，但無法表示出來。這時(shí)，教師再給予明確的解釋：“保留根號，‘± ? ? 。”至此，真相大白，學(xué)生馬上會想到用最新的知識來回到本課引入時(shí)無法解決的問題，答案為“ ? ? ”。終于成功了，問題得以解決。接下來再進(jìn)行適當(dāng)?shù)挠?xùn)練，讓學(xué)生對本課所學(xué)新知識有一個(gè)強(qiáng)化和遷移的過程。

當(dāng)然，學(xué)生可能又產(chǎn)生一個(gè)新的問題：“ ? ? ?”到底是怎樣的一個(gè)數(shù)呢？這就讓我們留待下一節(jié)課去探究吧，我們又為下節(jié)課找到了探究問題的理由了。

以上就是筆者“問題引導(dǎo)、層次遞進(jìn)”的“平方根”第一課時(shí)的設(shè)計(jì)思路。本課以求“2的平方根”問題為一根主線，通過層層遞進(jìn)的幾個(gè)數(shù)學(xué)問題，串起本課要學(xué)習(xí)的各個(gè)知識點(diǎn)，引導(dǎo)學(xué)生逐步進(jìn)行探究，使學(xué)生的認(rèn)知從模糊到清晰，引發(fā)學(xué)生深度思考，最終得出問題解決方案。這樣的設(shè)計(jì)比較符合學(xué)生探究新知、認(rèn)識新知的規(guī)律。

參考文獻(xiàn)：

[1]王斌興.在歡樂中成長：名師講述最具活力的課堂愉快教學(xué)[M].重慶：西南師范大學(xué)出版社，2008.

（責(zé)任編輯：奚春皓）