“學”的活動：找準學習過程的有效支點

焦歡歡

【摘 要】“學”的活動，意指能幫助學生學習的有目的、有計劃組織的有關(guān)學習的活動。支點，在教學中是指實現(xiàn)真正學習、高效學習的關(guān)鍵點、中心點。有效的“學”的活動，是找準學習過程的有效支點。本文以《認識圓柱》一課為例，通過課始“制作名片”活動，找準認知起點，收集有關(guān)圓柱的前概念;課中“玩轉(zhuǎn)圓柱”，立足深度探究，建立有關(guān)圓柱的表象;課尾“創(chuàng)造圓柱”活動，促進整體建構(gòu)，建立有關(guān)圓柱的認知結(jié)構(gòu)，從而豐富學生學習圓柱的過程。

【關(guān)鍵詞】“學”的活動 支點 圓柱

“學”的活動，顧名思義，意指能幫助學生學習的有目的、有計劃組織的有關(guān)學習的活動。“學”的活動的目標指向幫助學生學習。支點，在教學中是指實現(xiàn)真正學習、高效學習的關(guān)鍵點、中心點。在一節(jié)數(shù)學課中，有效的“學”的活動，能將抽象的數(shù)學知識具體形象化，讓學生在活動中加深體驗和理解，這恰恰是實現(xiàn)真正學習、高效學習的關(guān)鍵點和突破點。筆者以《認識圓柱》一課為例，根據(jù)學生由淺入深、由局部到整體的認知規(guī)律，設(shè)計了三個“學”的活動：課始，通過“交流名片”活動，找準認知起點，收集學生有關(guān)圓柱的前概念;課中，通過“玩轉(zhuǎn)圓柱”，立足深度探究，建立有關(guān)圓柱的表象;課尾，通過“創(chuàng)造圓柱”活動，促進整體建構(gòu)，建立有關(guān)圓柱的認知結(jié)構(gòu)。通過以上“學”的活動，豐富學生學習的過程，點亮教學的黑洞，讓“學”的路徑變得清晰可見。

一、課始“制作名片”活動：找準認知起點，敞亮有關(guān)圓柱的前概念

在教學《認識圓柱》一課時，課前，教師可以通過設(shè)計“學”的活動，找準學生的認知起點。心理學家指出：“學生是帶著世界如何運轉(zhuǎn)的前概念走進課堂的。”前概念是學生在進入課堂前，對本課所學內(nèi)容已經(jīng)具有的自己樸素的認識與看法。正如本節(jié)課，在教學前，學生通過觀察和已有生活經(jīng)驗，對圓柱已經(jīng)具有自己的前概念。因此，在課始，教師設(shè)計了“制作名片”的活動，組織同伴交流思考，讓學生有關(guān)圓柱的前概念得到充分暴露，以便于找準教學的起點和方向。

【教學片段一】

教師出示要求：結(jié)合桌上的圓柱物體，請你給圓柱做個名片，并準備匯報。

學生匯報如下：

生：我覺得側(cè)面展開不一定是長方形，也可能是平行四邊形。

師：好像有點道理，你們對這個側(cè)面很感興趣，我們用手來摸摸這個側(cè)面，你有什么感覺？

生1：滑滑的，從一端摸一圈就回到頭了。

生2：有弧度，彎彎的。

生3：和平面不同。

師：摸上去彎彎的這個面，和平面不同，是一個曲面。

生：這個側(cè)面可以看成是一個平面圖形——長方形，這樣一卷，卷成圓柱側(cè)面，而且長方形的長是圓柱圓面的周長，寬是圓柱的高。

師：她通過卷，就把平面圖形變成老師說的這個曲面了。

生：老師，我還想補充，上下兩個圓面積是一樣的。

師：有什么辦法驗證？

生1：把下面畫下來，然后把上面反過來，會發(fā)現(xiàn)能重合在一起。

生2：而且側(cè)面展開可以是長方形，長方形的長就是圓面的周長，兩條長一樣，兩個圓面的周長就一樣，兩個圓面積就會一樣。

師：其實，你們說的上下兩個圓面，叫作圓柱的底面。看來，圓柱的底面是大小相等的圓。

生：我發(fā)現(xiàn)圓柱從前面看是一個長方形或是正方形。

師：拿出圓柱，我們每個人看一下，從正面看，從上面看。通過觀察，可以了解到圓柱三視圖的特征。

生1：我發(fā)現(xiàn)圓柱和長方體不一樣，它沒有棱角，也不像長方體那樣有8個頂點。

生2：我發(fā)現(xiàn)圓柱可以滾動，是因為圓柱上下勻稱。

…………

通過“制作名片”并進行交流的活動，學生有關(guān)圓柱的前概念得以彰顯和外化。學生能借助長方體、正方體的學習經(jīng)驗，有意識地想到可以把圓柱側(cè)面展開，甚至有學生在提出了圓柱側(cè)面展開圖的一些特征;還有一些學生從棱、頂點的研究視角去認識圓柱的特征，從三視圖的視角去認識圓柱。教師一個“制作名片”的活動，為學生提供了交流“學”后思考的機會，讓圓柱前概念可視化。從學生的交流情況來看，學生對圓柱并不是一無所知，甚至研究圓柱的視角遠超出教師的想象。這一活動，幫助教師找準了認知起點，了解有關(guān)圓柱的前概念。

二、課中“玩轉(zhuǎn)圓柱”活動：立足深度探究，敞亮有關(guān)圓柱的表象

課中，隨著學生認識的深入，教師要設(shè)計學的活動，提供豐富素材，立足學生進行深度探究。在幾何直觀教學中，要注重培養(yǎng)學生的空間觀念。曹培英教授指出：“小學生空間觀念的表現(xiàn)，主要就是在所學幾何形體的現(xiàn)實原型，以及幾何圖形與它們的名稱、特征之間建立起可逆的‘刺激—反應（聯(lián)想）。”因此，教師通過設(shè)計“玩轉(zhuǎn)圓柱”活動，并提供豐富的材料和探究空間，讓學生進行深度探究，使之有機會將現(xiàn)實原型和頭腦中的表象建立這樣的聯(lián)想。借助探究活動，學生可以把頭腦中內(nèi)隱的表象和思維進行外化。

【教學片段二】

師：你想怎樣玩轉(zhuǎn)圓柱？借助老師提供的材料，小組展開研究。

生1：我們是切火腿腸，我從底面切開，橫截面是兩個一樣的長方形，而且從直徑切，這兩個長方形是最大的。

生2：我們是平行底面切的，通過一片片地切，發(fā)現(xiàn)多出很多圓面，如果把這些再堆起來，圓柱就會越來越高。由此得出一個結(jié)論：圓柱是圓面向一個方向移動形成的。

師：這么一切，就發(fā)現(xiàn)了圓柱里隱藏著無數(shù)的圓面。

生1：我們是把火腿腸斜著切的，切出了橢圓形圓片。

生2：還可以切一角，發(fā)現(xiàn)是不規(guī)則圖形。

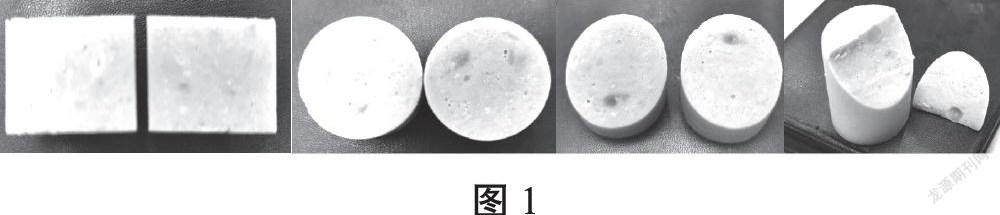
師：你們通過切，發(fā)現(xiàn)原來圓柱里面竟藏著這么多的平面圖形（見圖1）。

生1：我們小組想研究圓柱的表面積，表面積是兩個底面加上一個側(cè)面。底面好算，主要是側(cè)面不太好算，但是我們把它剪開，側(cè)面就變成長方形了，這樣就好算了。

生2：我們小組是斜著剪的，剪開以后是平行四邊形，平行四邊形的底是圓柱底面周長，兩條斜斜的邊可以重合在一起，平行四邊形的高就是圓柱的高。

生3：我們小組也是這樣剪開的，可以把多的挪過去，就成了長方形了。

生4：我們這樣剪開，這個圖形看起來很復雜，但是都可以通過轉(zhuǎn)變成長方形。

生5：然后長方形的長就是圓柱底面周長，高就是圓柱的高。

師：你們通過剪側(cè)面，可以有這么多剪法（見圖2）。

師：老師也展開了，和你們不太一樣，你們看！想象一下，如果打開，會是什么圖形呢？（見圖3）

生：平行四邊形。

師：通過展開，就把這個曲面化曲為直，變成我們熟悉的平行四邊形了。再想象一下：如果把這個圓柱很細很細地剪下去，打開會是什么？（見圖4）

生：很長很長的線。

學生通過切火腿腸、剪圓柱等“學”的活動，將頭腦中有關(guān)圓柱的特征表象外化，并研究出了圓柱平行于底面切、垂直于底面切及其他切法的特征，感受到圓柱體隱藏著無數(shù)的面，建構(gòu)出“體”和“面”的特征。又通過展開，研究了圓柱側(cè)面展開圖的特征，在不同的展開圖中，學生找到了共性：這些展開圖都可以轉(zhuǎn)化成長方形，長方形的長是圓柱底面的周長，高就是圓柱的高。教師甚至讓學生展開想象：細細地剪下去會怎樣？學生在幾何想象中，想到會是一條長長的線。教師出示材料，讓學生頭腦中內(nèi)隱的表象可視化，課中“玩轉(zhuǎn)圓柱”的活動，敞亮了有關(guān)圓柱的表象，增強了學生的空間觀念。

三、課尾“創(chuàng)造圓柱”活動：促進整體建構(gòu)，敞亮有關(guān)圓柱的認知結(jié)構(gòu)

課尾，教師要將知識進行整合，溝通知識橫向與縱向的聯(lián)系，形成認知結(jié)構(gòu)。在本節(jié)課課尾，教師通過“創(chuàng)造圓柱”這一活動，溝通了有關(guān)圓柱特征的聯(lián)系，以及圓柱與其他知識的聯(lián)系，將知識化零為整，形成板塊。學生將知識結(jié)構(gòu)內(nèi)化為頭腦中的認知結(jié)構(gòu)。在促進整體建構(gòu)的同時，豐富了學生有關(guān)圓柱的認知結(jié)構(gòu)。

【教學片段三】

師：圓柱不僅實用，而且美觀。接下來，我們就來創(chuàng)造圓柱。

生1：我用一張長方形紙，以一條邊為軸，這樣旋轉(zhuǎn)一周，就能形成圓柱。

生2：還可以繞著另外一條邊旋轉(zhuǎn)。

生3：不僅沿著邊，還可以沿著中間的線旋轉(zhuǎn)成圓柱。

師：圓柱可以這樣，通過旋轉(zhuǎn)而產(chǎn)生呢！

生1：一張圓片也是圓柱，然后好多張堆在一起，也是圓柱，堆得越多，圓柱越高。

生2：不用一堆，我就用一個圓片，用一個圓片，向上一拉，走過的路程就是圓柱。

師：圓柱還可以通過平移而產(chǎn)生！剛剛研究了圓柱的體和面、線和點，如果只給你點，會發(fā)生什么變化呢？

（教師出示點動成線、線動成面、面動成體的視頻）

師：再想，如果只給一個三角形，繞著這條軸旋轉(zhuǎn)，會形成什么圖形？

生：圓錐。

師：是的，像圓錐這樣，因旋轉(zhuǎn)而產(chǎn)生的物體叫作旋轉(zhuǎn)體;而以前學的長方體，因平移而產(chǎn)生的物體叫作柱體。再看圓柱的形成，聯(lián)系以前學的，你有什么想說的？

生：圓柱既是柱體，又是旋轉(zhuǎn)體。

師：是的，所以它既有柱體的特征，又有旋轉(zhuǎn)體的特征。現(xiàn)在你知道圓柱為什么上下一樣粗，側(cè)面是一個曲面嗎？

生1：因為是同一個圓面平移，所以上下一樣粗。

生2：一個長方形繞著一條邊旋轉(zhuǎn)，這個長方形邊的長度不變，相當于圓面不變。

生3：因為圓柱是一個長方形旋轉(zhuǎn)而成，旋轉(zhuǎn)一周，側(cè)面是曲面。

教師總結(jié)后，呈現(xiàn)以下知識結(jié)構(gòu)圖。（見圖5）

通過讓學生創(chuàng)造圓柱，學生感受圓柱可以由長方形多種方式旋轉(zhuǎn)而成，也可以由圓平移而產(chǎn)生。借助幾何體的產(chǎn)生，教師介紹了柱體和旋轉(zhuǎn)體，把圓柱和以往學習過的立體圖形建立起聯(lián)系，從而形成完整的知識結(jié)構(gòu)。圓柱的產(chǎn)生，可以解釋圓柱諸多的特征，因此，在本環(huán)節(jié)，教師最后追問：圓柱為什么上下一樣粗，側(cè)面是一個曲面？目的是讓學生形成完整的認知結(jié)構(gòu)：因為圓柱既是柱體又是旋轉(zhuǎn)體，因此既具備上下等面、一樣粗的柱體特征，又有側(cè)面是曲面的旋轉(zhuǎn)體的特征。

【參考文獻】

[1]喻平，連四清，武錫環(huán).中國數(shù)學教育心理研究30年[M].北京：科學出版社，2011.

[2]鄭毓信.數(shù)學思維與小學數(shù)學[M].南京：江蘇教育出版社，2008.

注：本文系江蘇省教育科學“十三五”規(guī)劃2020年度課題“指向課堂核心關(guān)切的支點式學習研究”（立項批準號：Xc—c/2020/08）的階段性研究成果。