兩年數學新高考試卷與課程標準的一致性研究

斯海霞 張霞

摘 ?要：以2020年和2021年高考數學全國新高考Ⅰ卷為例，基于課程標準學業質量測評框架，分析新高考試題與課程標準的一致性程度及命題特征. 研究發現，素養指向下兩年全國新高考Ⅰ卷與《普通高中數學課程標準（2017年版）》在一定程度上具有一致性，試題素養測查水平逐年趨近于課程標準中學業質量水平二的要求;但各素養皆缺失“交流與反思”方面測查，且存在素養測評不均衡、整體性不足等現象. 為有效促進教、學、評一體化銜接，發揮育人合力，建議在測評及日常教學中，加強真實情境與問題的有機融合，強化數學交流與反思，以實現素養的綜合性要求，完善數學學科核心素養生成路徑，促進學生獲得高質量學業成就.

關鍵詞：高考試卷;課程標準;核心素養;一致性

一、問題提出

高考作為重要的學業評價方式之一，是推動我國課程改革、落實素養培育的重要動力.《普通高中數學課程標準（2017年版）》（以下簡稱《標準》）明確提出將體現數學學科核心素養水平及表現的學業質量要求作為考試評價依據，以助推教、學、評的銜接. 2019年6月國務院辦公廳印發《關于新時代推進普通高中育人方式改革的指導意見》，指出高考命題要以普通高中課程標準和高校人才選拔要求為依據，實施普通高中新課程的省份不再制定考試大綱. 同年11月，教育部考試中心制定出版《中國高考評價體系》，對高考目的、內容、要求做了頂層設計，其考核內容、要求與《標準》學業質量測評要求一致，皆體現對學生學科核心素養的測評.

教育部考試中心以高考評價體系與國家課程標準為基礎構建新高考命題框架，分別于2020年和2021年命制了面向高考綜合改革省份的數學新高考試卷. 已有研究者基于高考評價體系或設計數學學科核心素養測評框架分析2020年數學新高考試題的特征，揭示全國新高考Ⅰ卷在考查《標準》與《普通高中數學課程標準（實驗）》的教學內容范圍公共部分的同時，聚焦數學學科核心素養測評，對推進新高考綜合改革，引導中學數學教學起到了積極的作用. 但并未分析新高考試卷是否符合《標準》學業質量標準素養測評要求，而高考能否真正成為促進教、學、評有機統一的學業評價有效載體，集中體現于高考試題與課程標準的一致性程度. 因此，研究以2020年和2021年全國新高考Ⅰ卷為例，以《標準》學業質量水平為測評框架，以用于課程一致性分析的SEC模式為工具，量化分析近兩年新高考試題與《標準》之間的一致性程度，揭示其命題共性與趨勢，以期為落實基于課程標準的學業評價和高中數學課堂教學提供研究證據.

二、研究設計

1. 研究對象

根據《新高考過渡時期數學學科考試范圍說明》，教育部考試中心于2020年和2021年皆命制了數學新高考試卷供高考綜合改革試點省份選用，兩份試卷考查內容及試題結構差別較少，且已有研究表明全國新高考Ⅰ卷尤其觀照了對數學學科核心素養的測查. 因此，選用近兩年的數學全國新高考Ⅰ卷作為研究對象.

2. 測評框架及研究工具

《標準》明確基于數學學科核心素養的考試命題需統籌考慮素養的四個方面、內容主線及素養水平. 將2020年和2021年全國新高考Ⅰ卷各試題考查知識點對應于《標準》課程內容標題作為研究內容的主題分類標準. 以《標準》學業質量標準中六大數學學科核心素養的“四方面三水平”作為一致性測評框架及編碼標準，對試題及課程標準進行編碼，并進行標準化處理，以此建立起指向數學學科核心素養四個方面的“核心素養 × 素養水平”的兩兩二維矩陣. 隨后根據如下公式計算Porter一致性系數[P P∈0，1]，[P]值表示兩個矩陣對應的單元格數據的符合程度，[P]值越接近1表示一致性程度越高. Porter一致性系數的計算公式為[P=1-k=1Kj=1Jakj-bkj2]. 其中，[K，J]分別表示二維矩陣的行數和列數;[akj]為一個矩陣中的第[k]行第[j]列單元格所對應的數量比率值;[bkj]為另一個矩陣中第[k]行第[j]列單元格所對應的數量比率值. 為了得到評價一致性系數的客觀標準，研究借鑒美國學者Gavin的分析方法，用二維矩陣數據仿真模擬20 000個Porter系數[P]值樣本作出分布圖象，并獲得一致性系數的分布，從而得到0.05水平下一致性系數的單側臨界值（該臨界值為置信區間左側臨界值，右側皆為1）. 通過比較臨界值與一致性系數的大小，判斷一致性系數在統計學上的意義. 當一致性系數大于或等于臨界值時，說明兩者的一致性顯著;當一致性系數小于臨界值時，說明兩者的一致性不顯著.

3. 編碼及數據分析過程

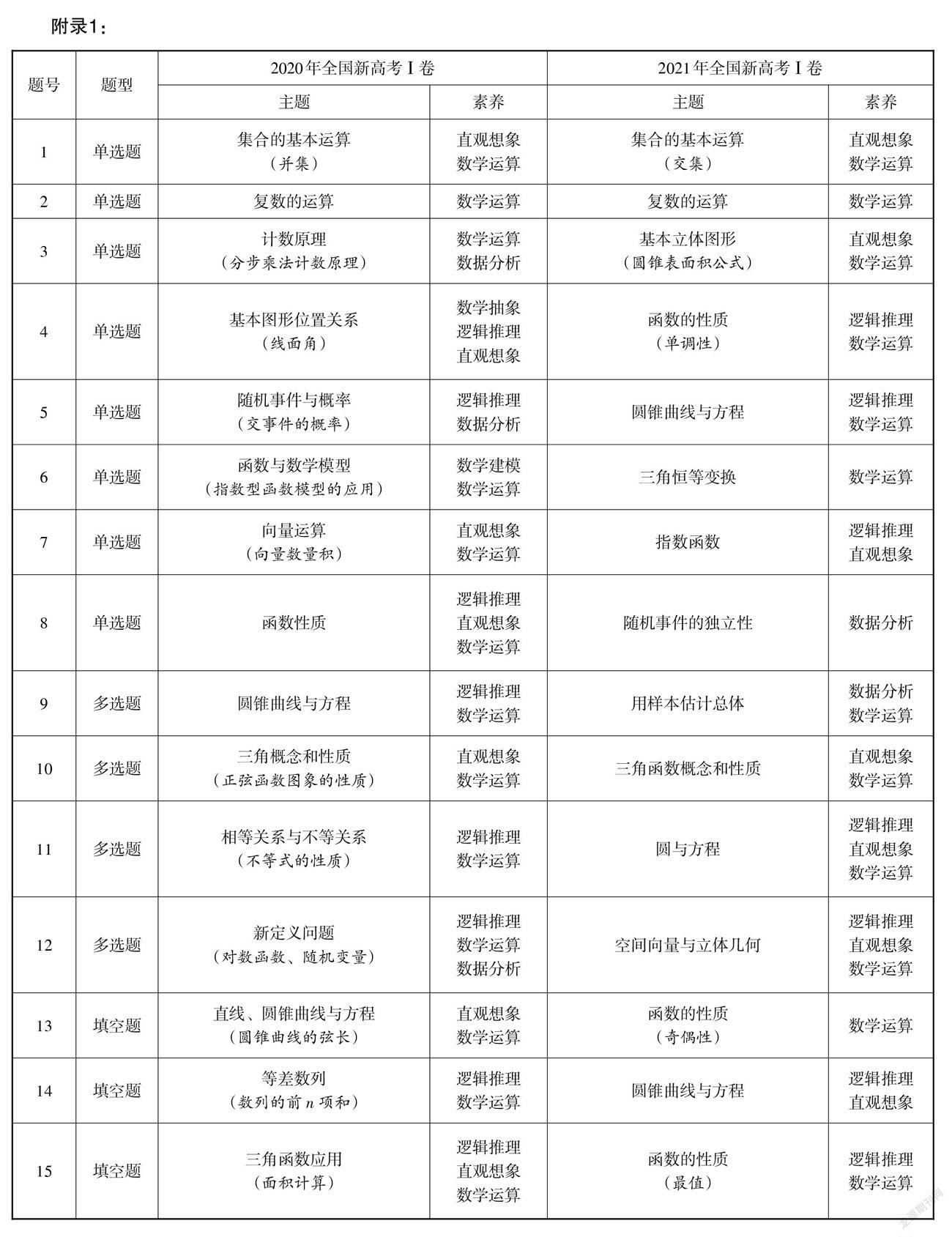
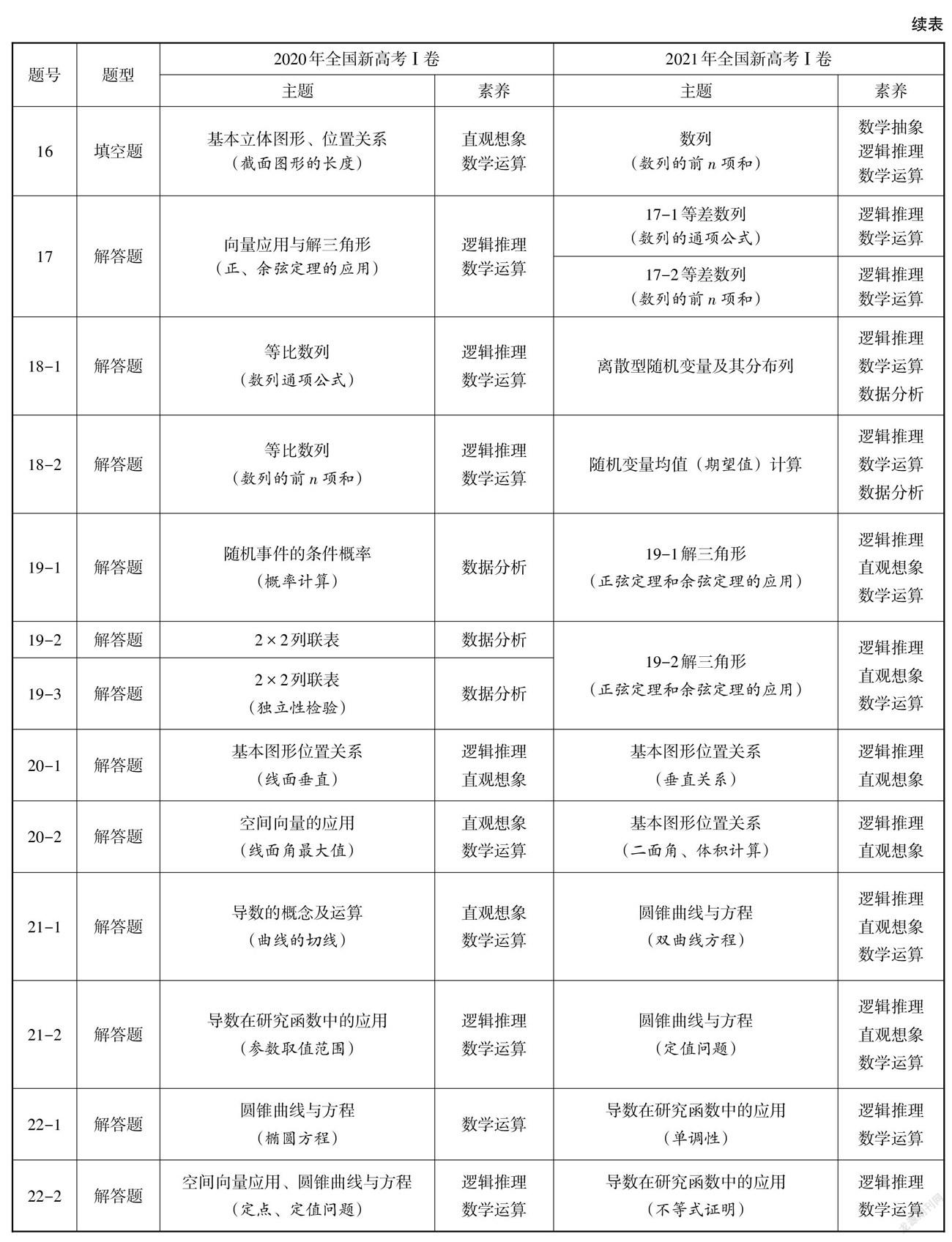
第一步：分析2020年和2021年全國新高考Ⅰ卷試題中所包含的知識點，若解答題中出現若干個小題，則以小題為編碼單位，判斷每道試題所考查的知識主題及所蘊含的數學學科核心素養;隨后根據試題的知識主題確定《標準》中所對應的主題的內容要求和學業要求，進一步分析對該知識主題的素養要求. 具體結果見附錄1.

第二步：根據數學學科核心素養“四方面三水平”測評框架對新高考試題和《標準》的內容進行編碼，確定每個知識主題所蘊含的學科核心素養各方面水平. 例如，A-S1表示該內容測查數學抽象素養的情境與問題方面第一水平. 每一個編碼對象若符合素養某方面某水平特征，則計數為“1”，且只在符合條件的最高水平層次計數. 為保證編碼的有效性，研究對象的編碼皆有三位數學學科教學專業研究生分別編碼，并通過三角論證明確編碼結果.

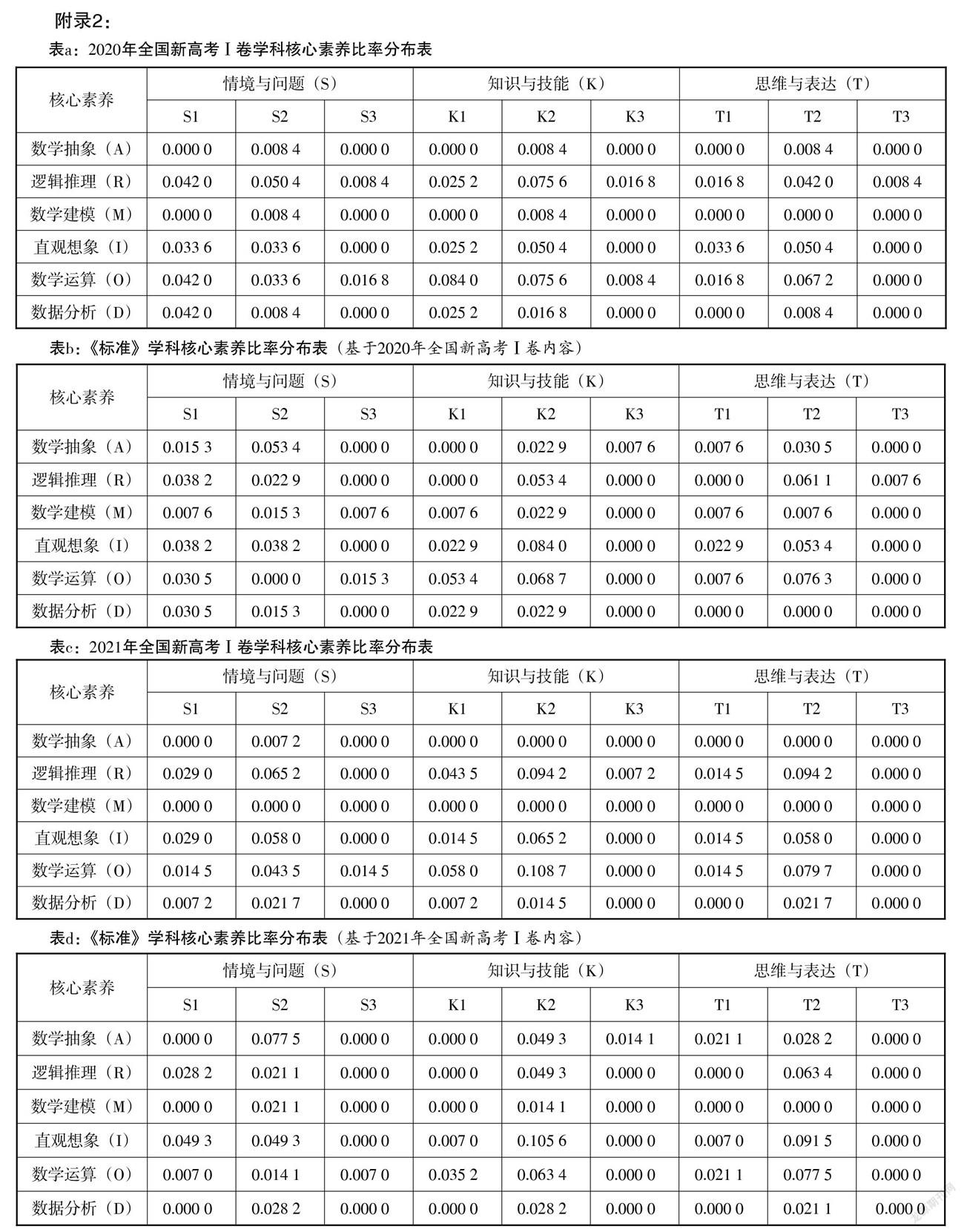
第三步：編碼完成后，統計六大核心素養在每一素養維度下所呈現的水平頻次，將統計數據放在“核心素養[×]素養水平”二維矩陣中進行標準化處理. 分別得到指向素養各方面的《標準》與2020年和2021年全國新高考Ⅰ卷的比率表（具體結果見附錄2）. 需要說明的是，由于數學學科核心素養的第四個方面（交流與反思）《標準》編碼皆為0，高考試題編碼亦為0，若對其進行一致性分析不具備參考意義. 因此，附錄及下文僅針對各素養的情境與問題、知識與技能、思維與表達三個方面進行一致性分析.

三、研究結果與分析

2020年和2021年全國新高考Ⅰ卷在原有全國卷的題型基礎上增加了多選題，試卷中每道試題都能對應到《標準》主要知識點的考查，且對應測查1 ～ 3個數學學科核心素養（如附錄1所示）. 總體而言，2020年和2021年全國新高考Ⅰ卷在試題內容分布上較為穩定，皆側重函數、幾何與代數主線，其次為概率與統計主線內容、預備知識，未有明顯變化. 因此，下文將聚焦核心素養視角進行數學新高考試卷與課程標準的一致性研究.

1. 總體一致性及其偏離地形圖分析

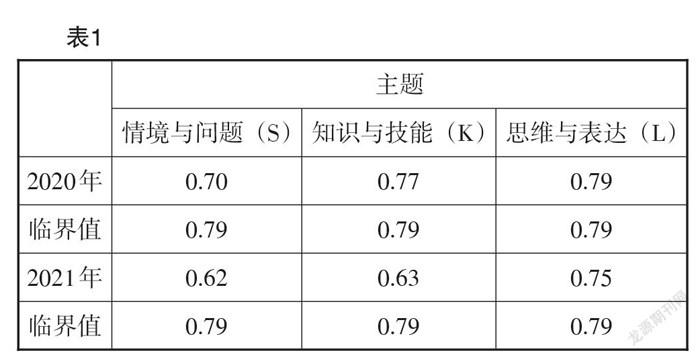
研究使用MATLAB軟件調用Porter一致性系數計算公式，分別計算核心素養指向下2020年和2021年全國新高考Ⅰ卷與《標準》的一致性系數[P]值及相應的一致性系數單側臨界值，結果如表1所示.

[ 主題 情境與問題（S） 知識與技能（K） 思維與表達（L） 2020年 0.70 0.77 0.79 臨界值 0.79 0.79 0.79 2021年 0.62 0.63 0.75 臨界值 0.79 0.79 0.79 ][表1]

兩年全國新高考Ⅰ卷與《標準》在素養指向下“情境與問題”“知識與技能”“思維與表達”三個方面的一致性系數皆依次上升，且均大于0.5，即分析對象之間都達到一定程度的一致性. 但僅2020年全國新高考Ⅰ卷與《標準》在學科核心素養的“思維與表達”方面，呈統計學意義上的一致性顯著.

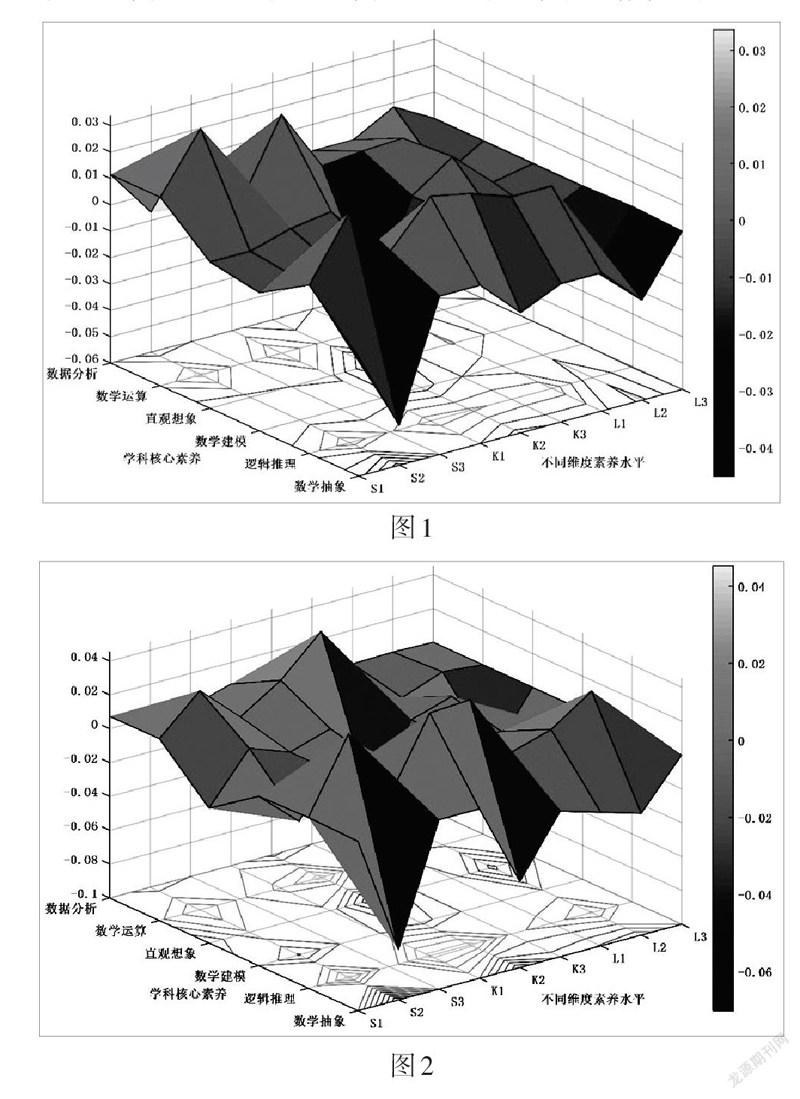
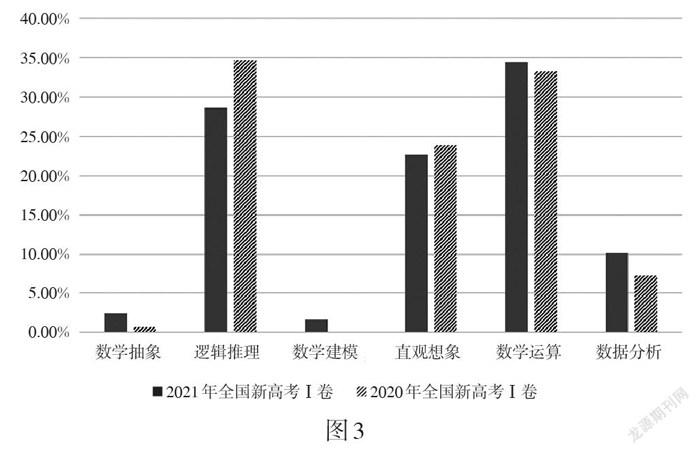
為進一步分析一致性顯著與否的原因，研究以《標準》為基準，將標準化處理后的矩陣相減得到差值，并以素養三方面各水平為[x]軸，以六大學科核心素養為[y]軸，差值為[z]軸，用MATLAB軟件分別畫出如圖1（2020年）、圖2（2021年）所示的一致性偏離地形圖.

當新高考試卷與《標準》之間的一致性良好時，偏離地形圖整體位置應處于零刻度線附近，且曲面平緩. 從圖1可以看出，2020年全國新高考Ⅰ卷與《標準》偏離地形圖中峰值主要出現在“情境與問題”區域，且集中于數學抽象、邏輯推理、數學運算素養的水平二與水平一. 從圖2亦可以看出，2021年全國新高考Ⅰ卷與《標準》偏離地形圖中峰值主要出現在“情境與問題”“知識與技能”區域，且集中于數學抽象、邏輯推理、直觀想象、數學運算素養的水平二. 兩年全國新高考Ⅰ卷中，邏輯推理、數學運算素養各方面的測查比重都高于《標準》，數學抽象素養各方面的測查比重皆低于《標準》. 其中，2021年全國新高考Ⅰ卷中數學建模素養各方面的測查比重低于《標準》.

上述分析表明，近兩年全國新高考Ⅰ卷整體符合《標準》的學業質量評價要求，但兩份試卷在各個素養的分布占比及變化、在素養“知識與技能”“情境與問題”方面的命題特征及變化有待深入分析.

2. 各素養測查占比兩年整體差異不顯著，皆側重數學運算、邏輯推理及直觀想象素養

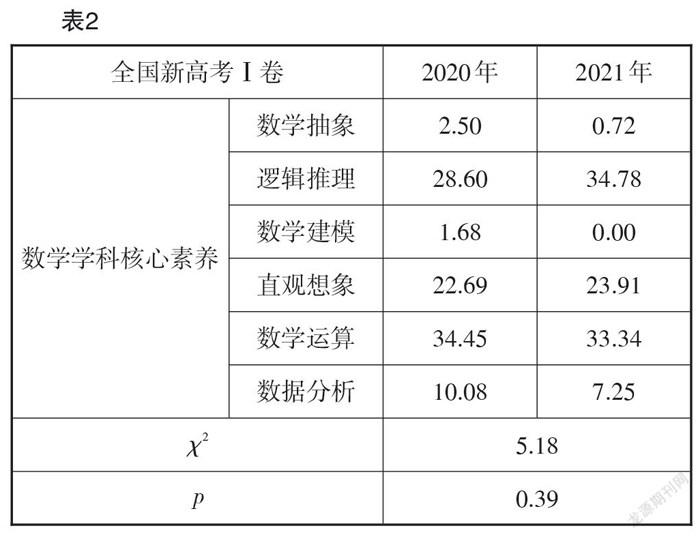
為進一步揭示六大核心素養測查的占比情況，研究繪制了如圖3所示的2020年和2021年全國新高考Ⅰ卷中測查的各個核心素養的分布圖，縱軸為各核心素養出現頻次的百分比.

從圖3可以看出，兩份試卷皆重點測查數學運算、邏輯推理及直觀想象素養，其占比均達到20%以上，且2021年全國新高考Ⅰ卷中邏輯推理、直觀想象測查比重較之2020年有所增加. 其次為數據分析素養，而數學抽象、數學建模素養的測查占比則均低于5%. 其中，數學建模素養測查僅在2020年全國新高考Ⅰ卷第6題中涉及，即新冠肺炎累計感染病例數模型分析，考查學生在熟悉情境中理解蘊含其中的數學問題，明晰模型中參數的意義以解決問題. 2021年全國新高考Ⅰ卷中并未出現對數學建模素養的測查.

研究運用R軟件，對2020年和2021年全國新高考Ⅰ卷中核心素養的分布占比（單位：%）進行一致性檢驗，得到卡方統計量及其[P]值，如表2所示.

卡方檢驗結果表明，2020年和2021年全國新高考Ⅰ卷中核心素養分布的整體差異不顯著（[χ2=5.18，p>0.05]），且均表現為數學運算素養測查比重最大（達30%以上），數學建模與數學抽象素養測查占比較低. 在兩份新高考試卷中，僅有兩道題涉及數學抽象素養測查：2020年全國新高考Ⅰ卷第4題以中國古代測定時間的儀器日晷為背景，需要學生通過數學抽象得到晷針與地球上過點[A]的水平面所成角的平面圖，進而分析計算線面夾角大小;2021年全國新高考Ⅰ卷第16題以我國傳統文化剪紙藝術為背景，考查學生通過數學抽象得到等比數列解決問題的能力. 其他試題雖然涉及現實情境，如2020年全國新高考Ⅰ卷第15題涉及勞動實習背景、2021年全國新高考Ⅰ卷第18題涉及“一帶一路”背景，但問題本身與情境聯系并不緊密，并不需要學生對情境中的數量關系或空間形式進行抽象.

3. 各素養測查水平兩年分布差異顯著，逐步趨向于學業質量水平二

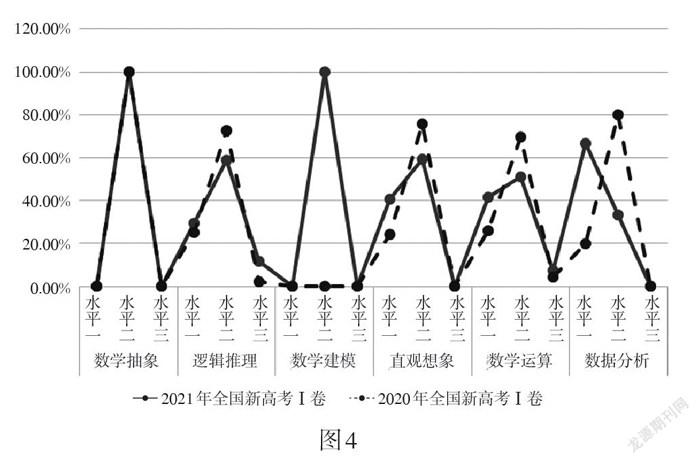
《標準》明確指出，學業質量水平二是高考的要求，也是數學高考命題依據. 研究以核心素養各水平占比為縱軸，繪制如圖4所示的2020年和2021年全國新高考Ⅰ卷中核心素養各水平分布圖. 由圖可知，兩份新高考試卷整體上核心素養的測查以水平二為主. 其中數學抽象、數學建模素養僅測查了水平二，如數學抽象素養主要考查學生能否在關聯情境中抽象出數學規則，其他水平層次均無體現;邏輯推理、直觀想象、數學運算素養均側重測查水平二，其次為水平一.

兩份試卷中數據分析素養的測查側重有所不同，2020年全國新高考Ⅰ卷側重測查素養水平一（占66.7%），其次為水平二（占33.3%）;而2021年全國新高考Ⅰ卷則強調數據分析素養水平二（占80%）的測查. 例如，2020年全國新高考Ⅰ卷第3題（場館志愿者安排）與第5題（學生體育項目喜好占比）的情境皆為學生熟悉的虛擬情境，學生只需識別相應概率模型即可解決問題，主要考查學生的數據分析素養是否達到水平一. 2021年全國新高考Ⅰ卷中減少了這類測查數據分析素養水平一的試題，增加了綜合測查數據分析素養水平二的試題，如第18題以學校組織“一帶一路”為背景，測查學生數據分析素養在情境與問題、知識與技能、思維與表達三個方面是否達到水平二，即需要學生在有關知識競答規則的情境中識別隨機現象，能選擇離散型隨機變量及其分布列刻畫隨機現象，并能用隨機變量期望值理解該結論的意義.

此外，兩份試卷中都涉及了對邏輯推理、數學運算素養水平三的測查，且皆出現在多選題及解答題的最后一題（壓軸題）中，但水平三占比逐年降低. 2020年全國新高考Ⅰ卷中兩道壓軸題都綜合測查了學生在邏輯推理、數學運算素養多個方面是否達到水平三. 例如，第12題（多選壓軸題）以信息論中信息熵為背景定義新問題，不僅需要學生識別基本的概率模型，測查學生是否具備基本的數據分析素養，更側重考查學生的邏輯推理、數學運算素養在情境與問題、知識與技能方面是否達到水平三，即學生需要在綜合情境中，用邏輯推理方法，理解信息熵的定義及運算法則，并能用新定義的運算程序，在多個選項中找到正確的數學命題. 2021年全國新高考Ⅰ卷中的兩道壓軸題則減少了對素養水平三的測查方面，主要測查學生數學運算素養在情境與問題方面是否達到水平三，如第12題（多選壓軸題）僅需要學生在有關正三棱柱的綜合情境中理解空間向量的運算法則.

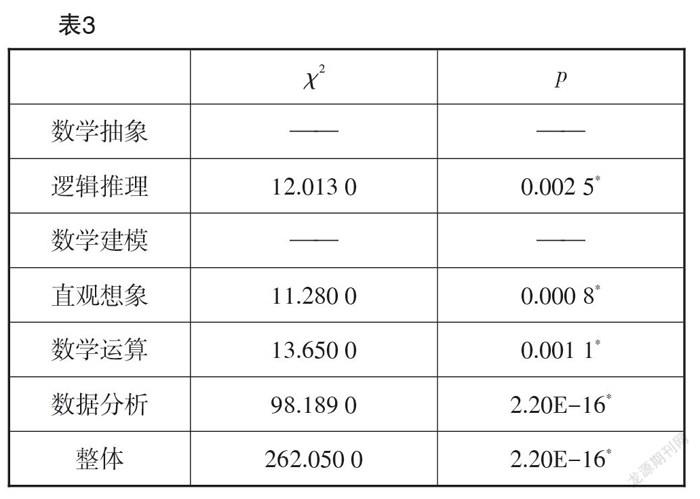
研究運用R軟件，對2020年和2021年全國新高考Ⅰ卷中各素養水平分布占比進行一致性檢驗，因兩份試卷中數學抽象素養測查均集中于水平二，2021年全國新高考Ⅰ卷未體現對數學建模素養的測查，因此不對數學抽象、數學建模素養進行卡方檢驗. 最終得到卡方統計量及其[P]值如表3所示. 2020年和2021年全國新高考Ⅰ卷在邏輯推理、直觀想象、數學運算、數據分析素養水平測查的分布上均存在顯著差異，表現為2021年全國新高考Ⅰ卷較之2020年全國新高考Ⅰ卷對核心素養水平二的測查比例有所提升，對水平一、水平三的測查比例有所減少.

4. 各素養測查維度皆缺失交流與反思，三大核心素養在其余三方面測查較為均衡

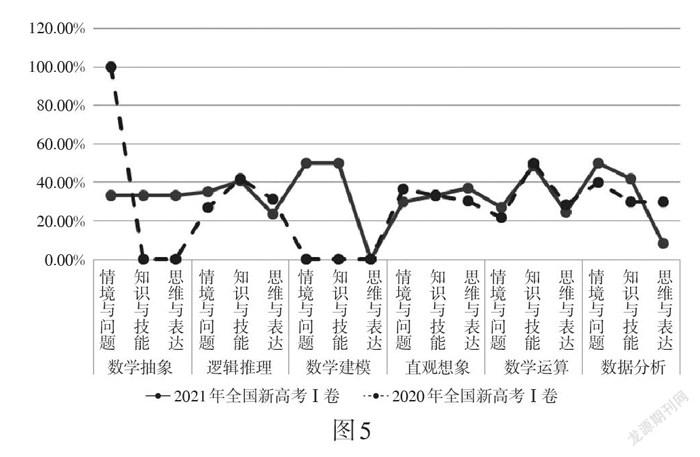
《標準》學業質量標準通過各素養的“情境與問題”“知識與技能”“思維與表達”“交流與反思”四個方面進行表述. 圖5呈現了2020年和2021年全國新高考Ⅰ卷中六大核心素養各方面的分布情況.

從圖5中可知，這兩份全國新高考Ⅰ卷均未涉及“交流與反思”維度的測查，核心素養測查維度的全面性、均衡性仍有待提升. 具體地，從素養各方面的占比來看，這兩份全國新高考Ⅰ卷對邏輯推理、直觀想象、數學運算這三大核心素養在“情境與問題”“知識與技能”“思維與表達”三方面測查皆較為均衡，占比區別較小. 數學抽象、數學建模素養在試卷中測查占比很小，其測查維度也呈現大幅的波動.

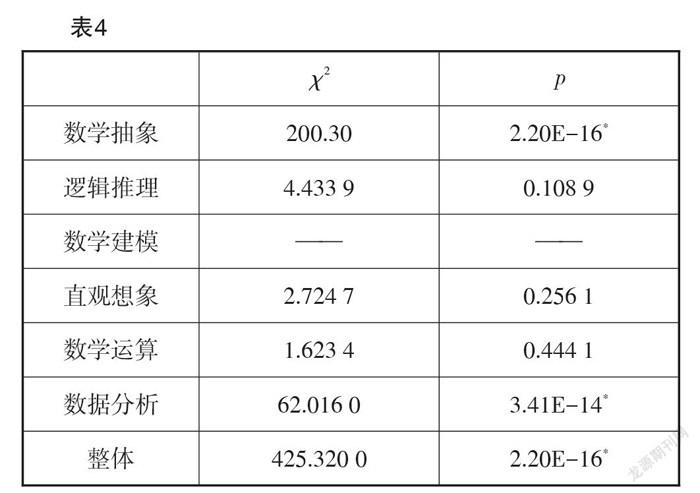
研究運用R軟件，對2020年全國新高考Ⅰ卷和2021年全國新高考Ⅰ卷中各素養水平分布占比進行一致性檢驗，因2021年全國新高考Ⅰ卷未體現對數學建模素養的測查，因此不對數學建模素養進行卡方檢驗. 最終得到卡方統計量及其[P]值如表4所示.

兩份試卷在邏輯推理、直觀想象、數學運算素養維度的測查占比不存在顯著差異. 但是在數學抽象、數據分析素養維度的測查比例存在顯著差異，表現為2021年全國新高考Ⅰ卷在數學抽象素養側重“情境與問題”維度，數據分析素養較之2020年全國新高考Ⅰ卷則更強調“思維與表達”維度，即能體會統計方法的思想，理解統計結論的意義.

四、研究結論與建議

《標準》學業質量標準聚焦學生數學學科核心素養的形成與發展，為高考命題提供了重要依據. 研究表明，2020年和2021年全國新高考Ⅰ卷都基本符合《標準》學業質量評價要求，且各素養測查逐步趨向《標準》所要求的學業質量水平二，即高考要求. 但新高考試卷中六大數學學科核心素養測查亦存在不均衡、整體性不足等問題，為促進教學、考評與《標準》形成合力，實現學生獲得高質量學業成就的最終目的，研究建議教學與高考測評如下.

1. 強化數學交流與反思，完善數學學科核心素養生成路徑

數學交流與反思是學生通過數學語言闡明自己問題解決的方法、過程和結果，分析和評價他人的數學方法和思想，需要學生在不斷深入的思考中進行評價、總結和拓展，是數學思維外顯化的可聽、可視過程. 交流與反思不僅是學生作為未來公民需要具備的基本素養，亦是數學學科核心素養形成的重要方面. 然而，數學交流與反思的測查要求在新高考試卷中卻鮮有體現. 一方面，由于高考命題主要參照了課程內容的要求，而內容要求中并沒有闡述“交流與反思”方面的要求;另一方面，可能受限于高考傳統命題形式. 傳統高考題型如選擇、填空或解答等，很難為學生提供交流與反思的機會. 因此，建議創新高考試卷命題形式，適當增加開放性、探究性問題，增設需要學生評析或比較自己和他人解題思路、方法的考查要求等. 在平時的教學中，亦可指導、鼓勵學生參與問題解決的交流與反思，并適時引入課題研究、調查報告等任務方式，引導學生在日常學習中逐步學會數學交流與反思，以完善學生數學學科核心素養的生成路徑.

2. 加強真實情境與問題的有機融合，實現數學抽象與數據分析素養的綜合性要求

學科素養是在特定學科情境（包括真實或有價值的虛擬情境）中解決問題、完成任務的能力和品質，素養的生成、表現與現實情境存在密切的內在關聯性. 研究結果顯示，2020年和2021年全國新高考Ⅰ卷中側重對核心素養的整合性考查，即在一道試題中測查多個數學學科核心素養，且以邏輯推理、數學運算等數學思考類素養居多，對數學運算素養的考查重點落在“能夠理解運算是一種演繹推理”這一類型. 新高考試卷中亦命制了與現實情境深度融合的范式. 例如，2020年全國新高考Ⅰ卷第6題給出新冠肺炎累計感染病例數模型，引導學生通過分析模型中的參數理解病毒感染的強度;2021年全國新高考Ⅰ卷第16題在傳統文化剪紙藝術中蘊含數列知識. 但是研究結果也顯示，由于試題情境大部分為學生熟悉的數學情境或虛擬情境，缺少真實情境的介入及其與問題解決的有機融合，兩份試卷中數學抽象素養測查比例較低，數據分析素養在2020年全國新高考Ⅰ卷中測查水平較低. 因此，建議在日常教學和測評命題中，以學科內容為載體，結合數學文化、社會時事、信息技術等背景，適度增設真實性、綜合性的教學或試題情境，將背景信息與數學知識有機融合，組織面向生活的教學，使教學融于生活而又超越生活，培植基于情境問題的核心素養.

3. 立足課程標準學業質量水平要求，觀照素養培育的個體性與層次性

學科核心素養指個體適應未來生活和終身發展所需的必備品格和關鍵能力. 個體差異性決定了素養評價需基于個體認知實現層次化測評，即合理控制試題難度，在測評過程中通過優化組合，衡量學生在不同素養水平層次的表現. 研究結果表明，新高考試卷均涉及了三個水平的素養測查，并呈現逐步趨向于課程標準所要求的學業質量水平二的高考要求，觀照了素養測查的個體性與層次性. 雖然高考在實踐中對教學的導向作用往往大于課程標準，但作為實踐環節的主體，教師若缺乏基于課程標準的教學實踐能力及評價素養，那么合力終究無法形成. 因此，建議教師基于數學新高考與課程標準建立起的有意義聯系，通過自學、培訓等途徑準確把握課程標準中學業質量水平要求;在教學中立足學科知識，基于學生個體化認知水平及核心素養的評價體系，設置梯度合理、具有結構差異性的教學任務，在使學生獲得個體發展的同時，推動素養導向的學業評價過程化，培養學生“真實性學力”的習得.

五、結束語

研究基于《標準》學業質量測評框架分析了近兩年數學新高考試卷與《標準》的一致性，雖然新高考試卷的課程內容與數學學科核心素養測評參照了《標準》的要求，但命題仍有待優化. 一線教師及高考命題者如何根據標準與評價框架，構建指向數學學科核心素養的測評及教學實踐機制，成為當前推進課程改革需迫切解決的課題.

參考文獻：

[1]中華人民共和國教育部制定. 普通高中數學課程標準（2017年版）[M]. 北京：人民教育出版社，2018.

[2]國務院辦公廳. 國務院辦公廳關于新時代推進普通高中育人方式改革的指導意見（國辦發〔2019〕29號）[EB/OL].（2019-06-11）[2021-06-28]. http：//www.gov.cn/zhengce/content/2019-06/19/content_5401568.htm.

[3]教育部考試中心制定. 中國高考評價體系[M]. 北京：人民教育出版社，2019.

[4]任子朝，趙軒. 基于高考評價體系的數學科考試內容改革實施路徑[J]. 中國考試，2019（12）：27-32.

[5]段志貴，黃云鶴. 基于高考評價體系的2020年新高考數學全國I卷分析與展望[J]. 中學數學雜志（高中版），2021（3）：48-55.

[6]朱立明，王久成. 基于數學學科核心素養測評框架的高考試卷分析：以2020年數學新高考Ⅰ卷為例[J]. 教育理論與實踐，2021，41（11）：16-21.

[7]邵朝友，張斌，王少非. 論學生學業成就評價與課程標準的一致性[J]. 教育研究與實驗，2011（6）：50-55.

[8]PORTER A C. Measuring the Content of Instruction：Uses in Research and Practice[J]. Educational Researcher，2002，31（7）：3-14.

[9]FULMER G W. Estimating Critical Values for Strength of Alignment Among Curriculum，Assessments and instruction[J]. Journal of Educational and Behavioral Statistics，2011，36（6）：381-402.

[10]張定強，裴陽. 新高考改革背景下數學試卷與課標一致性研究：以2017—2018年全國Ⅱ卷與浙江卷為例[J]. 數學教育學報，2019，28（4）：55-60.

[11]徐斌艷. 數學學科核心能力研究[J]. 全球教育展望，2013，42（6）：67-74，95.

[12]余文森. 論學科核心素養形成的機制[J]. 課程·教材·教法，2018，38（1）：4-11.

[13]常磊，鮑建生. 情境視角下的數學核心素養[J]. 數學教育學報，2017，26（2）：24-28.

[14]牛超. 實踐智慧視域下學科核心素養的生成[J]. 天津師范大學學報（基礎教育版），2021，22（3）：26-32.

[15]任子朝，陳昂，趙軒. 數學核心素養評價研究[J]. 課程·教材·教法，2018，38（5）：116-121.

[16]喻平. 基于核心素養的高中數學課程目標與學業評價[J]. 課程·教材·教法，2018，38（1）：80-85.

[17]邵光華，蔣周渠. 數學建模素養評價模型與案例分析[J]. 中國數學教育（高中版），2020（4）：3-10.

[18]鐘啟泉. 從“知識本位”轉向“素養本位”：課程改革的挑戰性課題[J]. 基礎教育課程，2021（11）：4-20.

3707501908208