高中數學建模教學的探索
馬云豪


[摘 要]數學建模素養是2017年版《普通高中數學課程標準》提出的六大數學核心素養之一.數學建模作為數學聯系實際的重要橋梁,作為數學應用的重要表現形式,在數學教學中越來越受到重視.探索數學建模教學能有效提升學生的數學素養.
[關鍵詞]數學建模;銀行貸款;核心素養
[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058(2021)05-0009-02
一、數學建模于數學教育的意義
2017年版《普通高中數學課程標準》中,首次提出了數學學科的六大核心素養,數學建模在列.數學建模是對現實問題進行數學抽象,用數學語言表達問題、用數學方法構建模型解決問題的素養.數學建模構建了“[提出問題→建立模型→解決問題]”的程序鏈.課程標準將數學建模的過程進行了細化解釋:在實際情境中從數學的視角發現問題、提出問題,分析問題、建立模型,確定參數、計算求解,檢驗結果、改進模型,最終解決實際問題.
數學建模作為數學與實際生活的橋梁,及數學應用的主要形式,正日益受到重視.
二、數學建模教學案例
基于以上認識,筆者選擇滬教版高一年級數列教學中的《銀行貸款問題》做了初步嘗試.
案例教學——銀行中的數學.
問題1:某銀行利率如表1,現馬老師向他人借了100萬元,打算整存整取存入銀行,
(1)按一年期定期儲蓄,到期后共可獲得多少錢?
[1 000 000×(1+1.75%)=1 017 500](元).
(2)按三年期定期儲蓄,到期后共可獲得多少錢?
[1 000 000×(1+2.75%)=1 027 500](元).
(3)按半年期定期儲蓄,到期后共可獲得多少錢?
[1 000 000×1+1.75%12×6=1 008 750](元).
設計問題1,以此來幫助學生復習存款問題,同時理解期數的概念,進而引入借貸問題.
問題2:馬老師最近打算購置新房,打算向他人借取100萬元,分期15年,逐月歸還,請你幫他計算一下,每個月需要還多少錢?
[1 000 000÷180=50 0009](元).
問題2的設計是希望學生能夠聯系實際,發現問題,意識到在借貸問題中還需要考慮利息因素,從而引出銀行貸款中的利率問題.
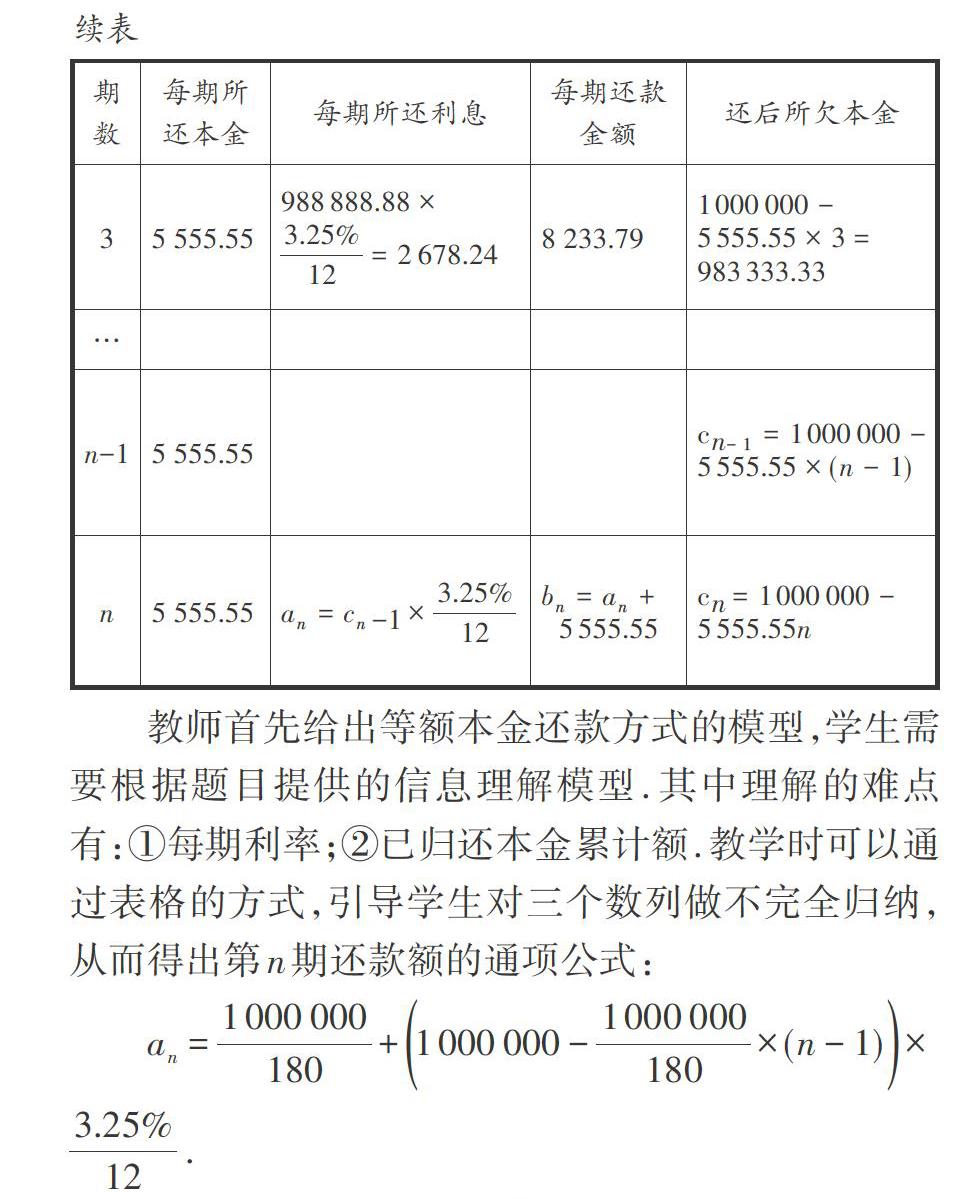
問題3:馬老師計劃向銀行申請公積金貸款100萬元,分期15年,共計180期歸還,公積金貸款年化利率為3.25%.銀行為馬老師提供了一種等額本金的還款方式,既在還款期內把貸款數總額等分,每月償還同等數額的本金和剩余貸款在該月所產生的利息.
每月還款金額= [貸款本金期數]+(本金-已歸還本金累計額)×每期利率.
(1)馬老師第一期需還款多少錢?
(2)馬老師第三期需還款多少錢?
(3)馬老師第n期需還款多少錢?
設數列[an]表示每期所還利息,數列[bn]表示每期還款金額,數列[cn]表示每期還款后所欠本金.
教師首先給出等額本金還款方式的模型,學生需要根據題目提供的信息理解模型.其中理解的難點有:①每期利率;②已歸還本金累計額.教學時可以通過表格的方式,引導學生對三個數列做不完全歸納,從而得出第n期還款額的通項公式:
問題4:馬老師每月工資為8 000元,無法承擔等額本金前期的還款金額,已知公積金貸款最高貸款額為100萬元,最長貸款年數為30年,貸款利率為3.25%,馬老師依然計劃申請公積金貸款,請你幫他設計一個貸款方案,每期需還款多少錢?
該問題的設計主要是希望學生體會到建模過程中如何確定和調整參數.
方案一:降低貸款總額,當貸款總額降低到96萬元,首期還款為7 933.33元,之后逐期減少,馬老師可以承擔.
方案二:延長貸款年限,當貸款年限為30年時,首期還款為5 486.11元,之后逐期減少,馬老師可以承擔.
問題5:馬老師依然覺得無法接受等額本金前期的還款金額,于是銀行提出另一種還款方式,既等額本息還款方式:在還款期內,每期償還同等數額的貸款(包括本金和利息),貸款的利息按復利計算.馬老師依然計劃申請公積金貸款100萬元,分360期歸還,公積金貸款利率為3.25%,則每期需還款多少錢?360期后總共還款多少錢?
問題5設計了生活中常用的等額本息的還款方式,是希望學生能從實際問題出發,分析問題,建立模型,從而解決實際問題.
在教學過程中,教師使用遞推法來幫助學生理解問題5.對問題5部分參數進行改變,進而探求一般化情況.
設第n期還款后欠銀行的本金為數列[an],初始值[a0]元(即貸款金額),每期利率為[β],總期數為m,每期需還款A元,則數列[an]滿足遞推公式:
三、對數學建模教學的反思
1.數學建模教學需要充分的鋪墊.本課時原計劃在一節課的時間內對等額本金和等額本息兩種還款方式都讓學生進行體驗和探索.而學生對相關知識的很多背景材料都很陌生,需要教師進行解釋,同時學生還需要對兩種還款方式進行計算求解,能有充足的時間參與到數學建模活動中.因此,在實際教學中,可將本課時的內容拆分成兩課時進行教學.因此,在數學建模教學過程中,對建模材料的鋪墊必須要充分,教師需要對時間有足夠的估計.
2.問題設計要與數學建模的環節有清晰的對應.教學設計中對問題的設計能對應到數學建模的某個環節,對數學建模活動進行分解,能針對某個環節進行訓練.如本課時中,進行了如下設計.
3.參數調整能夠有效地提升學生對建模的理解.如本課時問題4的設計,學生通過調整貸款總額和貸款年限進一步理解數學建模活動.實際上,數學建模是非常復雜的過程,數學建模教學需要區分與現有教學的區別.如果僅僅是面面俱到的教學,效果可能未必好.因此,建模教學可以仿照函數教學,對建模活動的每個環節進行分割,分步教學.
[? ?參? ?考? ?文? ?獻? ?]
[1]? 中華人民共和國教育部.普通高中數學課程標準(2017年版)[S].北京:人民教育出版社,2018.
[2]? 朱江紅.等比累進還款法與等額累進還款法的數學模型[J].滄州師范學院學報,2017(2):6-9.
(責任編輯 黃桂堅)

