對一道解析幾何題的探究
2021-03-30 00:44:24江蘇省淮陰中學教育集團淮安市新淮高級中學唐甜甜
數學大世界 2021年4期
江蘇省淮陰中學教育集團淮安市新淮高級中學 唐甜甜
在新課程標準的要求下,筆者認為,能夠使學生在學會知識的同時,自己發現問題、提出問題、分析問題并解決問題的課,堪稱一節好課。數學學習首先要學會研究題,因為很多習題的背后都有著非常豐富的研究價值,都應該是促進學生能力提升的道具,而不僅僅是去追求一個答案。能立足于學生的發展,引導學生主動發現問題、研究問題,才是教師促進學生提升能力的關鍵。本文從江蘇省淮陰中學和姜堰中學2019~2020 學年第二學期期中試卷的第22 題談起。
(1)求拋物線方程。
(2)過直線y=x-2上一點P(t,t-2)作拋物線的切線,切點為A,B。
①設直線PA,AB,PB 的斜率分別為k1,k2,k3,求證:k1,k2,k3成等差數列;
②若以切點B 為圓心,r 為半徑的圓與拋物線C 交于D,E 兩點,且D,E 關于直線AB 對稱,求點P 橫坐標的取值范圍。
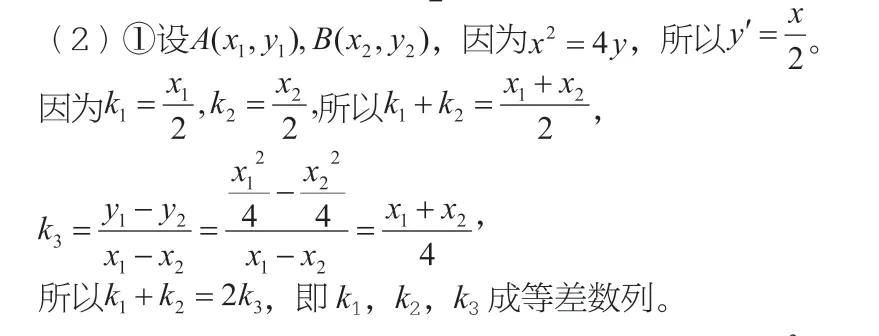

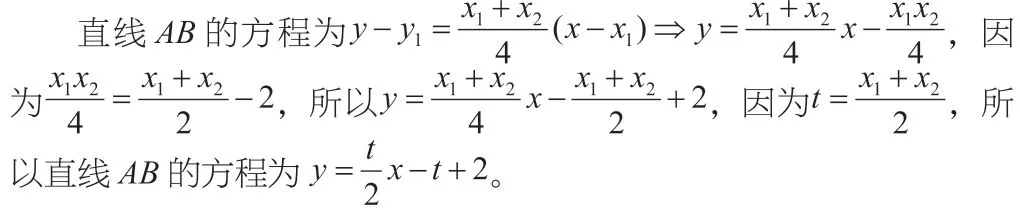
當t=0 時,拋物線上不存在兩點關于直線AB 對稱;
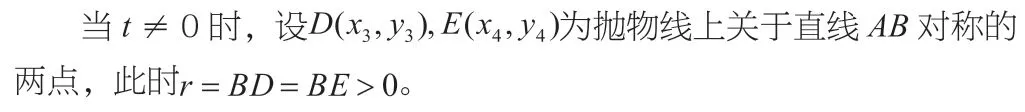

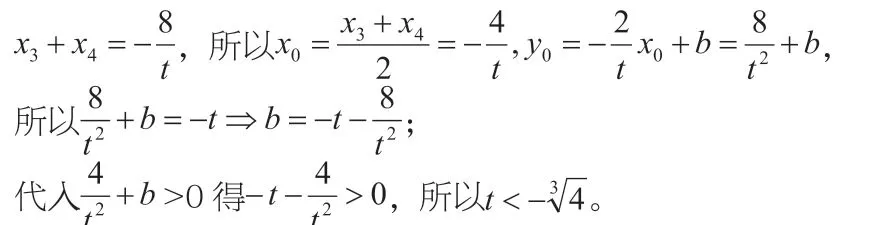
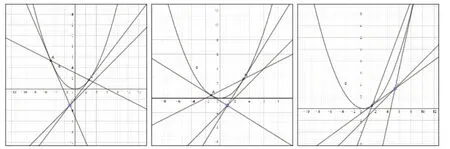
拓展:由以上圖像,我們還可以研究什么問題?
生:隨著點P 的變化,直線AB 也在變化,但是從以上圖像可以發現直線AB 過定點(2,2)。
師:參考答案中已經給出直線AB 的方程,是否還有其他方法求得直線AB 的方程?

師:是否存在點P 使得∠APB=90°?
生:當直線PA,PB 有一條直線斜率不存在時,不存在這樣的點P 使得∠APB=90°。

筆者繼續移動點P,引導學生發現問題,發現題目的價值。
生:還可以求得△PAB 面積的最小值。

猜你喜歡
語數外學習·高中版上旬(2024年18期)2024-02-20 00:00:00
體育科技文獻通報(2022年3期)2022-05-23 13:46:54
中學生數理化·中考版(2021年10期)2021-11-22 07:26:38
遼金歷史與考古(2021年0期)2021-07-29 01:06:54
科技傳播(2019年22期)2020-01-14 03:06:54
民用飛機設計與研究(2019年4期)2019-05-21 07:21:24
作文世界(小學版)(2018年4期)2018-10-16 17:13:34
中學生數理化·中考版(2017年10期)2017-04-23 06:29:38
中學生數理化(高中版.高二數學)(2017年1期)2017-04-16 05:33:44
快樂作文·低年級(2016年12期)2017-01-03 20:52:44

