構(gòu)造法在高中數(shù)學(xué)解題中的應(yīng)用

石豪方

【摘要】隨著我國(guó)基礎(chǔ)教育改革的不斷深入，為了積極響應(yīng)學(xué)生作為教學(xué)主體，以提升學(xué)生綜合學(xué)習(xí)能力為教學(xué)目標(biāo)的要求和號(hào)召，模式多元、內(nèi)容豐富的教學(xué)措施已經(jīng)普遍運(yùn)用到具體的教學(xué)中.其中，將構(gòu)造教學(xué)法合理地結(jié)合到高中數(shù)學(xué)中，能夠?qū)W(xué)生傳統(tǒng)的解題思路有效轉(zhuǎn)變，提升學(xué)生的數(shù)學(xué)解題能力.因此，本文針對(duì)構(gòu)造法的內(nèi)涵以及構(gòu)造法在高中數(shù)學(xué)解題中的有效應(yīng)用展開(kāi)了全面、詳細(xì)的分析.

【關(guān)鍵詞】構(gòu)造法;高中數(shù)學(xué);解題;應(yīng)用

構(gòu)造教學(xué)法主要指在高中數(shù)學(xué)教學(xué)過(guò)程中，教師引導(dǎo)學(xué)生根據(jù)具體數(shù)學(xué)題目中給出的已知條件以及與題目結(jié)論有關(guān)的內(nèi)容，構(gòu)造出一種與題目的條件或者結(jié)論一致的數(shù)學(xué)結(jié)構(gòu)模式，將題目中的未知條件轉(zhuǎn)變成已知條件，在此基礎(chǔ)上，通過(guò)更加簡(jiǎn)單的方式，正確解出題目.構(gòu)造法在高中數(shù)學(xué)解題中的有效應(yīng)用，不僅能夠幫助學(xué)生更快、更準(zhǔn)地解答數(shù)學(xué)問(wèn)題，還能將抽象的數(shù)學(xué)問(wèn)題具體化、形象化，使學(xué)生的創(chuàng)新思維得到進(jìn)一步的拓展和提升.

一、構(gòu)造法概述

（一）構(gòu)造法

構(gòu)造法就是將已經(jīng)掌握的知識(shí)以及方法進(jìn)行綜合性的使用，通過(guò)題目所給出的條件或結(jié)論所具有的特質(zhì)，構(gòu)造出新的滿足于條件或結(jié)論的數(shù)學(xué)形式.一般的解決問(wèn)題模式是對(duì)于題目所提供的條件或所求結(jié)論進(jìn)行全面的分析，并且通過(guò)創(chuàng)造性的思維構(gòu)造出函數(shù)、圖形、方程、數(shù)列等相關(guān)模型，最終達(dá)成有效轉(zhuǎn)化并得出結(jié)果.

（二）特征

構(gòu)造法在數(shù)學(xué)教學(xué)中是常用的，其在使用過(guò)程中有著明顯的特征：構(gòu)造性，通過(guò)構(gòu)造輔助性問(wèn)題，將原本的問(wèn)題進(jìn)行轉(zhuǎn)化;直觀性，利用構(gòu)造法進(jìn)行數(shù)學(xué)問(wèn)題的解決，其步驟較為直觀清晰;可行性，使用構(gòu)造法不僅可以有效判定數(shù)學(xué)對(duì)象，還可以在一定的步驟內(nèi)明確;靈活性，在開(kāi)展對(duì)某具體問(wèn)題的研究時(shí)，怎樣開(kāi)展構(gòu)造與學(xué)生的數(shù)學(xué)基礎(chǔ)和解題相關(guān)經(jīng)驗(yàn)有著緊密聯(lián)系;多樣性，構(gòu)造法與別的數(shù)學(xué)方法不同，在解題過(guò)程中通常會(huì)運(yùn)用到分析、綜合、觀察等多種手段.

（三）優(yōu)勢(shì)

構(gòu)造法在數(shù)學(xué)教學(xué)中的應(yīng)用優(yōu)勢(shì)在于可以將已知條件、未知條件和結(jié)論合理地關(guān)聯(lián)到一起，將原本的數(shù)學(xué)問(wèn)題簡(jiǎn)單化，也搭建知識(shí)的橋梁.同時(shí)，如果學(xué)生能夠有效地掌握構(gòu)造法，并在實(shí)際的解決問(wèn)題過(guò)程中進(jìn)行應(yīng)用，那么不僅會(huì)使學(xué)生解決問(wèn)題的能力得到提升，也能夠促進(jìn)學(xué)生多方面素養(yǎng)的發(fā)展.

二、構(gòu)造法在高中數(shù)學(xué)解題中的應(yīng)用

（一）構(gòu)造法在方程中的應(yīng)用

筆者對(duì)構(gòu)造法在高中數(shù)學(xué)解題中的有效應(yīng)用展開(kāi)的大量實(shí)際調(diào)查研究發(fā)現(xiàn)，在學(xué)生學(xué)習(xí)高中數(shù)學(xué)相關(guān)知識(shí)的過(guò)程中，要明確了解函數(shù)知識(shí)與方程之間的緊密聯(lián)系.在高中數(shù)學(xué)教學(xué)中運(yùn)用構(gòu)造法解決問(wèn)題時(shí)，方程法也是被普遍使用的解題措施之一，由于使用的頻率比較密集，因此，已經(jīng)成為目前高中生比較熟悉的解題方法之一.方程與函數(shù)之間存在著千絲萬(wàn)縷的聯(lián)系，大部分情況下，老師可以引導(dǎo)學(xué)生對(duì)題目中的已知條件進(jìn)行分析，詳細(xì)了解具體的結(jié)構(gòu)關(guān)系和數(shù)量特征，根據(jù)題目的內(nèi)容將假設(shè)法合理地結(jié)合其中，創(chuàng)建與題目?jī)?nèi)容一致的等量性方程式.在此基礎(chǔ)上，對(duì)方程式中各個(gè)量的特點(diǎn)、彼此之間的關(guān)系、方程式兩邊的等量關(guān)系進(jìn)行分析.同時(shí)，根據(jù)恒等式變形的原則，將抽象的函數(shù)內(nèi)容轉(zhuǎn)變成形象的幾何內(nèi)容和幾何圖形.這樣的教學(xué)方式，不僅能夠使學(xué)生對(duì)數(shù)學(xué)問(wèn)題有更加充分的理解，還能使學(xué)生解答數(shù)學(xué)問(wèn)題的速度和準(zhǔn)確性進(jìn)一步提升，從而為學(xué)生觀察能力、創(chuàng)新能力、邏輯思維能力的提升提供積極的幫助.舉一個(gè)簡(jiǎn)單的例子：

已知log123和log1215，求二者的大小關(guān)系.

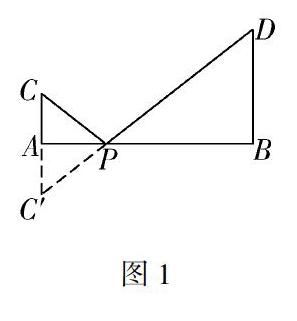
解析：根據(jù)題目知道，log123和log1215這兩個(gè)對(duì)數(shù)值都屬于靜態(tài)的函數(shù)值，因此，對(duì)這兩個(gè)對(duì)數(shù)值進(jìn)行對(duì)數(shù)函數(shù)構(gòu)造，就能得到一個(gè)對(duì)數(shù)函數(shù)的動(dòng)態(tài)函數(shù)值.構(gòu)造函數(shù)y=log12x，從而log123和log1215即是對(duì)數(shù)函數(shù)y=log12x中自變量x=3和x=15時(shí)的兩個(gè)函數(shù)值，這樣就實(shí)現(xiàn)了靜態(tài)函數(shù)值轉(zhuǎn)變成動(dòng)態(tài)函數(shù)值的目標(biāo)，從而得到log123

（二）構(gòu)造法在圖形中的應(yīng)用

在學(xué)生學(xué)習(xí)高中數(shù)學(xué)的過(guò)程中，運(yùn)用圖形是解決高中數(shù)學(xué)問(wèn)題普遍使用的方式之一.通過(guò)圖形解決數(shù)學(xué)問(wèn)題，不僅能夠?qū)⒕哂休^高復(fù)雜性的數(shù)學(xué)問(wèn)題得到簡(jiǎn)化，轉(zhuǎn)變成具體、形象的問(wèn)題，使學(xué)生能夠更加直觀地理解數(shù)學(xué)問(wèn)題，還能進(jìn)一步提升學(xué)生的數(shù)形結(jié)合能力，提升學(xué)生思維的靈活性.學(xué)生在明確題目的已知條件后，可結(jié)合已知條件構(gòu)造一個(gè)圖形，將抽象的代數(shù)問(wèn)題轉(zhuǎn)變成形象的幾何問(wèn)題，在此基礎(chǔ)上，結(jié)合代數(shù)與幾何的相關(guān)性質(zhì)定理，將代數(shù)問(wèn)題有效解答出來(lái).因此，加大培養(yǎng)學(xué)生靈活使用圖形構(gòu)造法的力度，能夠在很大程度上提升學(xué)生解決數(shù)學(xué)問(wèn)題的能力.比如：

已知1+x2+4+（4-x）2（0≤x≤4），求該代數(shù)式的最小值.

圖1解析：如果在解決這道代數(shù)問(wèn)題時(shí)單純地使用代數(shù)方式，那么難度極高，會(huì)使高中生產(chǎn)生較大的困擾.仔細(xì)觀察代數(shù)式的結(jié)構(gòu)特征可構(gòu)造一個(gè)直角三角形，將題目的內(nèi)容轉(zhuǎn)變成：一條直線上的某一個(gè)點(diǎn)到其他兩個(gè)點(diǎn)之間的最小距離，如圖所示.

已知AB=4，AC⊥AB，BD⊥AB，且AC=1，BD=2，P為AB上一點(diǎn).求P點(diǎn)到C點(diǎn)和D點(diǎn)之間的最小距離.

解析：設(shè)AP=x，則PC=1+x2，PD=4+（4-x）2.這樣，就將原問(wèn)題轉(zhuǎn)變成求P點(diǎn)在什么位置時(shí)，PC+PD的數(shù)值最小.畫一條以AB為中軸線的C點(diǎn)的對(duì)稱點(diǎn)C′，

將C′點(diǎn)與D點(diǎn)連接，與AB相交于點(diǎn)P，此時(shí)，根據(jù)△PAC′∽△PBD能得到等式x4-x=12，經(jīng)過(guò)計(jì)算，得到x=43.因此，通過(guò)簡(jiǎn)單的轉(zhuǎn)換就能得到P點(diǎn)到C點(diǎn)和D點(diǎn)之間的最小距離為5，也就是1+x2+4+（4-x）2（0≤x≤4）的最小值為5[2].

（三）構(gòu)造法在函數(shù)中的應(yīng)用

在高中數(shù)學(xué)知識(shí)體系的構(gòu)建中，函數(shù)是極為重要的知識(shí).函數(shù)構(gòu)造的學(xué)習(xí)對(duì)學(xué)生有效形成解題思路，加強(qiáng)解題能力有著關(guān)鍵性的作用.在開(kāi)展對(duì)高中生整體解題的教學(xué)中，教師的主要教學(xué)內(nèi)容就是讓學(xué)生形成一定的解題想法.實(shí)際上數(shù)學(xué)問(wèn)題中都蘊(yùn)含著函數(shù)思想.在代數(shù)、幾何等相關(guān)數(shù)學(xué)問(wèn)題的探析過(guò)程中，將有關(guān)問(wèn)題轉(zhuǎn)變?yōu)楹瘮?shù)問(wèn)題可以大大提升解題的效率，幫助學(xué)生形成一定的思維并深化學(xué)生的創(chuàng)新能力，不但增強(qiáng)了學(xué)生學(xué)習(xí)的主動(dòng)性，也鍛煉了學(xué)生的創(chuàng)造性思維.

（四）構(gòu)造法在數(shù)列中的應(yīng)用

在解決高中數(shù)學(xué)問(wèn)題時(shí)，數(shù)列構(gòu)造也是一種極為具有實(shí)用價(jià)值的解題形式.例如，等比數(shù)列、等差數(shù)列等都可以作為解答數(shù)學(xué)問(wèn)題的重要方法.在實(shí)際的解題過(guò)程中，教師可以通過(guò)構(gòu)造法將數(shù)學(xué)問(wèn)題轉(zhuǎn)變?yōu)閷W(xué)生所熟悉的等比數(shù)列，這樣學(xué)生在解答時(shí)相對(duì)較為簡(jiǎn)單，有利于學(xué)生對(duì)數(shù)學(xué)知識(shí)的理解以及運(yùn)用.

三、構(gòu)造法運(yùn)用于高中數(shù)學(xué)解題中的策略

（一）形成構(gòu)造理念

有效運(yùn)用構(gòu)造法的前提條件是了解以及掌握構(gòu)造法的真正含義.構(gòu)造是采取一系列的措施，經(jīng)過(guò)一定的流程以及步驟達(dá)成相應(yīng)的目的.教師在為學(xué)生講解構(gòu)造法時(shí)，一定要以簡(jiǎn)單的、學(xué)生容易理解的形式，讓學(xué)生通過(guò)自己理解和認(rèn)知，采取合適的形式提高解決問(wèn)題的效率，進(jìn)而鍛煉學(xué)生的思維.使用構(gòu)造法可以將原本難以解決的問(wèn)題構(gòu)造為平時(shí)已經(jīng)解決的簡(jiǎn)單問(wèn)題，從而高效地完成相應(yīng)的學(xué)習(xí)任務(wù)，并掌握知識(shí)內(nèi)容.以方程為例，方程主要包括代數(shù)方程、曲線方程等，涉及的知識(shí)面極為廣泛，而且對(duì)于學(xué)生來(lái)講難度較大，不易精準(zhǔn)高效地掌握.方程與函數(shù)、代數(shù)式等相關(guān)數(shù)學(xué)知識(shí)有著密切的關(guān)聯(lián)，所以學(xué)生在解答疑難方程式的過(guò)程中合理采用構(gòu)造法，可通過(guò)方程式的相應(yīng)理論、性質(zhì)等進(jìn)一步強(qiáng)化對(duì)知識(shí)的記憶，理解數(shù)學(xué)知識(shí)內(nèi)容，進(jìn)而轉(zhuǎn)化出更多的題目，解決更多的難題.高中生會(huì)通過(guò)自身的不斷剖析與反思，逐步將生活中的數(shù)學(xué)知識(shí)融入高中數(shù)學(xué)知識(shí)的學(xué)習(xí)中，自己創(chuàng)造更多的學(xué)習(xí)機(jī)會(huì)，促進(jìn)良好學(xué)習(xí)習(xí)慣的形成.

（二）結(jié)合解題方式

在高中數(shù)學(xué)教學(xué)中，解題方式多樣，構(gòu)造法只是其中一種高效的解決形式，并不適用于所有的數(shù)學(xué)問(wèn)題，還需要與其他的解決方式進(jìn)行一定的結(jié)合，才能夠發(fā)揮最大的成效，真正做到將疑難問(wèn)題簡(jiǎn)單化.例如，在解決方程、函數(shù)、不等式、絕對(duì)值等問(wèn)題時(shí)，最基本的思路都是將絕對(duì)值轉(zhuǎn)化為不含絕對(duì)值的問(wèn)題，其中運(yùn)用分類討論、幾何意義等方式能夠在實(shí)際的解題過(guò)程中將自己的思維進(jìn)行一定的轉(zhuǎn)變，將題目中的條件以及概念、性質(zhì)等進(jìn)行有效的解析，在最短的時(shí)間明確最合適的解決思路，選擇最有效的解決方法，進(jìn)而高質(zhì)量地解決疑難知識(shí)點(diǎn).將多種解決問(wèn)題方式進(jìn)行一定的結(jié)合，不僅可以實(shí)現(xiàn)解決問(wèn)題成效的提升，還能夠鍛煉學(xué)生的思維，使學(xué)生在學(xué)習(xí)過(guò)程中逐漸形成自主學(xué)習(xí)的相關(guān)能力.

（三）促進(jìn)多向思維

從初中到高中，數(shù)學(xué)知識(shí)相對(duì)以往更具抽象性，而且內(nèi)容復(fù)雜.若是學(xué)生還是一成不變地采用固有的思維方式去學(xué)習(xí)新的數(shù)學(xué)知識(shí)和思考新的數(shù)學(xué)問(wèn)題，則很難將其中的知識(shí)點(diǎn)高質(zhì)量地掌握，從而無(wú)法在實(shí)際的學(xué)習(xí)過(guò)程中進(jìn)行運(yùn)用.所以教師在開(kāi)展數(shù)學(xué)知識(shí)的教學(xué)過(guò)程中，一定要注重對(duì)學(xué)生多向思維的培養(yǎng)，讓學(xué)生將固有思維的局限性打破，合理地使用構(gòu)造法，還要運(yùn)用概括法、類比法等多種思維模式將數(shù)學(xué)問(wèn)題中隱含的關(guān)系、條件等有效提取，從而構(gòu)造數(shù)學(xué)解題模式，讓解題變得更靈活且多樣，促使學(xué)生高質(zhì)量地解決問(wèn)題，思維向更全面的方向發(fā)展.

（四）養(yǎng)成轉(zhuǎn)化思維

若學(xué)生在學(xué)習(xí)知識(shí)的過(guò)程中無(wú)法通過(guò)直觀的概念進(jìn)行一定的引領(lǐng)，在探究本質(zhì)上則較為困難，因此，教學(xué)時(shí)一定要運(yùn)用數(shù)形結(jié)合這一理念，通過(guò)數(shù)字與圖形的有機(jī)結(jié)合，幫助學(xué)生以最快的速度發(fā)現(xiàn)解決問(wèn)題的方式.在教學(xué)中，教師要引領(lǐng)學(xué)生形成一定的轉(zhuǎn)化思想，讓學(xué)生可以對(duì)不同類型的問(wèn)題進(jìn)行合理的分析，形成一定的學(xué)習(xí)習(xí)慣，促使學(xué)生更愿意思考，從而提高思維能力及創(chuàng)造能力.

四、結(jié)束語(yǔ)

根據(jù)以上針對(duì)構(gòu)造法在高中數(shù)學(xué)解題中的有效應(yīng)用展開(kāi)的詳細(xì)分析，我們能夠更加明確地了解，對(duì)于高中生而言，各科的學(xué)業(yè)壓力都比較大，因此，在解決難度較大、數(shù)量較多的數(shù)學(xué)問(wèn)題時(shí)，很難保持較高的積極性和主動(dòng)性.鑒于此，為了將學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)的主觀能動(dòng)性充分激發(fā)出來(lái)，教師將構(gòu)造教學(xué)法合理地結(jié)合其中，將數(shù)學(xué)問(wèn)題簡(jiǎn)化的同時(shí)，使學(xué)生思維方式更靈活，從而使高中數(shù)學(xué)教學(xué)質(zhì)量和效果提升到一個(gè)新的高度.

【參考文獻(xiàn)】

[1]楊燕.淺析構(gòu)造法在高中數(shù)學(xué)解題中的應(yīng)用[J].讀與寫（教育教學(xué)版），2016（9）：112-114.

[2]王志寶.高中數(shù)學(xué)解題教學(xué)中如何巧用構(gòu)造法[J].赤子（上中旬），2015（18）：317-319.