滲透數學思想方法，形成可持續發展的學習能力

崔燕珊

【摘要】數學思想方法作為數學的精髓，蘊含在數學內容當中，與數學知識相互滲透、相互聯系。對于數學思想方法的研究既要從理論中認識與學習，又要從教學實踐中應用與灌輸。時代在召喚數學思維能力強者，數學科學的可持續發展已然成為主流。本文主要探究小學數學思想方法及其教學策略，并主要分為以下幾個部分：（1）數學思想方法的研究意義;（2）小學數學典型思想方法分析;（3）小學數學思想方法教學實踐的原則。

【關鍵詞】小學數學;數學思想方法;教學實踐原則;可持續發展學習能力

荷蘭數學家，數學教育家弗萊登塔爾（Hans Freudenthal）曾提出，“與其說學數學，倒不如說學會數學化。”數學化是一個過程，只要現實世界在一系列因素的影響下進行著變化、延拓和深化，這個過程就在持續著。這些因素也包括著數學，而且數學反過來被變化著的現實所吸引。縱使數學知識內容瞬息萬變，但數學的本質數學思想方法卻始終灌輸其中。隨著新課標改革推行、生本教育理念提出，數學教育對發展學生的數學思維能力日益重視，教學模式逐漸從“授之以魚”向“授之以漁”模式的轉變。

一、數學思想方法的研究意義

1.發展學生數學思維，形成可持續發展的自學能力

數學思維就是用數學的觀點去思考問題和解決問題的能力，可持續發展的學習能力則是指學生終身學習和終身發展所需要的主體探究精神與能力。好的數學思想方法學習可提高學生的思維水平，優化思維品質，真正懂得數學的價值，建立科學的數學觀念，并形成良好的個性品質及科學世界觀和方法論，為自身可持續發展奠定良好的基礎。

2.形成良好的數學認識結構，能自主建構知識體系

數學認識結構是指人們根據自己的經驗，將數學知識按照自己理解的廣度和深度，結合自己的感覺、知覺、記憶、思維、聯想等認知特點組合成一個具有內部規律的整體結構。數學認識結構的形成，是人們通過數學認知活動后，數學知識結構在大腦中的內化。這個內化過程是一個動態的、發展的過程。數學思想方法滲透在各個知識當中，在教學活動中得以體現，又促進學生理解知識的本質與規律，促進學生把握各個知識點之間的聯系，有利于知識架構的形成，利于數學知識的系統性把握，進一步優化數學認識結構。

3.營造素質教育的教學氛圍，提高教師的自身素質

新課程改革的全面開展與實施，帶來了全新的教育理念，對于教師也賦予了新的時代要求，即樹立現代教育理念，樹立新的教師觀，樹立新的學生觀。教學理念的現代化，不僅是教學內容的現代化，更注重數學思想、方法以及教學手段的現代化。因此，教學中滲透數學思想方法成為了實現現代化的關鍵。這也迫使教育者不斷鉆研以提高自身的教學水平。

二、小學數學中的數學思想方法分析

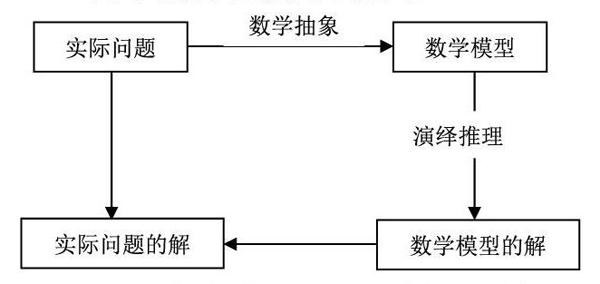
基本數學思想是體現或應該體現于基礎數學中的具有奠基性、總結性和最廣泛的數學思想，它們含有傳統數學思想的精華和現代數學思想的基本特征，并且是歷史地發展著的。小學數學發展所依賴的思想本質上有三個，它們構成數學的基本思想，分別是抽象思想、推理思想、模型思想。

1.抽象思想

數學的本質屬性就是抽象。數學中的抽象指的是把人們日常生活和社會實踐中那些與數學相關的東西吸取出來，去掉事物中感性的部分，得到數學研究的對象，比如數、點、線、面等等。這些抽象的結果在經歷了從現實到數學、從數學到高層次的數學逐層次抽象后，變得不再是事物的本身，因此，數學研究的是這些東西之間的關聯。

對于小學數學，抽象的內容在本質上有三種：（1）數量與數量關系的抽象;（2）圖形與圖形關系的抽象;（3）隨機關系的抽象。其中，數量關系是小學數學中的基礎，主要研究事物內在因果性、規律性、關系性，以數及其運算為主。圖形關系主要以討論圖形的直覺和直觀為主，其關系的核心在于分類，如，三角形、立方體、抽對稱圖形等。隨機關系則是建立在這些抽象基礎上的建構性抽象，一般須讓學生親身經歷數據的收集、整理和決策，如，質數和合數。

以數量關系中“數的產生與十進制計數”為例，簡述抽象思想。抽象源于生活，數的產生就是從具體形象結繩計數、刻道計數，抽象到阿拉伯數字1，2，3…這是從實物抽象出與數學相關的代表性例子——數字，其本質只有大和小。“大小關系”這一本質得到抽象與具體后，又可以對“序的關系”進行抽象。隨著數的量變，以“一”為計數單位的計數方式不再被滿足，便出現了以“十”為計數單位的計數方式，這是抽象思維的層次性體現。教科書中以10根小棒捆起來的方式呈現，就是把“10”抽象為“一”。以此類推，以“滿十進一”的方式得到后繼數，產生了數位順序表，繼而形成了無限的正整數序列：1，2，3…，n，…，數的產生就是逐步抽象的思維過程。

縱觀整個小學數學知識網絡，抽象思想在數學及教學過程中無處不在。滲透抽象思想，需立足于現實，喚起學生的生活體驗，層次性地揭示其本質，只有根據其特點，才更有效地傳遞給學生。

2.推理思想

數學自身的發展依靠的是推理。推理是從一個或幾個已有的判斷得出另一個新判斷的思維形式。小學數學中的推理主要分為兩種形式：演繹推理和合情推理。命題范圍由大到小的是演繹推理，反之則是合情推理。三段論、假言推理、選言推理、關系推理等是演繹推理中常見的幾種形式，而合情推理常見形式有：歸納推理和類比推理等。

推理思想一般體現在四個領域：數與代數、圖形與幾何、統計與概率、綜合與實踐。例如，學習3的倍數特征，通過列舉3的倍數的數字，發現規律，歸納出結論，是由特殊到一般，屬于歸納推理;當我們運用3的倍數的特征去判斷一個數是不是3的倍數，這是演繹推理的思想。再舉一個蘊含類比推理思想方法的例子。

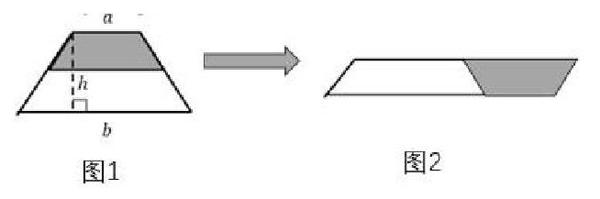
例1：下圖是推導梯形面積時教材提供的一種方法。

請用圖1中的字母表示圖2中的底、高與面積，則圖2的底是_____，高是_____，面積是_____。本題考查的就是學生推理思想方法的應用能力，利用長方形的面積公式，推導梯形的面積。