小學數學教學中的思辨能力培養

吳佳佳

摘要：思辨能力就是思考、辨析的能力，問題的引領則是思辨能力生長的重要動力。在小學數學課堂中，可以通過循序漸進的設問、“大問題”統領的追問、多角度的“質問”，著力培養學生的思辨能力。

關鍵詞：思辨能力;小學數學;設問;追問;“質問”

思辨能力就是思考、辨析的能力，思考指的是推理、判斷等思維活動，辨析指的是對事物的情況、類別、道理等的辨別分析。“問題是數學的心臟。”在小學數學課堂中，可以通過循序漸進的設問、“大問題”統領的追問、多角度的“質問”，著力培養學生的思辨能力。

一、于循序漸進的設問中培養

數學教學應該是促進學生思考、啟發學生智慧的過程。教師要對教學有全局的把握，通過循序漸進的設問，引導學生不斷地思考、辨析，喚醒思辨意識，培養思辨能力。

例如，教學《釘子板上的多邊形》一課時，教師設置了如下問題：

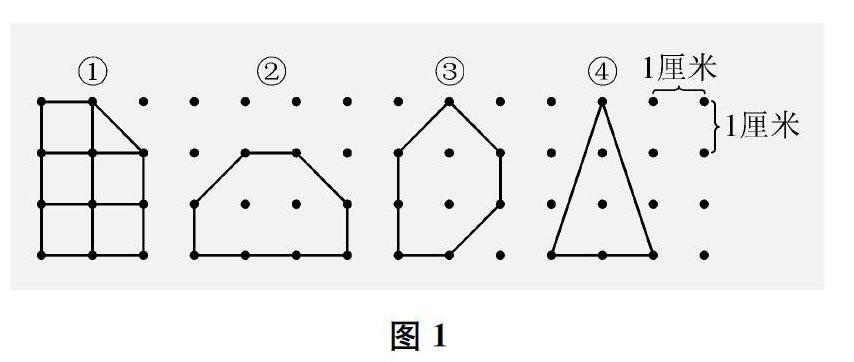
1.如圖1所示，請大家觀察這些多邊形，它們的內部都有2個釘子，那它們有什么不同呢？

2.觀察表1中的數據，多邊形的面積和邊上的釘子數之間有沒有關系？有怎樣的關系呢？

（平方厘米）①95.5②85③74.5④433.內部釘子數是2的多邊形的例子舉得完嗎？我們能不能找到一個反例，證明這個規律不存在呢？

這里，教師沒有直接出示表格，而是通過提問先讓學生聚焦特征，思考發現規律的第一步要做什么，辨析哪些特征可能會和規律有關，把看似不相干的數字聯系起來;接著，再讓學生思考、探索，明白規律的發現、觀點的得出是需要證據來支撐的;在探索出規律后，繼續讓學生尋找反例，促使學生在強化思考過程嚴密性的同時充分認識規律的外延，持續地思辨。

二、于“大問題”統領的追問中培養

思辨能力的一個重要表現是，能進行有邏輯、有條理的思考，進而做到層次分明、條理清楚的分析。“大問題”統領的追問對學生這一表現的達成有很好的推進作用。

例如，教學《整數除以分數》一課時，教師在“整數除以分數怎么算？”這個“大問題”的統領下，有層次地追問“為什么”“怎么驗證”“還有什么”，指引學生經歷思辨的過程：

教師出示“4÷25”，指名學生口算，根據學生回答課件呈現：4÷25=4×52=10。教師追問：同意嗎？反思一下，為什么這么做？學生回答：因為25÷4=25×14，所以4÷25=4×52。教師追問：能舉例子來驗證這樣的算法嗎？學生用畫圖的方法舉例：小明25小時走了4千米，他平均每小時走多少千米？如圖2所示，4÷25=4÷2×5=10（千米）。教師追問：還有其他方法嗎？學生交流：（1）4÷25=4÷0.4=10;（2）4÷25=205÷25=10;（3）4÷25=4×5÷25×5=10。

整數除以分數的算法，學生很容易掌握，而對于為什么這樣算（算理），學生則“心求通而未達，口欲言而未能”。于是，教師通過“大問題”統領的追問，不斷引導學生溝通算法之間的聯系。在層級遞升的追問中，學生不但加深了對知識點的理解，還經歷了充實的思辨過程，培養了思辨能力。

三、于多角度的“質問”中培養

這里的“質問”指質疑地問，是指建立在良好的判斷之上，用合理的、開放的方式對別人或自己已有的觀點、方法進行辨析。通過多角度的“質問”，學生能綜合不同維度、向度的思考得出結論，獲得數學知識本質的透徹理解，走向深刻思辨。

例如，教學《認識小數》一課時，教師設置了如下問題：

1.我們剛剛測量了兩個長方形的長和寬（如圖3、圖4所示），都用分米作單位時，為什么第一個長方形的長和寬可以用整數來表示，第二個長方形的長和寬卻要用分數來表示？

2.既然可以用厘米表示，為什么要用分數呢？既然有了分數，為什么還要有小數呢？

3.既然叫“小數”，它一定很小嗎？

為什么用分數表示？既然有了分數，為什么還要引入小數？這些問題引導的是學生對小數價值的探尋，即與分數相比，小數有什么特別之處。小數一定很小嗎？這一問題引導學生完善對小數的認識——小數包含整數部分和小數部分，整數部分大的話，小數也就大。將來還有可能認識什么樣的數呢？這是學生自發生成的“質問”，是他們自主思辨意識的體現，表明了他們思辨能力的發展。

參考文獻：

[1] 陳士文.“智慧數學”之數學改造[M].南京：江蘇鳳凰教育出版社，2016.

[2] 胡彩云.《釘子板上的多邊形》教學設計及思考[J].小學教學設計，2019（32）.