2021 年新高考全國數學卷導數試題分析與探究

李海北

（廈門雙十中學，福建 廈門 361009）

2021 年教育部考試中心共命制了兩套不分文理的新高考數學試卷，兩套試卷的壓軸題都是導數應用的試題，體現了對函數主線的重點考查.導數試題除了考查常規的函數單調性外，重點考查了函數零點個數和函數極值點偏移問題.

一、函數零點個數問題

研究函數f(x)的零點個數，一般是先確定f(x)的單調區間.如果f(x)在區間D 內單調，且在區間D 內存在x1、x2，滿足f(x1)＜0,f(x2)＞0，那么f(x)在區間D內有唯一零點.而對于含參數的函數f(x)，除了可以直觀判斷的一些特殊點外，要在區間D 內直接找到x1和x2常常是很困難的.如果將f(x)中的指數函數或對數函數放縮為冪函數，并保持放縮后的新函數在區間端點的極限不變，再通過放縮后的函數找“點”，難度就大大降低了.

不難證明下列不等式，它們可用于函數的放縮.

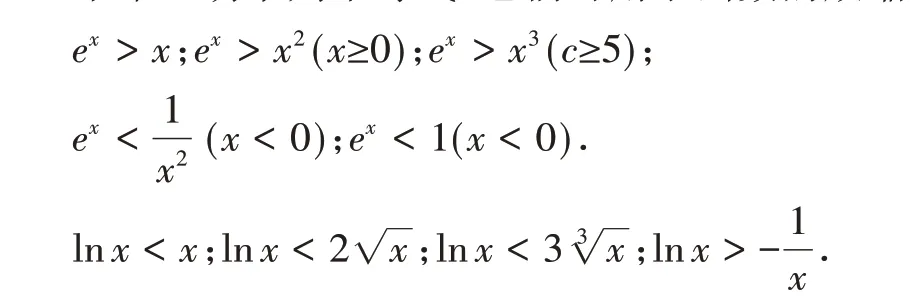
依此類推，可以得到更多的不等式.當然，在解答題的求解過程中，用這些不等式必須先給出證明.

例1（2021 年新高考全國Ⅱ卷第22 題）已知函數f(x)=(x-1)ex-ax2+b.

（1）討論函數f(x)的單調性；

（2）從下面兩個條件中選一個，證明：f(x)有一個零點.

分析與探究第（1）題是常規題.對于第（2）題，若選①，由（1）知，f(x)的增區間是(-∞,0)，(ln 2a,+∞)，減區間是(0,ln 2a).

因為b＞2a＞1，所以f(0)=-1+b＞0（x=0 是可以看出一個特殊點）.要證明f(x)有一個零點，一是要證明f(x)的極小值f(ln 2a) ＞0，二是要找到一個x0∈(-∞,0)，滿足f(x0)＜0.

f(ln 2a)=(ln 2a-1)·2a-a·(ln 2a)2+b＞2a·ln 2a-2a-a·(ln 2a)2+2a=a·ln 2a·(2-ln 2a)≥0.

當x→-∞時，對f(x) 的值起主要作用的是-ax2→-∞，而(x-1)ex→0-，可以把它略去.即當x∈(-∞,0)時，(x-1)ex＜0，f(x) ＜-ax2+b.

若選②，證明的難點仍然是找到一個x0∈(0,+∞)滿足f(x0)＞0.

注意到當x→+∞時，(x-1)ex要遠比ax2大，可以考慮將ex縮小為xn，并確保(x-1)xn要遠比ax2大，所以x＞1 且n=2 即可.

當x＞1 時，ex＞x2，

f(x) ＞(x-1)x2-ax2=x2(x-1-a)+b，

當x≥2+a時，x2＞1，f(x) ＞x-1-a+b.

取x0=max{2+a,1+a-b}∈(0,+∞)，則f(x0)＞0.

例2（2021 年新高考全國Ⅰ卷第7 題）若過點(a,b)可以作曲線y=ex的兩條切線，則

A.eb＜aB.ea＜bC.0 ＜a＜ebD.0 ＜b＜ea

分析與探究本題的實質也是零點個數問題.

設切點為(x0,ex0)，則切線方程為y-ex0=ex0(x-x0).因為切線過點(a,b)，所以b-ex0=ex0(a-x0)，即(x0-a-1)ex0+b=0.

于是可以作兩線切線的充要條件是：

函數h(x)=(x-a-a)ex+b恰有兩個零點.

因為h′(x)=(x-a)ex，所以h(x)在(-∞,a)上遞減，在(a,+∞)上遞增.

h(x)極小值=h(a)=-ea+b＜0，即b＜ea.

下面證明當0 ＜b＜ex時函數h(x)恰有兩個零點.

可以看出，h(a+1)=b＞0，h(x)在(a,+∞)內有唯一零點.

當x→-∞時，(x-a-1)ex→0-，h(x) →b＞0.但要證明，還是要找到一個x1∈(-∞,a)，滿足h(x1)＞0.

作為選擇題，如果學生清楚切線的定義，理解當割線的兩個交點無限接近時，割線無限趨近的確定位置就是切線，那就可以不必通過運算推理，結合圖形就能得到點(a,b)在曲線y=ex與x軸之間.

近年高考常考查函數零點的個數問題，其難點也都是如何找“點”.下面就近年一些高考試題求解過程中涉及找“點”的部分說明如何先放縮再找“點”.

例3（源自2016 年新課標全國Ⅰ卷理第21 題）已知函數f(x)=(x-2)ex=a(x-1)2.當a＞0 時，證明：存在x1∈(-∞,1)，f(x1)＞0；當a＜0 時，證明：存在x2∈(1,+∞)，f(x2)＞0.

分析與深究當a＞0,x＜0 時，ex＜0，(x-2)e3＞x-2，所 以f(x) ＞x-2+a(x-1)2=ax2-2ax=a+x-2 ＞ax2+x-2.

當a＜0,x≥3 時，ex＞x2，

所以f(x) ＞(x-2)x2+a(x-1)2＞(x-2)x2+ax2=x2(x-2-a).

取x2=max{3,2-a}∈(1,+∞)，則f(x2)＞0.

例4（源自2017 年新課標全國Ⅰ卷理第21 題）已知0 ＜a＜1，函數f(x)=ae2x+(a-2)ex-x.

證明：存在x1∈(-∞,-lna)，f(x1)＞0；存在，x2∈(-lna,+∞),f(x2)＞0.

則f(x2)＞ex2-x2＞0.

例5（源自2018 年新課標全國Ⅱ卷理第21 題）已知函數證明存在x0∈(2,∞)，f(x0)＞0.

分析與探究當x≥5 時，

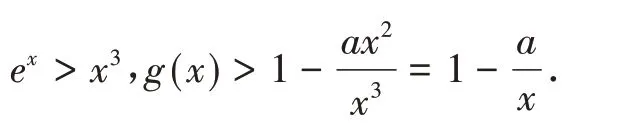
取x0=max{5,a}∈(2,+∞)，則g(x0)＞0

例6（源自2021 年高考全國甲卷理第21 題）已知a＞1，函數g(x)=a·lnx-lna·x.證 明：存 在，g(x0)＜0.

分析與探究因為lna·x關于x是一次的，所以要將a·lnx放大為關于x的次數小于1 的冪函數，以確保lna·x仍起主要作用.

二、函數極值點的偏移問題

例7（2021 年新高考全國Ⅰ卷第22 題）已知函數.

（1）討論f(x)的單調性；

（2）設a，b為兩個不相等的正數，且blna-alnb=a-b，證明：

分析與探究第（1）題是容易題，f(x)的增區間是(0,1)，減區間是(1,+∞).第（2）題是難題，難點一是條件等式變形，難點二是不等式的證明.

將條件等式兩邊同除ab，并移項得

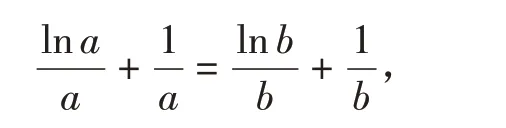
結合f(x)的表達式，可進一步化為

左邊不等式的證明，在往年的高考題中多次出現，被稱為“極值點偏移”問題，一般用構造函數法證明.如2010 年天津卷理第21 題、2016 年新課標全國I卷理第21 題.

對于右邊的不等式，如果也用證明左邊不等式的方法，可有如下思路：

由第（1）題知，f(x)在(0,1)內遞增，在(1,+∞)內遞 減，f(e)=0，不妨設0 ＜x1＜1 ＜x2＜e，則x2,ex1∈(1,+∞).

x1+x2＜e?x2＜3-x1?f(x2)＞(e-x1)?f(x1)＞f(e-x1).

設F(x)=f(x)-f(e-x)，0 ＜x＜1，只要證明F(x) ＞0.

由F′(x)=-ln[x(e-x)]=0，得

易知f(x)在(0,α)內遞增，在(α,1)內遞減.

因為f(x)在(1,+∞)內遞減，

所以F(1)=f(1)-f(e-1) ＞0.

但因F(x)在x=0 處沒有意義，在高中階段無法嚴謹說明當x∈(0,α)時，F(x) ＞0.

如下證法很好地避開了函數在x=0 處的值.

由0 ＜x1＜1，得1-lnx1，x1(1-lnx1)＞x1，即f(x1)＞x1?f(x2)＞x1.

所以x1+x2＜x2+f(x2)=2x2-x2lnx2.

設h(x)=2x-xlnx，1 ＜x＜e.

則h′(x)=1-lnx＞0，h(x)在(1,e)內遞增.

所以h(x2)＜h(e)=3，這就證明了x1+x2＜e.

如果教師將這樣的證法講給學生，學生只會感嘆太精彩、太巧妙，但想不到、記不住，下次遇見仍然不會，更別說舉一反三了.要避免只給學生講解法，而要讓學生體會并明白解法的背景和構思的理由.

下面從函數圖象上對x1+x2給出一個直觀的解釋.

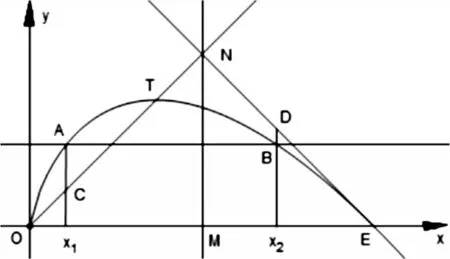
圖1

設T 為圖象的頂點，MN 為線段OE 的中垂線，作直線OT、直線OT 關于直線MN 對稱的直線EN.直線ON 的方程是y=x，直線EN 的方程是y=-x+e.從圖中可以看出，

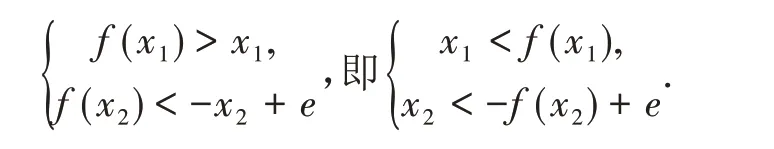
因為f(x1)=f(x20，將以上兩式相加即得

x1+x2=e.

這就很自然地引導學生去證明f(x1)＞x1和f(x2)+x2＜e.

綜上，文章通過新高考全國數學卷函數零點個數及極值點偏移問題的分析與探究，提出了先將超越函數放縮成冪函數及“以直代曲”構造函數的思路，并通過近年全國高考試題的類比，找到了解答此類問題的通性通法，優勢是做一題得一法會一類的目的，避免“題海戰術”.