淺談培養學生幾何直觀能力的策略

馮建青

【摘 要】數學學習的知識點既有“數的特征”，又有“形的特點”。高年級學生對數學產生畏難情緒，是因為解題時無法像低年級時期對題目產生直接判斷。這種對題目直接判斷的能力是不經過邏輯分析的，需要學生具有直觀能力，直觀能力的養成不是一蹴而就的，需要在各年級的學習中重點

培養。

【關鍵詞】數學學習 幾何直觀能力 培養策略

關于幾何直觀，在《義務教育數學課程標準（2011年版）》中強調的是利用圖形描述和分析問題，具體內容如下：借助幾何直觀可以把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路，預測結果。幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要的作用。筆者認為，幾何直觀能力強的學生可以對題目產生直接預判，這種直接判斷的能力是不經過邏輯分析的，而幾何直觀能力是一種經驗的積累，應在各年級中重點培養。本文基于筆者的課堂經驗，闡述了在小學各年級的數學學習中培養學生幾何直觀能力的重要性，以及培養幾何直觀能力的策略。

二、以形助教，發展低年級學生識圖能力

數學學習是學生思維從直觀走向抽象的過程，學生在低年級時應該牢牢打下把數學信息符號化、抽象化的基礎。在低年級的教學過程中，教師應著重培養學生觀察圖片的能力。

1.用數學的眼光觀察圖片

低年級學生在觀察圖片時隨意性大，識圖時沒有重點和方向，隨著自己的興趣來看圖，得出的看圖結果往往是片面的，容易遺漏重要的數學信息。例如，蘇教版數學二年級上冊第三單元《表內乘法》第1課時，學生在看教材中的相關圖時能直接看出有雞和兔兩種動物，要是問學生“兔有多少只”“雞有多少只”學生往往會用已有經驗一只一只地數，如此就沒有達到教學目的了。

教師應先讓學生充分觀察圖片，在學生第一次觀察圖片得到圖中“有2種小動物”的前提下，還要深入識圖得到“小雞3只一堆”“小兔2只一堆”的結果，讓學生在圖中對應位置標記上“3只雞”“2只兔”，滲透圖片表達的“幾個幾”的含義，讓學生能夠列出算式：

雞：3+3+3+3=12（只）。

兔：2+2+2=6（只）。

學生在總結學習過程時，不僅是根據算式說出有“4個3、3個2”，而且有圖片作為依托。學生通過看一看、標一標，才能有效地理解圖片表達的信息，在以后識圖時，能夠用數學的眼光、數學的思維觀察圖片。

2.用圖畫代替實物演示

愛動、愛玩是學生的天性，低年級學生注意力持續時間短，在低年級課堂上教師經常會借助實物演示、準備教具學具，讓學生在實踐中獲得數學知識、在操作中發展數學思維。這樣將理論和操作相結合是以學生為主體的教學，是新課程標準所提倡的以人為本的課堂。然而許多課堂教學中，教具繁復難以在日常課堂中準備，需要學生擁有幾何直觀能力，對圖片進行簡單的加工。例如，蘇教版數學二年級上冊第四單元《表內除法》第1課時，除了課件演示如何將8個桃子每2個一份平均分，讓學生理解平均分的概念，還要讓學生動手在圖上每2個桃圈一份，一共圈出了4份，就是可以分給4個小朋友。

用圖畫代替實物，從具體的實物演繹到抽象的幾何標記，是學生思維能夠達到的水平，也是發展幾何直觀能力的重要契機。教師只有重視在低年級時培養學生的識圖能力，學生才能發展相應的幾何直觀能力，為中高年級將復雜的題目簡單化、將抽象的知識形象化打下堅實的基礎。

三、以數解形，發展中年級學生畫圖能力

在計算時，如果數字大、方法復雜，我們要提倡學生用豎式計算。那么在數量關系越來越復雜、接受的數學知識在生活中不常見時，我們也可以要求學生用畫圖的方法來梳理數量關系，借助簡明、形象的幾何圖，延伸解題思路，促進學生邏輯思維能力的提升。

1.從簡單開始，實現數向形轉化

小學生處在形象思維為主的階段，強迫學生掌握抽象的知識體系，只能讓學生對數學學習敬而遠之，無法讓學生真正成為學習的主人。利用圖形幾何解析題目，能把復雜的題目簡單化、把抽象的題目形象化。不同類型的題目可以畫不同的幾何圖形，比如線段圖、立體圖、示意圖、路程圖、思維導圖。但是不能為了畫圖而畫圖，要讓學生用圖畫、符號來表達自己的意思，比如，蘇教版數學五年級上冊第一單元《負數的初步認識》中，抽象的負數概念不如正數概念清晰，學生生活中接觸得比較少。在建立負數的概念時，教師可以讓學生畫一畫電梯中的樓層示意圖，地面為0，地上就是用正數表示、地下就是用負數表示。而把這個示意圖放平，那就是數學家所說的數軸了。

學生利用有限的生活經驗，畫出了電梯樓層的示意圖，再在示意圖的基礎上加以演繹推理得到了正數和負數的概念。這項概念是在學生已有的知識基礎上演繹得來的，學生容易接受也容易理解透徹。用幾何圖形來幫助理解題目，能把抽象的知識躍然紙上，讓人一目了然，實現數向形的轉化。

2.向復雜過渡，透析數量關系

中年級的數學題目中的量未必龐大，但是數量之間的關系開始復雜化了。這種復雜就像是計算數字較大的乘除法時要用豎式計算，對于較為復雜的數量關系，我們則需要利用線段圖來解析，在用線段圖來表示時應做到以下兩點：

（1）在用線段圖時要讓學生厘清線段圖之間的關系，也就是看圖說話、厘清題意。

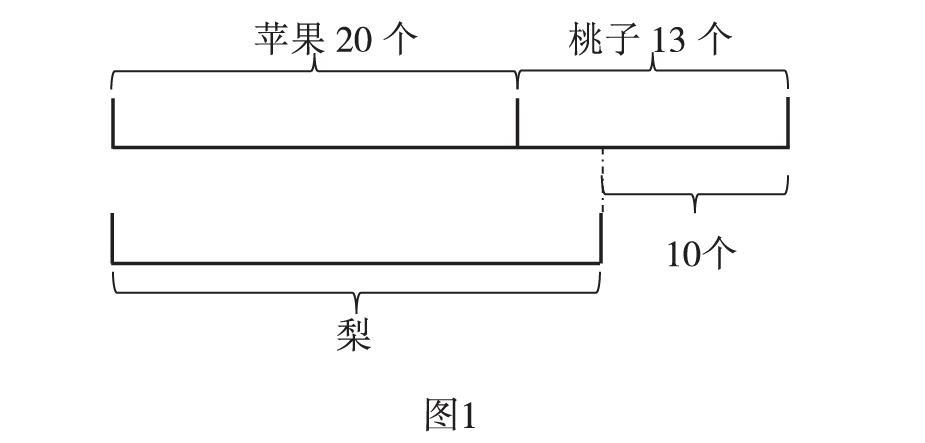
像圖1這樣關系稍復雜的線段圖，要讓學生先看懂圖，知道“蘋果有20個，桃子有13個”，還要能說出數量之間的關系“梨比蘋果和桃子的總數少10個”。在線段圖中看懂了關鍵的數量關系之后，再提出問題。有的學生提出問題“梨有多少個”，根據圖意解題可以拓寬學生的解題思路。線段圖等幾何圖可以幫助學生梳理數量之間的關系，對結果產生預判，是學生應掌握的解題技巧。

（2）教師要加強中年級學生對于線段圖的比較，能在不同的線段圖中找到相同點。

數學是抽象的，數學知識點既有“數的特征”，又有“形的特點”，教師要用幾何圖在直觀與抽象之間架起橋梁。例如，當問題“兩堆煤共有1440噸，第一堆煤比第二堆多120噸，問兩堆煤原來各有多少噸”和“兩堆煤共有1440噸，如果從第一堆運送120噸到第二堆，那么兩堆煤的噸數一樣多，問兩堆煤原來各有多少噸”一起出現時，學生總是厘不清思路，不知道這兩題的區別。這時需要用線段圖來解析，把復雜的數量關系先梳理清楚。第一個問題中，第一堆煤多，比第二堆多120噸;第二個問題中，第一堆煤多，多了兩個120噸。第二個問題中“多了兩個120噸”比較抽象，需要借助畫線段圖的方法幫助學生分析題意、增強析圖能力。

在中高年級中，由于數量關系的復雜化，學生對題目進行預判越來越難，借助幾何圖形剖析題意，是學生必須掌握的數學技巧。在中年級應加強學生的畫圖能力，簡單的題目學生能在腦海中直接列出幾何圖，復雜的題目能落于紙上，再抽絲剝繭進行解答。

四、數形互助，發展高年級學生析圖能力

“數缺形時少直覺，形少數時難入微。”代數知識容易計算，但缺乏形象性;幾何知識具體且形象，能夠便于理解。

1.用幾何圖梳理思路，在幾何圖中明確數量關系

蘇教版數學五年級上冊便開啟了代數的新領域，許多教師發現學生難以掌握這個單元的知識點。這論證了代數的抽象性，學生應結合幾何圖的形象性，從而將代數向幾何轉化。從幾何中抽取數量關系，靈活地將代數與幾何互相轉換能加深學生對題目的理解。高年級學生能依托幾何，靈活進行數形結合，在低中年級識圖、畫圖的基礎上水到渠成的養成析圖能力。

例如，在蘇教版數學六年級上冊第五單元《分數四則運算》中，有問題“六年級一班有48人，其中2— 3喜歡跳舞，3— 4喜歡唱歌，沒有人既不喜歡跳舞又不喜歡唱歌。既喜歡跳舞又喜歡唱歌的有多少人？”題中總人數已知，學生要學會從分數的角度出發找到分數的“單位1”，喜歡跳舞的人占了全班的2— 3，喜歡唱歌的人占了全班的3— 4。根據這一理解，喜歡唱歌和跳舞的分數“單位1”都是全班人數，即把全班人數看作“1”。于是可以將代數向線段圖轉換，全班可以分為喜歡跳舞的人和喜歡唱歌的人，但是有一部分重合了，這部分便是題目中所求的“既喜歡跳舞又喜歡唱歌的人”。對線段圖再次進行分析，如果把喜歡跳舞和唱歌的人都合起來，總人數是大于全班人數的，得出第二個線段圖。利用線段圖可以清晰地看出關系式，2— 3+3— 4>1，多出的部分便是“既喜歡跳舞又喜歡唱歌的人數”。（詳見圖2）

2.借助幾何圖形理解，用幾何圖形記憶概念

在蘇教版數學五年級上冊第八單元的綜合活動課程中，學生通過觀察、猜測、實驗、分析和得出結論，積累寶貴的研究經驗。最后在得出結論時，能從語言表達向字母表達轉換，賦予字母意義。字母便作為一種概念，印在了學生的腦海中。

像這樣根據題目畫出幾何草圖，再根據幾何圖剖析數量關系式，是高年級常用的解題技巧，也是為學生將來學習更抽象的代數知識打下基礎。學生通過識圖、畫圖、析圖，能充分理解問題、發現問題的本質，展開直觀思維的羽翼。有了良好的幾何直觀思維能力，學生在將來的學習中一定能夠有目標、有順序地思考問題。

數學學科毫無疑問是一門抽象的學科。學生從入學開始便在學習把知識符號化，將形象的事物抽象化。幾何直觀能力是學生數學學習必備的數學能力和解題技巧。在提倡學生為主體的課堂教學中，教師要把幾何直觀能力滲透在日常的數學教學中，把培養學生的幾何直觀能力作為一種課堂意識，在小學各階段加以培養。