分塊矩陣在矩陣秩理論教學中的探討

唐大釗，李 丹

（1.重慶師范大學數學科學學院，重慶 401331；2.重慶市大學城第一中學，重慶 401331）

分塊矩陣不僅是高等代數課程中的重要內容，而且也是相關后續課程中研究問題的重要工具。作為反映矩陣固有特性的重要指標——矩陣秩，它不僅是向量組秩橫向和縱向的推廣，而且是構成矩陣理論的基石。因而，矩陣秩之間的關系（等式關系、不等式關系）的證明及推導就顯得非常重要。然而，有關矩陣秩的等式和不等式不勝枚舉，如何以一種較為有效的方式統一地去處理這類問題是每一個高等代數授課老師需要思考的問題。

矩陣的分塊是處理矩陣一種有效方法，它能使階數較高矩陣的計算變得簡潔和快速，容易被學生接受和理解。此外，矩陣的分塊這一處理方式能進一步開拓學生思維，對于提高學生靈活解決問題的能力，進而培養學生的創新思維能力都有積極作用。基于筆者近年來對于高等代數和線性代數課程的教學經驗，本文將主要探討分塊在矩陣秩理論中的應用，包括利用矩陣的分塊證明矩陣中的若干重要定理，以及涉及矩陣秩的若干不等式。從實際效果看，這些探討增強了學生對于高等代數矩陣秩理論章節的理解，相當程度上改善了教學效果。

1 矩陣的秩、矩陣的分塊及其相關運算

在本節中，我們主要回顧矩陣的秩和矩陣的分塊。

定理1.1[1]矩陣的行秩（列秩）指矩陣的行（列）向量組的秩。因為矩陣的行秩等于列秩，因而將其統稱為矩陣的秩，記為。

定義1.1[2]初等矩陣是將單位矩陣進行一次初等變換得到的矩陣。

定理1.2[4]矩陣的初等變換不改變其秩。

接下來，我們回顧在處理階數較高的矩陣時一個重要的工具——分塊矩陣。將某些給定的大矩陣看成若干小矩陣組成，就如同將矩陣看成由一個個數組成一樣。在矩陣的相關運算中，將這些特定劃分好的小矩陣當成數一樣來處理，這一處理方式就是所謂矩陣的分塊。唯恐言之無物，我們試舉下面的例子來加以說明。矩陣

這就是我們所說的矩陣的分塊。

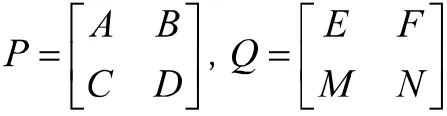
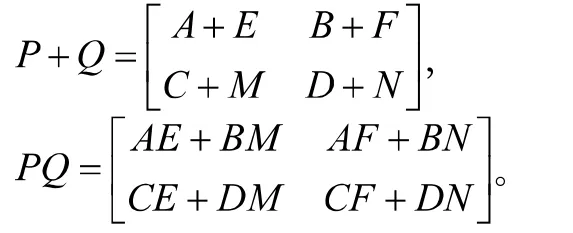
2 分塊矩陣在矩陣秩相關定理中的應用

在本節中，我們將探討利用分塊矩陣對矩陣秩相關定理的證明。

3 分塊矩陣在矩陣秩不等式關系的應用

分塊矩陣不但為討論抽象矩陣和抽象矩陣的秩構造了一架橋梁，而且分塊矩陣與矩陣的初等變換是緊密聯系的，利用矩陣的分塊，可以對一些抽象矩陣的秩進行更深一步的討論。在本節中，我們給出三個例子，探討分塊矩陣在矩陣秩中的應用。

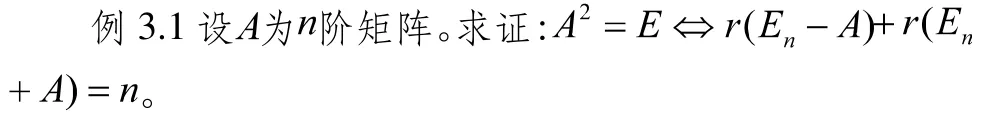
分析：雖然上述條件是以行列式的形式給出的，但是題設中也不乏矩陣的秩之間的關系，而且行列式與其所對應的矩陣之間具有非常緊密的聯系，這自然而然想到利用分塊矩陣。

4 總結

一方面，分塊矩陣對于行列式的計算和證明有著非常巧妙的應用，這主要體現在簡化行列式的計算上。分塊矩陣可以將一些高階行列式通過分塊以及其他的一些初等變換，簡化為求一些較為低階行列式的問題，由于行列式與其對應矩陣的秩之間有著非常密切的聯系，因而分塊矩陣是計算和證明行列式等式或不等式的一個有力的工具。

另一方面，在證明矩陣秩相關不等式的過程中，分塊矩陣仍有不可忽視的作用，因為分塊矩陣將具體的矩陣抽象為一些“小”矩陣塊，這就在處理問題的時候提供了許多簡捷的技巧；分塊矩陣對處理矩陣的秩方面尤其便利，它將一些抽象矩陣，通過初等變換轉化為一些基礎矩陣（如單位矩陣、可逆矩陣等）的問題，這使得問題在一定程度上獲得簡化。不僅如此，分塊矩陣對于研究矩陣的性質（如逆矩陣、矩陣的特征值、Jordan標準型等）也有著非常重要的應用。

綜上所述，分塊矩陣在處理涉及矩陣秩的相關不等式時，體現出了強大的統一處理能力。然而，學生需要就具體問題熟練地挑選或者構造出相關的初等矩陣，這就需要平時多對相關習題中分塊矩陣的選取進行觀察、歸納和總結。另一方面，教師在講授完分塊矩陣這一工具后，也應該幫助或者引導學生對其進行系統歸納和總結。總之，筆者認為，為了使學生更好理解高等代數這門課程，教師應當根據教學大綱和授課對象，選取最優的教學內容和合理的教學方案。在教學過程中，可以及時對所學知識進行系統歸納并進行相關應用，使學生真正體會到高等代數這門課程的真正魅力所在，提高其學習積極性，實現最佳的教學效果。