指向數學思維提升的問題設計

福建省上杭二中 (364200) 黃財英

問題是驅動學生思維活動的向導，是學生課堂深度學習的助推器，能有效激發學生的求知欲、探索欲、表現欲、創新欲.通過問題設計，可以把知識的邏輯結構與學生的思維過程有機的聯系起來，使知識的邏輯結構轉化為學生的認知結構，讓學生發現數學的內在規律，認識理解數學本質.教師若能重視學生認知的“最近發展區”計有效的問題，將會大大提高課堂教學質量.

1.懸念問題，開啟思維

“良好的開端是成功的一半”,講授新課之前，先設置懸念問題，可以觸發學生的求知動機，產生一種非知不可的緊迫心情.此時，學生的注意力高度集中，思維處于積極的狀態，教師最容易吊起學生的學習興趣.

例1 拋物線概念的教學

講授拋物線的概念，可預設懸念，誘發好奇心理，引發探究欲望，激發學習熱情，開啟思維，設置以下問題：

(1)橢圓與雙曲線都有兩個焦點、兩條準線，你們見過只有一個焦點與一條準線的曲線嗎？(懸念1：提出單焦點、單準線曲線的存在性，誘發好奇心理)

(2)橢圓與雙曲線的離心率的取值范圍分別是01的常數，那么有沒有離心率e=1的曲線呢? (懸念2：引發探究欲望)

(3)其實在初中我們已對這類曲線做了簡單的研究，你們能猜出是什么曲線嗎? (懸念3：學生非常驚訝，真的在初中就研究過了嗎?那是什么曲線呢?引起學生質疑，思考)

通過以上預設問題，學生基本上會猜想到這是拋物線，接下來可繼續設置以下問題：

(4)由橢圓與雙曲線的第二定義：對平面內的一個動點，若它到一個定點與到一條定直線(定點不在定直線上)的距離之比是一個常數e，當01時，動點的軌跡是雙曲線；那么e=1時，動點的軌跡是拋物線嗎?(懸念4：引起學生類比、聯想、探究)

(5)橢圓與雙曲線的標準方程都分別有兩個，那么拋物線的標準方程會有幾個呢?(懸念5 ：為推出拋物線的四個標準方程埋下伏筆)

一連串層層深入的問題使課堂教學跌宕起伏、妙趣橫生，幾乎使學生忘記是在上數學課，而是在做一項動人心魄的思維游戲，學生的學習主動性、積極性得到充分的發揮，學生在疑問、思考、探索、解決問題中得到概念的理解、知識的融會、方法的滲透、能力的提升，在這種氛圍之下還用憂愁課堂教學中學生思維不開啟嗎？所以說，教學方法一旦觸及學生的情感和意志領域，觸及學生的心理需要，這種教學就變得高度有效.

2.變式問題,激活思維

數學就其本質而言是一種思維，數學課堂的根本就是培養和發展學生的數學思維能力.通過變式問題教學，力求做到思維遷移具有深刻性、發展性和創造性，變式訓練具有拓展性、探索性和靈活性.教師由淺人深，循序漸進，多層次、多角度、多觀點、多變化地設計了如下的變式問題教學，通過問題的變化、引申，培養和提高學生思考、解決問題的能力.

例2 (1)若方程x2-(m+1)x+4=0有兩個不等實數根，求實數m的取值范圍;

(2)若方程x2-(m+1)x+4=0在[0,3]上有兩個不等實數根，求實數m的取值范圍;

(5)已知拋物線y=-x2+mx-1,點M(0,3)，N(3,0)，若拋物線與線段MN有兩個不同的交點，求實數m的取值范圍;

(6)若不等式x2-(m+1)x+4>0在[0,3]上恒成立，求實數m的取值范圍.

以上問題有基本、有變式、有拓展、有延伸，形成了一個問題串，構成了思維的整體性，體現了思維的層次性和探究性.在問題串的引領下，學生進行系列的、連續的思維活動，不斷攀升思維的新高度，強調了解題策略的成因分析，不僅有利于學生思維的飛躍，加深對數學本質的認識，同時，通過經歷問題的形成和解決過程，激活學生思維，能有效提高學生提出問題、分析問題和解決問題的能力.

3.錯誤問題,批判思維

教學過程應強調師生互動，學會從學生的角度思考問題，與學生共同交流解題思路，及時發現學生中的典型錯誤問題，教師也應在課堂上適時地進行“誘錯”、“示錯”，然后引導學生進行“辯錯”、“識錯”、“明錯”、“改錯”，讓學生從“錯誤”走向“正確”.從一定意義上講，“錯誤”比“正確”更有教學價值，教師應深深地意識到“錯誤”與“正確”都是教學上的重要資源.

此題若直接講解，簡單明了，節省時間.但筆者以“錯誤與正確都是教學上的重要資源”為指導，先讓學生練習，再交流，最后完成解題.

學生出現的主要兩種典型錯誤問題如下：

以上不僅正確解答了題目，而且分析了解題中的常見錯誤，錯中求正，敗中求勝，有效防止類似錯誤的再次發生，提高解題正確率.

4.多解問題,優化思維

教學過程中，如果不時對一些問題提醒學生進行解題后的反思，可以有效地幫助學生加深對概念的認識和理解，有效地克服解題思路的偏差和不透徹，優化解題過程，對自己的解題方法的優劣加以評價，尋找最佳方案，從而培養他們嚴謹的學習態度，提高學生的分析綜合能力.

這是一道具有很高訓練價值，對提高同學們分析問題、解決問題的能力有很大的作用，是培養思維的全面性、深刻性、批判性、靈活性的良好素材，師生提供以下解法并展開反思.

解法1：設t=cosαsinβ，則

∵-1≤sin(α+β)≤1且-1≤sin(α-β)≤1，

反思1：這是被普遍認為正確的解法.但師生分析后同時也認為以上解法有不足之處.為什么取以上兩者的交集就是正確答案了呢？它是充要條件了嗎？

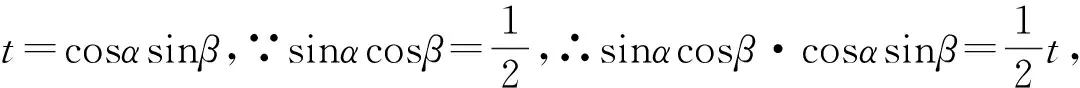
反思3：通過反復分析，師生認為這是一種相對條理清楚、邏輯嚴密、科學有效的解法.

5.規律問題,總結思維

數學學習離不開解題，但不能陷入題海，不能讓學生成為解題的機器.對做過的題目要進行反思總結，并站在一定的高度加以審視，從中發掘題目的精髓，看清問題的本質，對數學有思有悟，這樣，學生才能從更高的觀點，用更寬的視野，更理性的眼光，去思考解決數學問題，讓數學問題不斷規律化，讓數學課堂不斷出新出奇出彩.

例5 (1)10個同樣的小球，隨機放入3個盒內，求有多少種不同的方法；

(2) 求方程x1+x2+x3+x4=9的非負整數解的組數；

(3) 試問(x+y+z)12有多少項？

(4) 用7種不同顏色的1種，或2種，或3種，或4種，分別涂在正四面體各個面上，一個面不能用兩色，也無一個面不著色，問共有幾種著色法？

“問題是數學教學的心臟.”因心臟的搏動，思維才如同血液般運動，整個課堂才變得靈動高效.教學中要有意識地以數學問題之石激起師生思維之浪，讓數學課堂教學高潮一浪高過一浪.