拋物線中雙定點性質(zhì)的探究*

江西省南昌市第一中學 (330000) 喻瑞明

拋物線性質(zhì)的教學是高中數(shù)學教學實踐中不可缺少的一部分，有關拋物線性質(zhì)的考題也是層出不窮.我們知道，拋物線中蘊含了許多優(yōu)美的結(jié)論，本文從2018年全國Ⅰ卷文科第20題考查拋物線的性質(zhì)出發(fā)，利用幾何畫板探究了拋物線中雙定點的一些性質(zhì)，供同仁參考.

文[1]中已探究了拋物線的性質(zhì)，并得到如下結(jié)論：

結(jié)論1 如圖1，已知拋物線y2=2px(p>0)，點B(-m,0)(m>0)，設斜率存在的直線l與拋物線相交于M,N兩點，則直線l過定點A(m,0)的充要條件是kBM+kBN=0.

結(jié)論2 如圖2，已知拋物線y2=2px(p>0)，A(m,0)，B(-m,n)(m≠0)，直線l過點A且與拋物線相交于P,Q兩點，則kPB+kQB=2kAB.

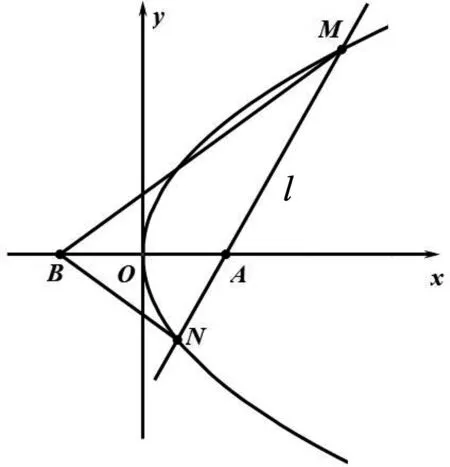
圖1

圖2

綜觀上述兩個結(jié)論，我們可以發(fā)現(xiàn)，得出了已知兩個定點A,B的拋物線的兩條性質(zhì)，本文依此為背景，進一步研究的拋物線中雙定點的一些性質(zhì).

首先，我們先一起探究以下引理：

引理若A(x1,y1),B(x2,y2)是拋物線C:y2=2px(p>0)上不相同的兩個點，則直線AB的方程為(y1+y2)y=2px+y1y2.

以此引理為基礎，以幾何畫板為手段，探究得出如下結(jié)論：

圖3

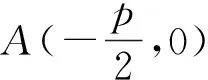
圖4

由結(jié)論3，進一步探究得出結(jié)論4.

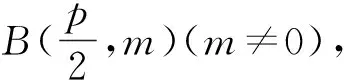
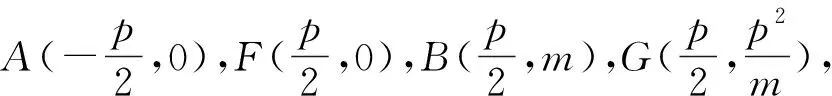
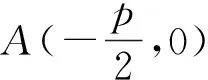
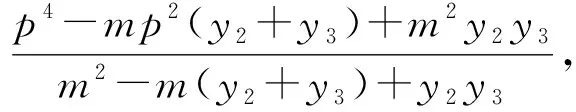
由結(jié)論3、4，進一步推廣得出結(jié)論5和結(jié)論6.

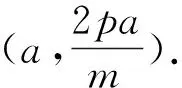
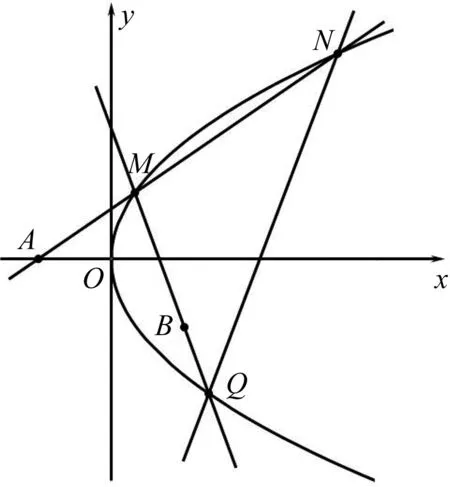
圖5

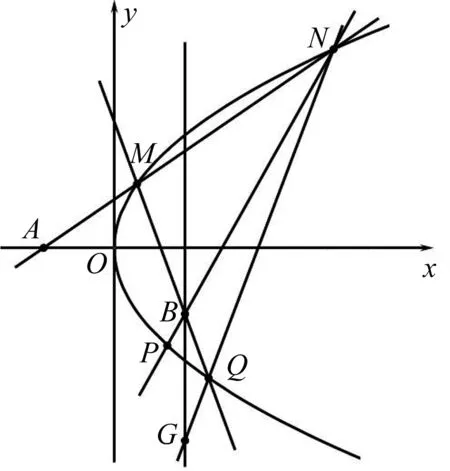
圖6

結(jié)論6 如圖6，已知拋物線C:y2=2px(p>0)，定點A(-a,0)(a>0)，定點B(a,m)(m≠0)不在拋物線C上，過點A的直線與拋物線C相交于M,N兩點，直線MB與拋物線C相交的另一個交點為Q，記直線NQ恒過的定點為G，直線NB與拋物線的另一個交點為P，則(1)A,P,Q三點共線；(2)M,P,G三點共線.