橫風作用下列車抖振力氣動導納風洞試驗研究

張鵬，樊紹文，許洪剛，敬海泉,3

(1.國家鐵路局 安全技術中心，北京 100160；2.中南大學 土木工程學院，湖南 長沙 410075；3.高速鐵路建造技術國家工程實驗室，湖南 長沙 410075)

下承式鋼桁梁以其突出的優點，在高速鐵路大跨度橋梁中的運用越來越普遍，特別是對于公鐵兩用橋梁，由于桁架腹桿的遮擋作用，行駛于桁架內的列車在橫風作用下與主梁之間的氣動干擾較大，現有列車氣動導納識別結果可能并不適用，目前國內針對于下承式鋼桁梁內列車氣動導納的相應研究還相對較少。為保障列車運營安全，大量學者對橫風作用下的車橋系統進行了分析研究。鄒云峰等[1-4]采用車-橋氣動力同步分離裝置和列車、橋梁節段模型，在不破壞車橋間的氣動干擾的條件下，對列車和橋梁所受到的靜風氣動力進行風洞試驗測試，分析了風攻角、車橋組合方式、橋梁結構形式等因素對車橋氣動力的影響規律。COOPER 等[5-6]在大量風洞試驗和實車試驗數據的基礎上，結合矩形截面氣動導納函數的定義，推導出列車側向力氣動導納理論公式。段青松等[7]基于數值模擬的方法，驗證了平板升力氣動導納模擬結果的可靠性，并對單獨列車截面的升力氣動導納及繞流特性進行分析。研究結果表明：平板升力氣動導納數值結果與解析解吻合較好，數值識別方法可靠。張志田等[8]采用Küssner 類型函數對抖振力以及氣動導納在時域內進行模擬，對某大跨度懸索橋初步設計方案進行了風洞試驗,得到該橋梁加勁梁斷面的氣動導納。分析結果表明采用Küssner 函數法可靈活地將頻域內的氣動導納轉換為時域函數，從而便于考慮各類非線性后進行動力有限元分析。目前對列車氣動導納的識別方法主要采用等效導納法，即假設脈動風水平分量和豎向分量對抖振力導納函數的貢獻作用相同，而事實上不同脈動風速分量對結構抖振力的作用大小是不同的，因此不同脈動風分量相應的氣動導納函數也應是不相同的，同時該種氣動導納識別方法不適用于多模態耦合的抖振分析。本文以一座典型大跨度下承式四線鋼桁斜拉橋為研究背景，在車橋耦合測力測壓風洞試驗系統的基礎上，采用自譜-交叉譜綜合最小二乘法列車氣動導納進行識別，研究車橋不同組合方式和紊流特征參數對列車氣動力和氣動導納的影響。

1 氣動導納理論及識別方法概述

目前抖振在頻域分析的方法中，大多按照Davenport 準定常理論進行計算，然后引入氣動導納函數對脈動風速沿橋梁構件截面方向的不完全相關性和非定常特性進行修正。其抖振力譜表述如下：

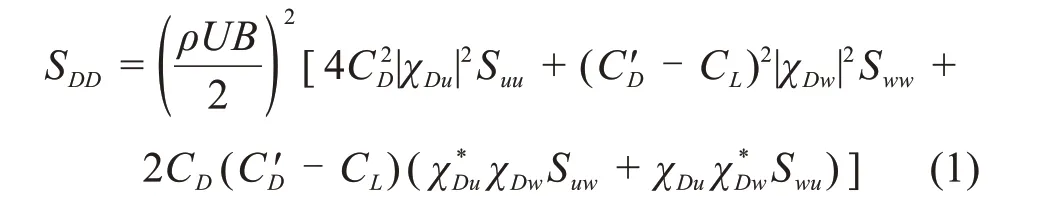
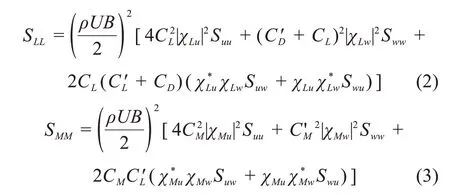
式 中：χDu，χDw，χLu，χLw，χMu，χMw為氣動導納函數。

忽略式(1)～(3)中脈動風速互譜函數，抖振力譜表達式可簡化為：

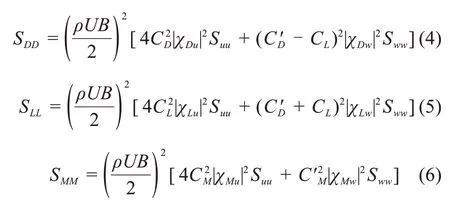
可以看出氣動導納函數是由脈動風譜到抖振力譜的傳遞函數，WILLIAM[11]基于勢流理論推導了機翼斷面的理論氣動導納函數：

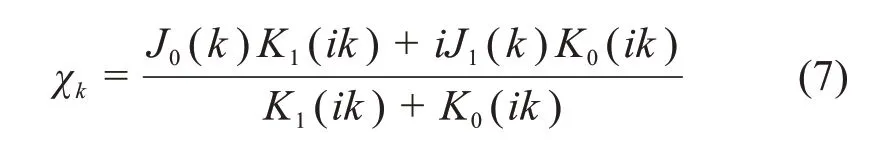
式中：k為機翼斷面弦長和紊流波長的比值；i為復數的虛部單位；f為工程頻率，Hz；J0，J1為第1類Bessel函數；K0，K1為修正的第2類Bessel函數。

隨后，LIEPMANN[15]提出了Sears 函數模的簡化表達式：

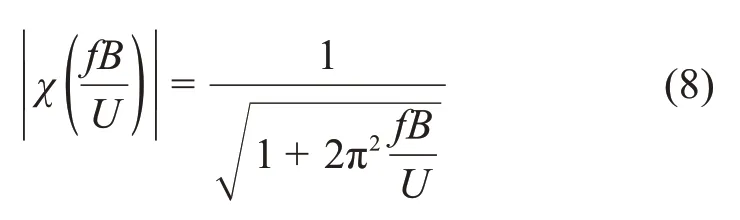
Sears 函數是基于勢流理論的推導結果，即具有流線幾何外形的機翼在升力作用下的氣動導納，而工程結構中大多是鈍體截面，來流在結構表面會出現嚴重的分離、再附現象，因此，直接將Sears 函數用于鈍體結構截面的氣動導納必然將產生較大的偏差。鈍體斷面氣動導納函數的求解至今沒有成熟的理論方法，一般通過試驗進行識別，主要有系統識別法和直接測量法。

系統識別法通過測量結構模型在脈動風作用下的振動響應和試驗風場的紊流特性，根據推導出的脈動風到結構模型振動響應之間的傳遞函數矩陣來得到氣動導納函數，該種方法屬于間接測量，系統的不確定因素和干擾會降低氣動導納識別的精度，因此受系統較大的制約。基于測力試驗的直接測量法是應用最為廣泛的氣動導納識別方法，其基本思路是利用測得的抖振力時程數據和脈動風速時程數據，根據抖振力的頻域表達式求解得到氣動導納函數。目前氣動導納直接測量法的主要方法有等效氣動導納法、交叉譜法、零點分離法、分離頻率識別法和自譜-交叉譜總體最小二乘法。

相較而言，自譜-交叉譜總體最小二乘法優越性最大，綜合了等效導納法和交叉譜法，既能全面地傳遞紊流場和抖振力之間的脈動信息，又可很方便地分離出6個氣動導納，可以進一步分析研究不同脈動風分量對結構振動響應的貢獻，因此本文將采用該種方法識別列車氣動導納。

在對列車氣動導納的識別過程中，需要多次運用最小二乘法求解，傳統的尋優算法一般需要給定初始值，同時容易陷入局部最優解，降低了識別精度。本文采用遺傳算法進行求解，從問題解的串集開始搜索，而不是從單個解開始，覆蓋面大，有利于全局尋優。遺傳算法的參數設置如表1所示。

表1 遺傳算法參數設置Table 1 Setting parameters of genetic algorithm

以0°攻角、B類格柵紊流場下，單列車位于第2 車道位置時為例，B 測壓截面的氣動導納單次求解最小二乘殘量隨遺傳代數的變化如圖1所示，殘量值隨遺傳代數的增加快速衰減，當遺傳代數超過50次時基本趨于穩定，說明已得到最優解。

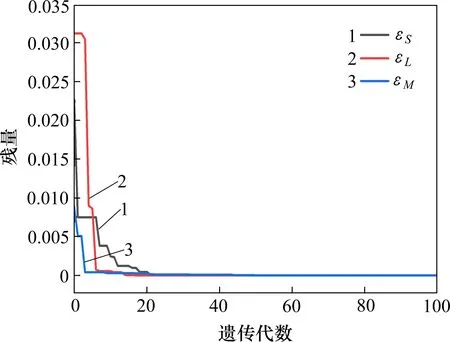
圖1 最小二乘殘量變化圖Fig.1 Residual change diagram of least square

2 試驗概況及參數設置

2.1 試驗概況

以一座典型大跨度下承式四線鋼桁斜拉橋為研究背景，主梁節段模型采用1/40的幾何縮尺比，模型長2.0 m，寬0.608 m，高0.35 m，長寬比3.29。列車縮尺比例為1:40，長2.0 m，寬0.075 m，高0.875 m。本文研究所涉及的風洞試驗均在中南大學風洞實驗室高速試驗段中進行，該風洞為閉口回流低速風洞，洞體為全鋼結構。風洞洞體由動力段、試驗段、拐角段(導流片)、收縮段和蜂窩器等部分組成。該風洞具有2個試驗段，其中低速試驗段尺寸為18 m×12 m×3.5 m(長×寬×高)，風速范圍0～20 m/s，紊流度小于1%；高速試驗段尺寸為15 m×3 m×3 m(長×寬×高)，最高風速0～94 m/s，紊流度小于0.5%。該風洞具有試驗段尺寸大，設計風速高，流場品質好等特點。

為便于試驗描述，在風洞試驗室高速試驗段中定義一個風洞坐標系，如圖2 所示，x方向為風洞來流方向，z方向為垂直風洞底面向上，按照右法則確定水平y向，原點O為風洞底面和風洞高速試驗段起始截面交線的中點。風洞坐標系中x，y，z方向與眼鏡蛇探頭所約定的風速方向u，v，w一致。

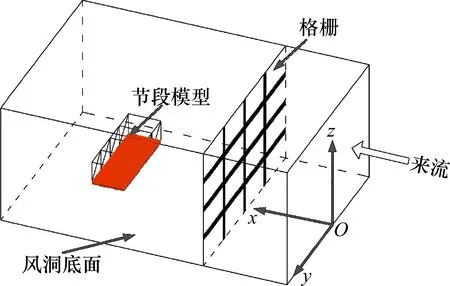
圖2 風洞坐標示意圖Fig.2 Schematic diagram of wind tunnel coordinates

2.2 紊流場格柵布置

格柵紊流場所用格柵由高強度木板搭接而成，木板間用U 型夾連接固定。為滿足試驗要求，通過調整格柵板條寬度(b)、格柵板條中心距(d)和格柵斷面模型之間的相對距離(xg)，獲得A，B和C 3類格柵紊流場。其中，A 類和B 類紊流場的紊流積分尺度相似，但紊流強度不同；B 類和C 類紊流場的紊流強度相似，但紊流積分尺度不同。A 類和B類紊流場采用6×6 的正方形方格，格柵板條寬度b為0.07 m，格柵板條中心距d為0.5 m；C類紊流場采用5×5的正方形方格，格柵板條寬度b為0.14 m，格柵板條中心距d為0.6 m。5×5 格柵和6×6 格柵試驗照片如圖3所示。各類格柵紊流場設置參數如表2所示。

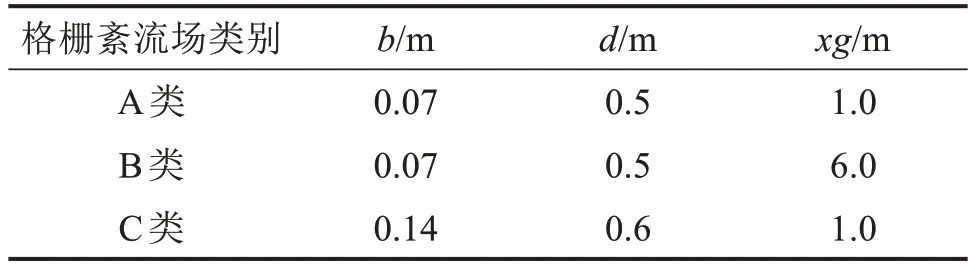
表2 3類格柵紊流場設置參數Table 2 Setting parameters of three kinds of grid turbulence flow field

圖3 格柵試驗照片Fig.3 Photos of grid test

為保證試驗結果的準確性，試驗中沿x軸方向連續布置12 個風場參數測試截面，根據測試結果計算3類紊流場的紊流度和紊流積分尺度，結果表明，對于各類格柵紊流場，隨著測試截面與格柵之間距離的增加，紊流度呈緩慢減少的趨勢，紊流積分尺度的變化呈現一定的波動性，但整體呈緩慢增長的趨勢。對比3 類格柵紊流場可以看出，A 類和B 類格柵紊流場紊流積分尺度相似，而紊流度不同，相差大約為2 倍；B 類和C 類格柵紊流場紊流度相似，而紊流積分尺度不同，相差大約為3倍。

2.3 試驗參數設置

本文利用車橋測力、測壓以及脈動風速同步測量系統，在A，B 和C 等3 類格柵紊流場內對車橋耦合工況進行風洞試驗，每個車橋耦合工況風攻角變化范圍為-3°，0°和3°，風洞試驗給定風速為9 m/s，工況列表如表3 所示，來流方向、主桁架和車道相對位置關系如圖4所示。

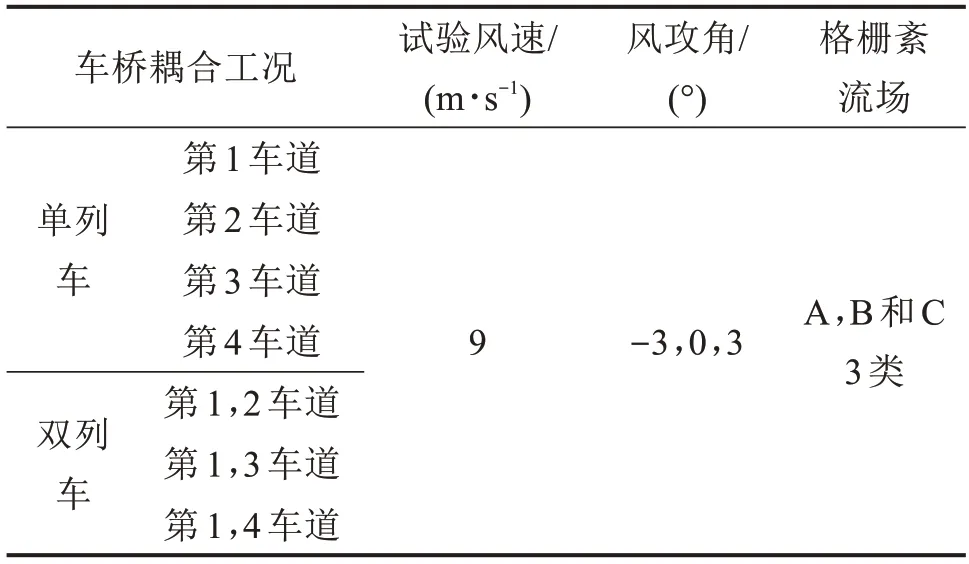
表3 格柵紊流場工況列表Table 3 Grid turbulent flow condition list

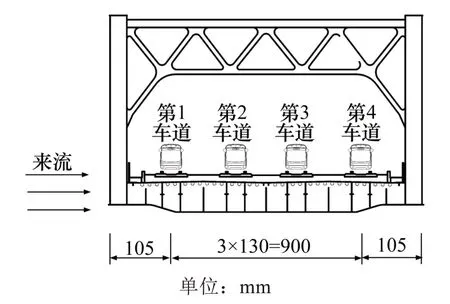
圖4 來流方向、主桁架和車道相對位置示意圖Fig.4 Schematic diagram of incoming flow direction,main truss and relative position of lane

由于對氣動導納識別要求測力數據與風速數據同步，眼鏡蛇風速探頭應盡可能靠近試驗模型，同時不能受試驗模型的干擾，為確定眼鏡蛇風速儀的固定位置，在B類風場中，利用移測架測試眼鏡蛇風速儀在迎風側桁架腹桿平面內、距桁架梁頂面不同距離的風參數數據，測試距離范圍為0～35 cm，變化步長為5 cm，測試試驗安裝如圖5所示。

圖5 試驗模型沿高度干擾區域測試圖Fig.5 Test diagram of test model along height interference area

圖6 為距離模型頂面不同高度處，風速u和w分量紊流度隨距離的變化曲線。由圖可知，眼鏡蛇風速儀當距離節段模型頂面較近時，紊流度較大；隨著距離的增大，紊流度快速減小，當距離大于10 cm 時，紊流度趨于穩定，說明此時已不再受到節段模型表面分離流的干擾。因此將眼鏡蛇風速儀固定于距離模型頂面10 cm 處，如圖7所示。

圖6 不同高度處風場紊流度Fig.6 Turbulence degree of wind field at different heights

圖7 同步測量眼鏡蛇風速儀固定圖Fig.7 Fixed drawing of synchronous measurement cobra anemometer

3 列車抖振力氣動導納

3.1 不同攻角下的列車氣動導納

B 類風場中單列車位于2 號橋面位置時，根據不同風攻角下列車B測壓截面的抖振力譜，并結合脈動風譜以及抖振力-脈動風交叉譜，對列車氣動導納函數進行識別計算，并與經典氣動導納Sears函數簡化式作比較。表4為用于氣動導納識別計算相應工況的三分力系數及其導數。圖8為不同風攻角下列車六分量氣動導納的識別結果。

表4 不同攻角下列車三分力系數及其導數Table 4 Three component coefficient and its derivative of train at different angles of attack

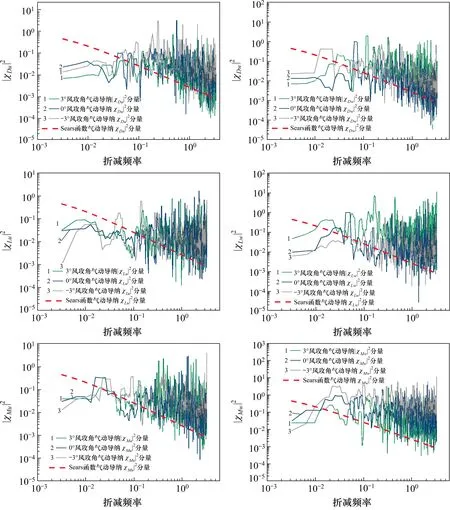
圖8 不同風攻角下單列車氣動導納Fig.8 Aerodynamic admittance of single train at different wind attack angles

由圖可知，不同風攻角下氣動導納各分量均具有相似的形態和特征，隨折減頻率的變化趨勢基本一致。同時可以看出，風攻角對氣動導納u分量影響不明顯，而對氣動導納w分量有一定的影響，以升力氣動導納為例，在折減頻率變化范圍內，u分量3°攻角氣動導納∣χMw∣2總和為0°攻角氣動導納∣χMw∣2總和的0.79 倍，w分量3°攻角氣動導納∣χMw∣2總和為0°攻角氣動導納∣χMw∣2總和的6.63倍，且u分量氣動導納分量模的平方值總體要小于w分量。Sears 氣動導納函數隨折減頻率的變化趨勢與列車各氣動導納分量在高頻區有一定的相似性，但數值均偏小，因此直接將Sears 函數用于列車抖振力的修正存在較大的誤差。同時注意到，在對氣動導納升力和升力矩的識別中，與順風向脈動風速u相關的識別結果有較大的離散性，其主要是由于抖振升力和升力矩主要受豎向脈動風速w的影響，從而造成綜合最小二乘法中殘量函數對u相關的導納分量的不敏感，使得相應識別結果的離散性較大。

3.2 不同格柵紊流場下單列車的氣動導納

3.2.1 紊流度對單列車氣動導納的影響

A 類和B 類格柵紊流場的紊流積分尺度相似，而紊流度相差較大，圖9 為紊流場A 和B 中在列車測壓截面處擬合的脈動風速u，w對氣動導納函數各分量模的平方。從圖中看出，對于∣χDu∣2，∣χDw∣2，∣χLw∣2氣動導納分量，在低頻區域紊流度的影響較小，隨著折減頻率的增大，不同紊流度下得到的氣動導納模越大；對于∣χLu∣2氣動導納分量，在所關心的折減頻域內不同紊流度下氣動導納模的差別均較大。同時注意到，紊流度對列車氣動導納分量∣χMu∣2和∣χMw∣2的影響相對較小，且隨著折減頻率的增加，不同紊流度下氣動導納模的大小趨于一致。

從總體上看，紊流度對列車氣動導納各分量具有不同程度的影響，幾乎在所關心的折減頻率全部范圍內，在A 類格柵紊流場中識別出的列車氣動導納函數各分量模的平方均大于格柵紊流場B中的結果，產生這種現象的原因很可能與A 和B 2類格柵紊流場中紊流度不同造成的。紊流場中具鈍體截面和流線型截面周圍的流場具有很大的不同，對于流線型截面，流場幾乎完全附著，作用于結構上的力與來流紊流直接相關；而對于鈍體截面，流場在截面附近不斷分離再附，其特征紊流在結構周圍的發展對結構抖振力有不可忽視的影響。因此，紊流度在一定范圍內的變化改變了特征紊流，從而使測量得到的抖振力發生改變，進而對氣動導納產生影響。

3.2.2 紊流積分尺度對單列車氣動導納的影響

B 類和C 類格柵紊流場的紊流度相似，而紊流積分尺度相差較大，圖10 為紊流場B 和C 中在列車測壓截面處擬合的脈動風速u，w對氣動導納函數各分量模的平方。從圖10 中可以看出，C 類格柵紊流場中各氣動導納分量模的平方基本大于B類紊流場中的相應值。造成以上現象的主要原因可能是由于氣動導納在抖振頻域理論中是用以對隨機脈動風荷載的非定常特性和沿結構寬度方向的不完全相關性來進行修正，紊流積分尺度越大(C類格柵紊流場)，脈動風荷載沿列車寬度方向的相關性越好，非定常特性越弱，因此氣動導納模的平方在頻域范圍內也越大。

對于∣χDu∣2，∣χDw∣2氣動導納分量，紊流積分尺度的影響較小。不同紊流積分尺度的流場內，∣χLu∣2的差別隨著折減頻率的增大逐漸減小，最后趨于一致；而∣χMw∣2卻具有相反的分布規律，在低頻區差別較小，在高頻區差別較大。同時可以注意到，∣χMu∣2分量在不同紊流場內的差值在折減頻率變化范圍內基本一定。特別地，對于氣動導納∣χLw∣2分量，在低頻區，紊流積分尺度越大，氣動導納分量模的平方越小；而在高頻區，紊流積分尺度越大，氣動導納分量模的平方越大。由此可見，不同氣動導納分量受紊流積分尺度影響的程度和變化規律略有不同，紊流積分尺度對氣動導納模的平方值的影響在不同頻域范圍內均有不同程度的差異。

根據A，B 和C 3 類格柵紊流場中列車氣動導納識別和擬合，通過分析比較可以看出，紊流度和紊流積分尺度對運行于桁架內部列車的氣動導納函數各分量具有不同程度的影響，因此，在對列車氣動導納的識別中需要同時考慮紊流度和紊流積分尺度與實際情況的相似性，否則會造成較大的偏差。

3.3 不同格柵紊流場下雙列車的氣動導納

3.3.1 紊流度對雙列車工況背風側列車氣動導納的影響

A 類和B 類格柵紊流場的紊流積分尺度相似，而紊流度相差較大，圖11 為雙列車分別位于1 號和2 號橋面位置時，針對于A 類和B 類紊流場，在背風側列車測壓截面處擬合的脈動風速u，w對列車氣動導納函數各分量模的平方值，對比分析紊流度對背風側列車氣動導納函數的影響。從圖中可以看出，在所關心的折減頻率幾乎所有的變化范圍內，紊流度對背風側列車氣動導納函數各分量均有較大的影響，且在折減頻率變化范圍內，風場內的紊流度越大，則列車氣動導納模越小，其原因可能與紊流場中紊流度的變化有關。同時注意到相較于單列車工況下列車氣動導納識別和擬合的相應結果，雙列車工況下背風側列車的氣動導納函數模更大，大部分情況下大于1，且對風場中紊流度的大小更加敏感，在相同的紊流度變化幅度下，背風側列車氣動導納函數模的平方值變化幅度更大。

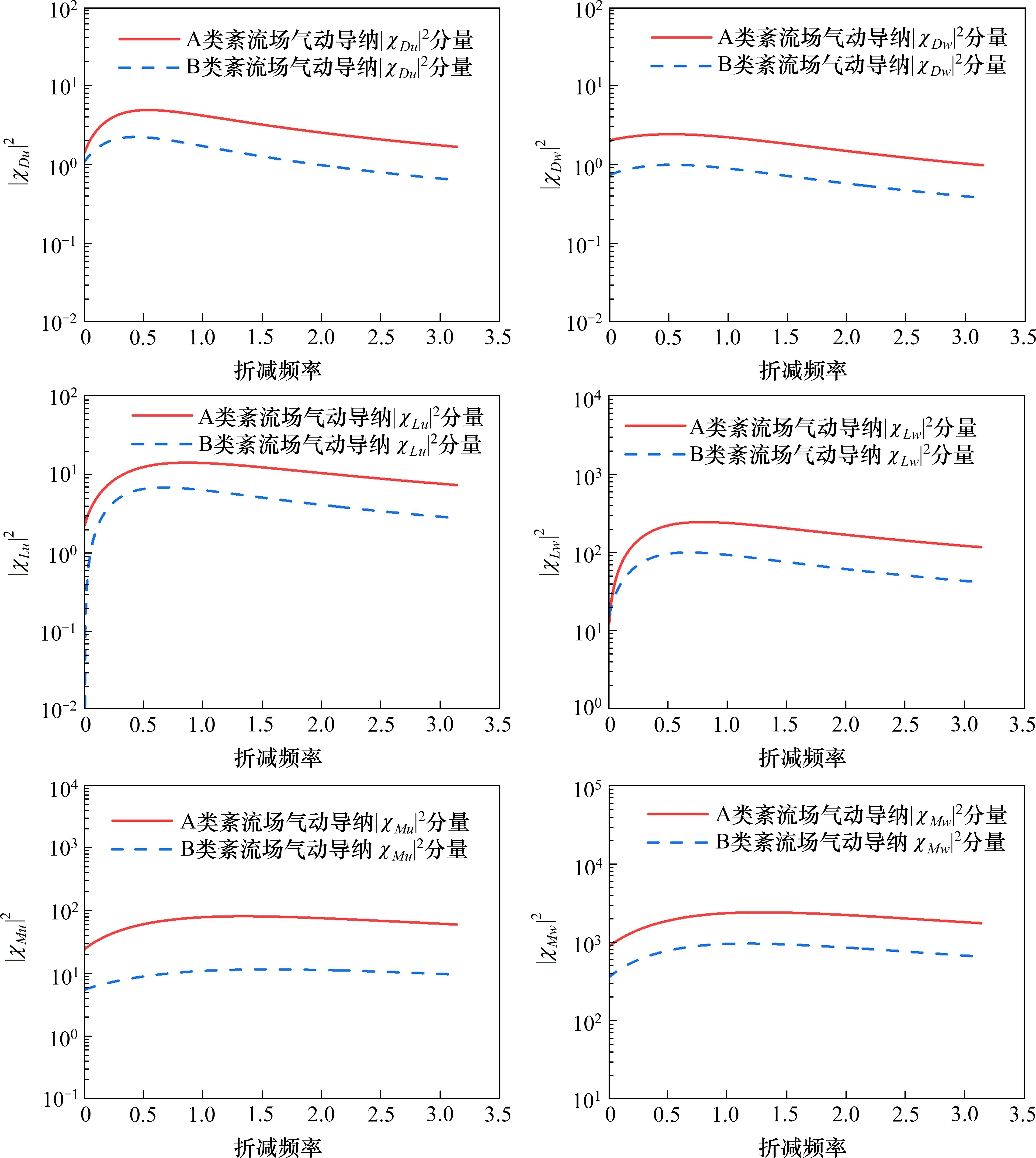
圖11 A類和B類風場下背風側列車氣動導納函數Fig.11 Aerodynamic admittance function of train on leeward side in type A and type B wind fields

3.3.2 紊流積分尺度對雙列車工況背風側列車氣動導納的影響

B 類和C 類格柵紊流場的紊流度相似，而紊流積分尺度相差較大，圖12 為雙列車分別位于1 號和2 號橋面位置時，針對于A 類和B 類紊流場，在背風側列車測壓截面處擬合的脈動風速u和w對氣動導納函數各分量模的平方值，對比分析紊流積分尺度對背風側列車氣動導納函數的影響。

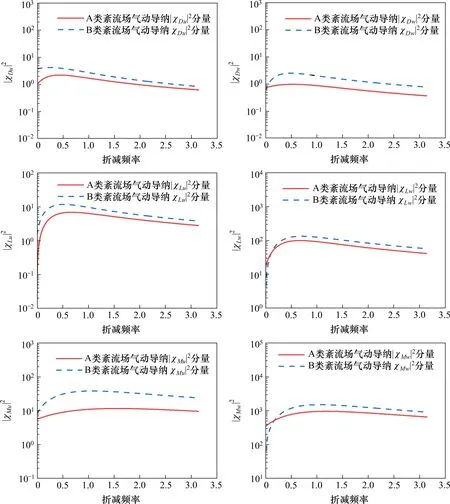
圖12 B類和C類風場下背風側列車氣動導納函數Fig.12 Aerodynamic admittance function of train on leeward side in B and C wind fields

從圖中可以看出，在所關心的折減頻率幾乎所有的變化范圍內，紊流積分尺度對背風側列車氣動導納函數各分量均有一定的影響，且在折減頻率變化范圍內，風場內的紊流積分尺度越大，則列車氣動導納函數模的平方值越大，其原因可能與單列車工況下一致。

同時注意到，與紊流度相比，紊流積分尺度對背風側列車的氣動導納的影響略小，在不同紊流積分尺度的風場中計算識別得到的氣動導納模的差別較小，因此背風側列車的氣動導納函數對風場內紊流積分尺度的變化不敏感，這可能是受到迎風側列車遮擋的原因。除此之外，所關心的幾乎所有折減頻率范圍內，不同紊流積分尺度風場內列車氣動導納之間的差別趨于定值，氣動導納函數曲線隨著折減頻率的變化平行發展。

4 結論

1)遺傳算法可以對自譜-交叉譜總體最小二乘法取得良好的計算結果，風攻角的變化對列車氣動導納u分量影響不明顯，以升力氣動導納為例，在折減頻率變化范圍內，u分量3°攻角氣動導納∣χMw∣2總和為0°攻角氣動導納∣χMw∣2總和的0.79 倍，w分量3°攻角氣動導納∣χMw∣2總和為0°攻角氣動導納∣χMw∣2總和的6.63 倍。除此之外，Sears 函數在高頻區與列車氣動導納識別結果具有一定的相似性，但數值均偏小。

2) 來流紊流的紊流度和紊流積分尺度的變化對單列車工況和雙列車工況背風車的氣動導納均有不同程度的影響，因此，在對列車氣動導納識別的風洞試驗中需考慮紊流度和紊流積分尺度的相似性。

3) 背風側列車氣動導納模具有明顯的波峰，且值大于單列車工況氣動導納相應識別結果，大部分情況下大于1。