明確問題指向，促進有效教學

王穎

[摘 要]目前，課堂教學中的問題設計依然存在著指向不明、片面追求數量、質量不高等問題。從問題設計的指向性角度提出優化問題設計的基本途徑，以啟迪學生思維，發展學生數學素養。

[關鍵詞]問題;設計;指向性;小學數學

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2022）05-0087-03

愛因斯坦曾言，提出一個問題往往比解決一個問題更重要。教師恰到好處的提問，能夠引起學生的好奇心和思考欲，燃起學生對知識的探究熱情。然而，目前的課堂教學問題設計依然存在著指向不明、片面追求數量、質量不高等問題。筆者從問題設計的指向性角度論述優化課堂提問策略的基本途徑，以期能夠起到拋磚引玉的作用。

一、指向比較，探尋知識緣由

教育家烏申斯基認為，比較是一切理解和思維的基礎，我們正是通過比較來了解世界上的一切。基于小學生的認知規律，小學數學教材在編排上呈現出明顯的螺旋式上升的特點，不同年級、不同學段的數學知識看似是一個個獨立的模塊和單元，實則前后內容之間具有密切的關系。教學中，教師在提問時應指向前后知識的異同點，通過比較，能夠使學生了解知識的來龍去脈，把握知識的內在邏輯關聯，從而幫助學生獲得對知識的深刻理解，最終促進學生的深度學習。

【例1】“異分母分數加減法”教學片段

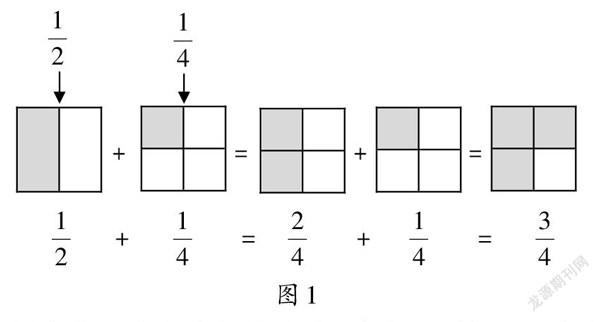
師：我發現不少同學寫出算式1/2+1/4=1+1/2+4=2/6=1/3，這是錯誤的。那么，為什么同分母分數可以直接相加減，而異分母分數不能直接相加減？

生1：因為分母不同，分數單位不一樣，所以不能直接相加減。

師：為什么分數單位不一樣就不能直接相加減？有人能為我們詳細解釋嗎？

生2：比如，1元和2元加在一起是3元，因為它們的單位都是元，但是1元加2角既不是3元也不是3角，它們的單位不同，不能直接相加減。分數的加減法也是同樣的道理，同分母分數的分數單位相同，可以直接把分子相加減，而異分母分數的分數單位不同，不能直接相加減。

生3：我們在學習整數加減法時，把相同數位上的數字相加減，即把個位上的數字和個位上的數字相加減，十位上的數字和十位上的數字相加減，這是因為相同數位上的數字單位都相同，比如個位上的5都表示5個一，十位上的3都表示3個十。

師：那應該如何解決這個問題呢？

（學生在討論后一致認為，應該用通分的方法把異分母分數轉化為同分母分數，這樣分數單位相同了，就可以直接按照“同分母分數加減法”的運算法則進行計算，如圖1所示）

教師問題設計的指向性決定了學生思考的方向，也決定了學生思考的深度。教師從“同分母分數加減法”和“異分母分數加減法”的異同切入，巧妙設計問題，既找到了前后知識之間的聯系，又使學生能夠從分數單位的角度思考問題，從而獲得對知識的本質認識，使學生不但知其然，而且知其所以然。

比如，在教學“筆算除法”時，教師往往將教學聚焦在除法豎式中每一步計算的算理上，力圖讓學生在理解算理的基礎上把握豎式計算的方法。這樣的教學自然是無可厚非的，然而，在此基礎上，教師不妨提出這樣的問題：“在學習乘法豎式時，我們是從低位開始計算，但是為什么在學習除法豎式時，卻要從高位開始計算呢？”然后，教師引導學生以16×3和56÷2為例進行探討。學生通過探討會發現，乘法豎式之所以要從個位算起，是為了更好地處理進位，這是由數學中滿十進1的規則決定的。關于為什么除法豎式要從高位計算，教師可以采取“試錯”的策略，讓學生嘗試先從個位計算。這時候，學生發現56÷2個位商3，但是十位上的5并不能被2整除，這樣就遇到了問題。然后，教師引導學生轉換思路，嘗試從十位除起，學生就能體會到從高位除起方便處理余數。

教師將問題指向乘法豎式和除法豎式算法的合理性，使學生通過對比和分析，對這些知識有了更加深刻的認識，從而促進深度學習的發生。

二、指向根源，探尋知識本質

《道德經》中有言：“道生一 ， 一生二 ， 二生三 ， 三生萬物。”這里的“道”，可以理解為事物的本質。小學生以形象思維為主，在把握知識本質方面往往會感到力不從心，對知識的認識往往淺顯化，只能達到“所見即所得”“就事論事、就題論題”的層次。在教學中，教師問題的設計應該指向知識的本質，使學生透過知識的表面現象深入挖掘，領悟知識的本質，從而增強對知識的認知，提升數學理解力。

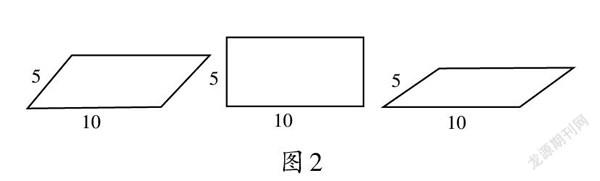
比如，在教學“四邊形的不穩定性”時，筆者會引導學生進行實驗一：用四根木棒做成一個四邊形框架，再用手拉動這個四邊形框架，四邊形框架就會變形。據此，筆者引導學生得出結論：四邊形具有不穩定性。細細想來，這個實驗不免令人生疑：能用手拉動框架就說明四邊形具有不穩定性嗎？為此，筆者進一步優化了教學設計，在上述步驟的基礎上引入了實驗二：筆者引導學生用四根硬紙條做一個四邊形框架，把四邊形框架各頂點上的兩條邊都粘在一起，然后讓學生用手拉動四邊形框架。學生發現這個四邊形框架不會變形，但如果用力過猛，就會把四邊形框架拉破。筆者提問：“實驗二中的四邊形框架不容易變形，是不是說明四邊形也具有穩定性呢？我們應該如何理解不穩定性？”學生討論后，筆者引入實驗三：讓學生用2張長5厘米的紙條和2張長10厘米的紙條拼成四邊形，看看各個小組拼成的四邊形是否一樣。學生通過實驗三發現，盡管使用的實驗材料相同，但是拼成的四邊形卻各不相同（如圖2）。據此，筆者總結：“我們所說的四邊形易變形或具有不穩定性，指的是盡管四邊形的四條邊的長度都確定了，但是它的形狀卻是可以變化的。”

在實際教學中，不少學生在理解三角形的穩定性和四邊形的不穩定性時，往往得出“拉不動就是具有穩定性，拉得動就是具有不穩定性”的結論。學生的認識如果止步于此，就說明他們還沒有觸及知識的本質。教學中，筆者采取對比實驗法，針對“什么是不穩定性”這一問題巧妙設問，使學生意識到四邊形的不穩定性并非簡單的“拉得動，易變形”，并理解不穩定性指的是“盡管四邊形的四條邊的長度都確定了，但是它的形狀卻是可以變化的”，進而消除了學生的認知誤區，使學生獲得了對知識的本質認識。

三、指向應用，明確知識價值

數學從生活中來，最終為現實生活服務。數學家華羅庚曾說：“宇宙之大，粒子之微，火箭之速，化工之巧，地球之變，生物之謎，日用之繁，無處不用數學。”從認識論的角度看，數學學習的過程是一個從感性認識到理性認識的過程，而從理性認識到實踐是認識的又一次意義更為重大的飛躍。讀書是一種學習，實踐也是一種學習，而且是一種更為重要的學習。教學中，教師應該轉變“知識本位”的教學思想，在設計問題的過程中，關注知識的實際應用，培養學生理論聯系生活的能力，發展學生的應用意識，使學生感受到數學學習的價值。

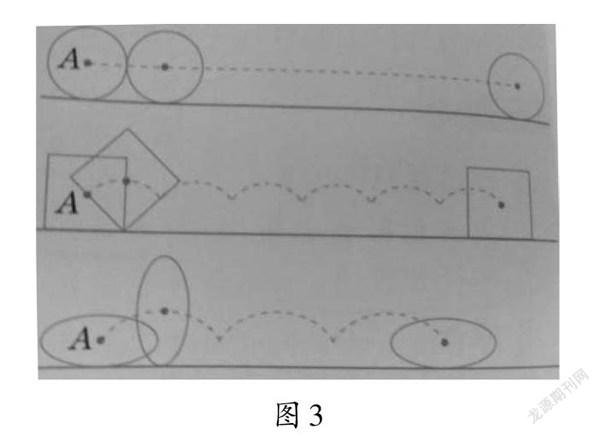
比如，在教學“圓的認識”時，筆者設計了這樣的問題：“為什么自行車、摩托車、小汽車的車輪都設計成圓形？為什么不把車輪設計成正方形或者橢圓形？”學生結合教材內容展開了分析和討論，得出結論：如圖3，點A代表車軸，當正方形車輪和橢圓形車輪滾動時，在不同位置軸心到地面的高度不相等，點A的運動軌跡是曲線，這會導致車輪滾動起來后車子比較顛簸，不平穩;而圓形車輪在滾動時，軸心到地面的高度就是圓的半徑，圓的半徑是始終不變的，所以使用圓形車輪，車子在運動的時候是平穩的。

教學中，筆者把圓的特征和生活實例相結合，設計了具有趣味性和知識性的問題，實現了數學知識與生活應用的對接，讓學生帶著熱情去學習新知識，不但使學生加深了對圓的特征的理解，還使學生意識到數學知識在現實生活中的應用價值。

【例2】“三角形的穩定性”教學片段

師：生活中哪些物體中含有三角形？

生1：自行車車架、籃球架和電線桿架等。

師：這些物體中的某些部位為什么要設計成三角形？

生2：這樣比較牢固，不容易變形。

（教師出示橋梁、衣架、金字塔等圖片）

師：既然三角形這么好，我們學校的電動伸縮門為什么不做成三角形的呢？

生3：做成三角形的不方便打開和關上。

師：三角形和四邊形各有特點，在運用時要根據實際情況選擇，這樣才能讓它們為人類造福。

教學中，筆者以數學與生活的聯系作為切入點設計問題，引導學生分析三角形的穩定性在現實生活中的運用，架設起知識與生活之間的橋梁，使學生感受和體驗到數學的價值與魅力，并在對知識的應用中促進對知識的理解。

四、指向整體，促進知識建構

蘇霍姆林斯基曾言，揭示未知和已知之間的深刻聯系，是培養學生對知識的興趣的教育訣竅之一。由于課時劃分等現實因素的影響，數學教材不得不把原本緊密相連的知識劃分成一個個單元和章節，以方便教師分課時完成教學任務。這樣就使得學生通過每課時獲得的知識是相對獨立的，學生難以真切體會知識點之間的聯系，這不利于學生從整體上理解知識。實際上，數學學科知識具有較強的關聯性，新知識往往是舊知識的延伸和發展，同時又成為學習后續知識的基礎，舊知識與新知識相互關聯，形成了一個系統性的知識網絡。在教學中，教師問題的設計應指向整體，幫助學生建立起新舊知識之間的聯系，從而促進學生對知識的整體建構。

【例3】“認識平行四邊形”教學片段

（教師引導學生拉動長方形框架，使長方形變成不同的平行四邊形，然后再拉動框架使平行四邊形變成長方形）

師：請同學們說一說平行四邊形、長方形和正方形三者之間的關系。

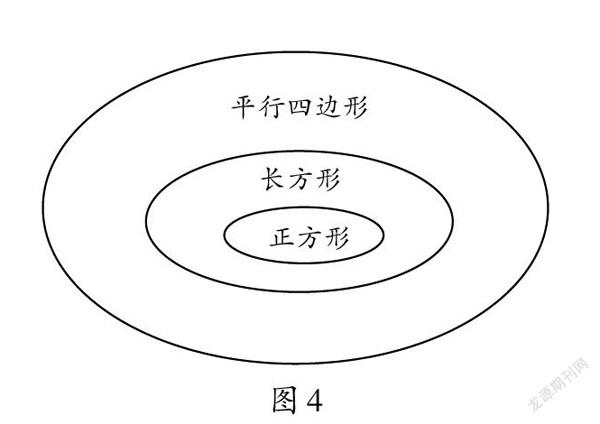
生1：我通過比較，發現平行四邊形和長方形的相同點是兩組對邊分別平行，因此，長方形也具備平行四邊形的特征，屬于平行四邊形，但是長方形四個角都是直角，因此長方形是一種特殊的平行四邊形。正方形兩組對邊分別平行，四個角都是直角，因此正方形也是特殊的平行四邊形。而且正方形除了具備長方形的特點，還具有四條邊相等這一特殊性質，因此正方形是特殊的長方形（如圖4）。

教學中，筆者從平行四邊形、長方形和正方形三者的異同點入手，精心設計問題引發學生思考，學生在分析和探究中主動把平行四邊形的知識建構在長方形和正方形的知識基礎上，從而實現了三者的有效聯系和貫通，有利于學生從整體上學習知識，從而促進學生對知識的整體理解。

在教學“多邊形的面積”時，筆者在學生掌握了平行四邊形、三角形和梯形的面積公式后，引導學生發現它們之間的關系。筆者提出問題：“你能用梯形面積公式計算三角形和平行四邊形的面積嗎？”學生感到困惑，這三個圖形的面積公式各不相同，怎么能用同一個公式計算呢？這個時候，筆者通過多媒體，演示梯形上底的兩個端點逐漸靠近，最后重合成一個點，這樣梯形就變成了三角形（把三角形看成是一個上底是0的特殊梯形）;梯形的下底逐漸縮短，上底逐漸變長，當上底和下底相等時，梯形就變成了平行四邊形（把平行四邊形看成是上底和下底相等的特殊梯形）。有了這樣的鋪墊，學生自然就能夠理解梯形的面積公式同樣適用于三角形和平行四邊形，是一個“萬能公式”。

教學中，教師創設問題情境，激發學生認知沖突，然后通過動態演示，有效地溝通了梯形、三角形和平行四邊形之間的內在聯系，使學生的視線不再局限于一個個具體的多邊形，而是用更加宏觀的視野對知識進行理解和定位，由此建構起多邊形面積公式的知識體系，學生的思維自然也就會向更深處漫溯。

問題對學生的思維具有重要的催動和引發功能。在教學中，教師在設計問題時應明確問題的指向性，使問題設計更具針對性，以便更好地啟迪學生思維，發展學生數學素養。

（責編 楊偲培）