重心向量式的推廣及應用

江鏡 戴宏照

[摘? 要] P是△ABC的重心的充要條件是++=0，重心把△ABC分成面積相等的三個小三角形. 由此推廣到三角形所在平面任意點P的“奔馳定理”：設點P是△ABC內（含邊界）任意一點，記△PBC，△PCA，△PAB，△ABC的面積分別為S，S，S，S，則S·+S·+S·=0. 應用“奔馳定理”及其推論可以快速地求解有關三角形面積比值的問題. 根據類比推理，還提出了一個有關三棱錐的猜想.

[關鍵詞] 奔馳定理;重心向量式;面積;猜想

我們都知道，點P是△ABC的重心的充要條件是++=0，重心把△ABC分成面積相等的三個小三角形，如果記△PBC，△PCA，△PAB，△ABC的面積分別為S，S，S，S，即S=S=S，可以看作S·+S·+S·=0. 那么，對于△ABC所在平面內任意一點P，以上結論是否成立呢？

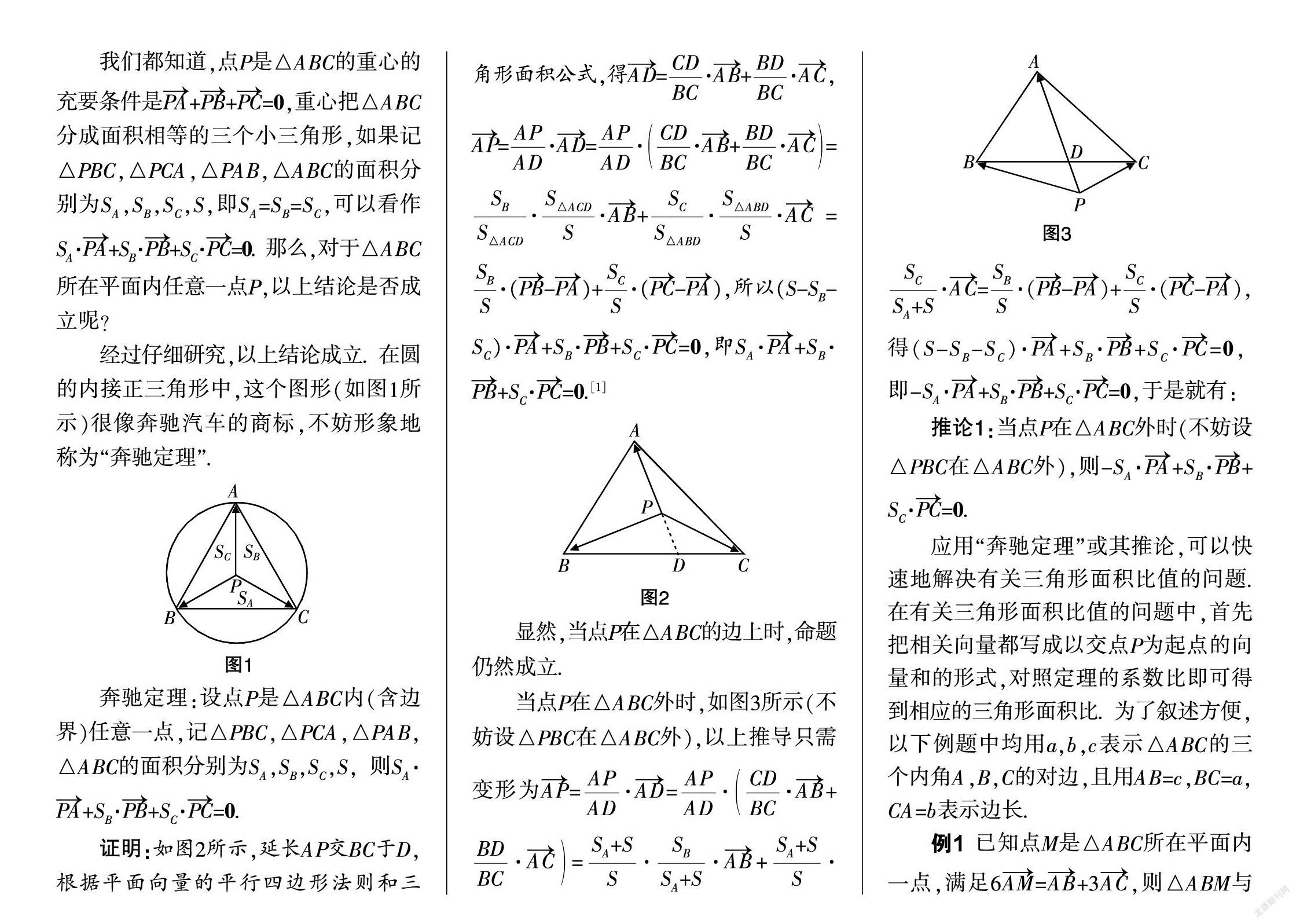
經過仔細研究，以上結論成立. 在圓的內接正三角形中，這個圖形（如圖1所示）很像奔馳汽車的商標，不妨形象地稱為“奔馳定理”.

奔馳定理：設點P是△ABC內（含邊界）任意一點，記△PBC，△PCA，△PAB，△ABC的面積分別為S，S，S，S，則S·+S·+S·=0.

證明：如圖2所示，延長AP交BC于D，根據平面向量的平行四邊形法則和三角形面積公式，得=·+·，=·=·

·+·

=··+·· =·（-）+·（-），所以（S-S-S）·+S·+S·=0，即S·+S·+S·=0.[1]

顯然，當點P在△ABC的邊上時，命題仍然成立.

當點P在△ABC外時，如圖3所示（不妨設△PBC在△ABC外），以上推導只需變形為=·=·

·+·

=··+··=·（-）+·（-），得（S-S-S）·+S·+S·=0， 即-S·+S·+S·=0，于是就有：

推論1：當點P在△ABC外時（不妨設△PBC在△ABC外），則-S·+S·+S·=0.

應用“奔馳定理”或其推論，可以快速地解決有關三角形面積比值的問題. 在有關三角形面積比值的問題中，首先把相關向量都寫成以交點P為起點的向量和的形式，對照定理的系數比即可得到相應的三角形面積比. 為了敘述方便，以下例題中均用a，b，c表示△ABC的三個內角A，B，C的對邊，且用AB=c，BC=a，CA=b表示邊長.

例1 已知點M是△ABC所在平面內一點，滿足6=+3，則△ABM與△BCM的面積比為_______，若△ABC的面積是12，則△MAC的面積是_______.

解析：把已知條件化成起點是M的向量得-6=（-）+3（-），即2++3=0. 由“奔馳定理”得==;==，得S=2.

例2 在平面四邊形ABCD中，△ACD的面積是△ABC面積的2倍，數列{a}滿足a=3，且（a-3）=+（a-2），則a=_______.

解析：把已知條件變形為-（a-3）+（a-2）=0，把C看作△ABD外一點，由“推論1”可知S∶S=S∶S=（a-3）∶（a-2）=2，可得a=2a-1，即得a-1=2（a-1），所以a-1=（3-1）2n-1，即a=2n+1，因此a=257.

若把“奔馳定理”看作是重心向量式的推廣，則可把重心向量式看作是“奔馳定理”的“推論2”.

推論2：若點G是△ABC的重心，則++=0，反之也成立.

例3 已知G為△ABC所在平面內一點，點M，N分別在邊AB，AC上，滿足3++=+-，=x+y，其中x+y=1. 若=，則△ABC和△AMN的面積比為_______.

解析：如圖4所示，由3++=+-可得-3+-=2=2-2，即++=0，所以G是△ABC的重心. 設=λ，可得=（+）=+λ，所以x=，y=λ. 又x+y=1，所以λ=，所以=，則==·=.

當點I是△ABC的內心時，記內切圓的半徑為r，由此可得S=ar，S=br，S=cr，于是就有：

推論3：若點I是△ABC的內心，則a+b+c=0.

例4 已知△ABC的內切圓I，且++=，△ABC的周長是18，則△ABC的面積是_______，其內切圓的面積是_______.

解析：把++=變形為3+2+4=0，根據推論3可設a+b+c=3k+2k+4k=18，所以k=2，即a=6，b=4，c=8.所以cosC==-，sinC=，所以S=×6×4×=3. 又S=×18r=3，得r=，所以S=πr2=.

當點O是△ABC的外心時，記OA=OB=OC=R，根據圓周角與圓心角之間的關系可得S=R2sin2A，S=R2sin2B，S=R2sin2C，于是就有：

推論4：若點O是△ABC的外心，則sin2A·+sin2B·+sin2C·=0.

例5 已知△ABC的外接圓O的半徑為1，且3+4+5=0，則△ABC的面積是_______.

解析：因為O是外心，即OA=OB=OC=1，把3+4=-5平方后可得·=0，即<，>=2C=，于是有sin2A∶sin2B∶sin=3∶4∶5，則sin2A=，sin2B=，所以S=sin2A+sin2B+sin2C=.

當點H是△ABC的垂心時，AH⊥BC于D，如圖5所示，則 tanB=，tanC=，所以==，同理可得=. 因此S∶S∶S=tanA∶tanB∶tanC，于是就有：

推論5：若點H是△ABC的垂心，則tanA·+tanB·+tanC·=0.

例6 點H是△ABC的垂心，且滿足+2+3=2，c=，則△ABC的面積S=_______.

解析：由+2+3=2得+2+3=2-2，即3+2+=0.根據推論4可設tanA=3k，tanB=2k，tanC=k，k>0，由-tanA=tan（B+C）得= -3k，解得k=1. 所以tanA=3，tanB=2，tanC=1，進而得到sinA=，sinB=，sinC=. 由正弦定理知a=3，b=4，c=，因此S=×3×4×=6.

需要注意的是，在應用“奔馳定理”或其推論時，首先要把已知條件轉化為以特殊點P為起點的向量等式x+y+z=0的形式，，，的系數比是x∶y∶z=（±）S∶S∶S，不一定恰好是對應的面積S=

x

，S=y，S=z，推論中亦如同此理.

按照從平面到空間的認知規律，猜測在三棱錐中應該有類似的結論，即在三棱錐A-BCD內一點P，記三棱錐P-BCD，P-CDA，P-DAB，P-BAC的體積分別為V，V，V，V，應有V·+V·+V·+V·=0成立;當點P在三棱錐A-BCD外（不妨設點P與點A位于平面BCD異側），應有-V·+V·+V·+V·=0成立.

參考文獻：

[1]? 裴珊珊，陳德富，李霞. “奔馳定理”的多種證法及其應用[J]. 中學數學研究，2018（12）：48-49.