有效開展教學活動,類化遷移求得真知
高吉忠

[摘? 要] 數學活動課能激發學生的學習興趣,能推動學生發現問題和解決問題,從而求得真知. 在教學中,教師應關注數學活動課的開展,依據學情,依托校情,結合教材和實際情況精心設計數學活動課,讓學生體會知識的發生過程,開闊視野,發展思維.
[關鍵詞] 數學活動;思維;實踐
數學活動課是學生探索數學知識如何與實踐相結合的重要橋梁,因此重視數學活動課的開展,可以幫助學生有效地拓展思維,感受數學思想. 在日常教學中,受授課時間、教師的教學觀念、活動開展的環境等客觀因素的影響,數學活動課很難受到教師的重視,使這一課程模式的作用沒有得到有效的發揮. 數學活動課應具有明確的目標和多角度的活動環節,從而讓學生通過數學活動課積累活動經驗,培養實驗操作能力和創新思維,實現全面發展. 本文以筆者的一節數學活動課為例,談一談數學活動課設計的策略,供大家參考.
研究教材,發現問題
數學活動課的開展仍然要以學生所學的知識為基礎. 在學習教材知識的基礎上,教師還要思考如何開闊學生的視野,使學生能多角度地思考問題,并解決其他類似問題. 為此,教師要仔細研究教材,從教材的基礎例題出發,思考如何開展數學活動課.
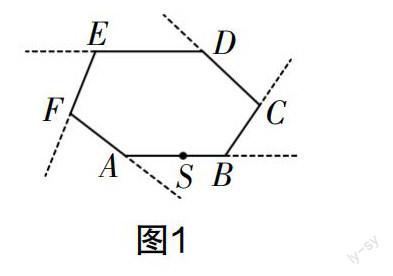
案例1如圖1所示,點S在六邊形環形跑道ABCDEF的邊AB上,小華從S點出發,繞六邊形一周后回到S點,請問:小明繞一周轉過的角度總和是多少?
“案例1”是一道數學與生活相聯系的試題,它把六邊形和生活中的環形跑道聯系起來,實際上跑步者繞跑道一周所轉過的角度就是六邊形的外角和. 因此大家可以想象,自己在跑道內部觀察,跑步者按照逆時針方向跑步,在頂點處轉彎所轉的角度都等于六邊形的一個外角,而這個數學模型不只可以求出六邊形的外角和,甚至所有凸多邊形的外角和都可以求出,且為360°.
通過凸多邊形的外角和,大家可以求出凸多邊形的內角和嗎?顯然,大家可以通過凸n邊形的內、外角和相加等于180°n,減去外角和360°,得到凸n邊形的內角和公式,即(n-2)×180°. 與傳統的將凸多邊形分割成三角形得到凸多邊形內角和公式的方法不同,這樣的研究方法更具有思維的發展性,其操作也更具有趣味性.
在研究此題的基礎上,教師要開拓思維,以此類推,除了研究凸多邊形,還要思考這樣的方法能否被應用在其他更加復雜的圖形上.
教師是學生的榜樣,教師的一言一行對學生都有潛移默化的作用,教師的思維方法對學生更起著引導作用,因此在解決問題時,教師要具有創新意識,這樣才能培養出具有創新思維的學生. “案例1”中,教師采用了與課本不同的求不規則多邊形外角和的方法,并將這種方法延伸至求多邊形的內角和,不僅使學生的思維得到了拓展,還激發了學生的探究興趣.
主動探索,激發興趣
數學活動課是一種探究課型,教師不能將它變成另一種講授的形式. 在教學中,教師要引導學生通過合作討論去主動探索解決問題的辦法,要讓學生不能過分依賴教師的提示和教師的直接幫助. 教師要精心設計問題,層層遞進地引導學生去發現問題,從而促進學生思維的開發.
案例2有趣的多角形.
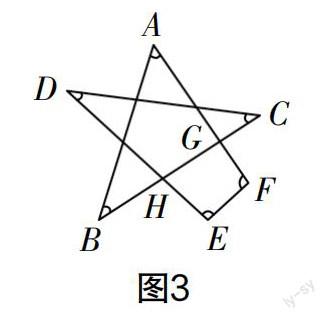
師:通過剛才的學習,我們已經知道求凸多邊形的內、外角和的方法,那你們可以求出五角形(如圖2所示)、六角形(如圖3所示)和七角形(如圖4所示)的內角和嗎?
學生小組討論、交流.
生1:我們可以運用分割法,將五角形分割成三角形,利用等量轉換,將五角形的五個內角匯聚到一個三角形中,這樣就可以得到五角形的內角和為180°.
師:那么六角形和七角形呢?
生2:求六角形和七角形的內角和時,我們同樣可以運用分割法,把它們分割成三角形或四邊形,然后利用等量轉換來求解,這樣就可以求得六角形的內角和是360°,七角形的內角和是540°.
師:非常好,同學們對于運用分割法求內角和的方法掌握得都非常好,這也是一種比較常用的方法,但是老師也有個疑惑,如果圖形更加復雜,變成n角形呢?該如何解答?
學生小聲討論之后,得不到答案,陷入沉默.
“案例2”通過由淺入深的方式引導學生探討,即首先由較易的方式引入,激發學生的探究熱情,接著引入較難的問題,引發學生思考,達到思維的深化. 學生對于一般的分割證明法已經非常熟悉,如果只滿足于此,那么面對比較復雜的問題,分割法難以解決時,學生就會感覺困難,因此教師還要引導學生綜合考慮,嘗試其他方法,提高學生綜合解決問題的能力.
遷移類比,猜想證明
數學知識之間具有很強的邏輯聯系,教學中教師可以充分利用這一特點,讓學生運用已學的舊知識去學習新知識,在舊知識的基礎上進行探索和思考,這樣不僅能達到溫故知新的效果,還可以構建知識聯系,完善知識結構.
案例3探究n角形的內角和.
師:既然同學們覺得計算n角形的內角和有難度,那么我們不妨先來看一看已經計算出的多角形的內角和,看看有沒有規律可循.
經過統計,學生得到了表1,仔細觀察后發現了一些規律.
生1:縱向看,每增加一個角或者一條邊,內角和都增加了180°.
生2:橫向比較n邊形和n角形的內角和,我發現n邊形的內角和都比n角形的內角和多360°.
師:既然大家已經有了這兩個重大發現,結合我們前面已得的n邊形內角和公式,你們能不能大膽猜想n角形的內角和公式?
生3:n邊形的內角和公式是(n-2)×180°,根據前面的發現,我猜測n角形的內角和公式是(n-4)×180°.
師:大家觀察得都很仔細,思考得也很認真. 猜想是學習數學需要經歷的過程,但猜想過后,還得論證我們的猜想是否正確.
遷移對比,抓住本質
通過剛才的觀察,大家發現凸多邊形的內角和適宜采用分割的方法,因為其造型簡單,但是多角形的造型比較復雜,通過分割的方法求其內角和顯得比較煩瑣,既然無法直接求出多角形的內角和,那就換一種思路,比如通過多角形的外角和來求其內角和.
案例4證明多角形的內角和.
師:大家還記得我們一開始是如何求多邊形的外角和的嗎?
師:我們通過一個環形跑道進行了動態求解,那么這個方法能不能用來求多角形的外角和呢?
學生開始交流,部分學生在紙上開始畫環形跑道.
生1:老師,我們可以把五角形也想象成一個環形跑道,假如在內部觀察跑步者,跑步者從起點出發后回到起點,我們只需要看他跑了幾圈就能知道度數了.
師:很好,那么你們思考一下跑步者跑了幾圈吧!(教師展示出圖5幫助學生理解)
教室里大家討論的熱情高漲,有的說1圈,有的說2圈……
師:讓我們來一次情景重現吧. 請一位同學上黑板用你的手來模擬一下,大家慢慢一起數.
學生一起數后發現是2圈,教師再次帶領大家在空中比畫,確認是2圈.
師:那么大家再思考一下六角形和七角形呢?
學生再次對比六角形(如圖6所示)和七角形的環形跑道,發現都是2圈.
經過對比,學生明白了為什么橫向對比多邊形的內角和與多角形的內角和時,多邊形的內角和總是比多角形的內角和多360°,因為同樣的邊或角,多角形跑道總要比多邊形跑道多跑1圈,外角和的增加自然帶動了內角和的減少. 有了這個發現,學生自然明白多角形的內角和只要用180°n減去外角和(即720°)就可以了.
歸納總結,自我反思
經過上述分析,學生學會了如何計算多角形的內角和,于是教師可以進行深度拓展,檢測學生的學習情況.
案例5? 七角形的內角和.
師:請同學們仔細觀察圖7所示的七角形,求這個七角形的內角和.
學生思考后發現跑步者需要跑3圈,于是得出求其內角和的方法.
經過上述探究,對于多邊形、多角形的內、外角和的研究方法,學生已經非常熟悉. 這樣的研究方法可以繼續指導學生在研究其他復雜問題時如何拆解并進行遷移類比.
本次活動課教師先引導學生從多邊形的外角和開始探究,然后探究多邊形的內角和,接著探究多角形的外角和,最后探究多角形的內角和,層層遞進,環環相扣,既充滿樂趣又充滿挑戰,符合學生的認知規律和發展特點,激發了學生的學習興趣. 這樣的活動課是學生思維發展的起點,至于如何進一步發展學生的能力,增強學生的學習主動性和積極性,還有賴于教師不斷探索和開發.

