對接舊知,循“序”漸進,建模生長
蔡中婷




摘要:“移多補少”是指研究具有相差關系的兩個量,把多的量移給少的一部分,從而使兩個量相等的一類問題。文章以“移多補少”拓展性學材開發為例,探究了提升學生思維能力的方法。
關鍵詞:小學數學? 促生長? “移多補少”? ?學材開發
一、對接舊知:喚經驗
舊知是新知的基礎,會對新知的學習產生影響。因此,在編寫拓展性學材時,教師應該對接舊知,激活學生的學習經驗。
課本銜接:
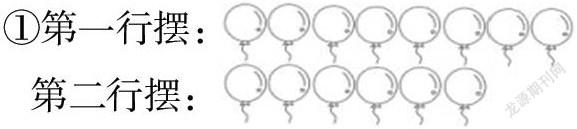
①第一行擺:
第二行擺:
第一行比第二行多_____個氣球,第二行比第一行少_____個氣球。
②明明有5張郵票,東東有12張郵票,東東和明明相差_____張郵票。
解決“移多補少”問題,討論的是相差數和移動數之間的關系,有時候問題還涉及根據相差數和一個量求另一個量。因此,筆者設計了一組相差數問題,從象形圖入手,再到文字表征,契合學生的認知規律,為之后“移多補少”的學習做好基礎鋪墊。
二、循“序”漸進:建模型
建構主義學習理論強調,教師的講解并不能直接將知識傳遞給學生,知識必須通過學生主動建構才能獲得。因此,教師必須構建序列型問題組,循“序”漸進,引導學生主動建構模型。
(一)從形入手,建表象
我們從形入手,給學生提供一個認知學習的“腳手架”,幫助學生建立知識表象,再逐漸過渡到抽象表征建模。
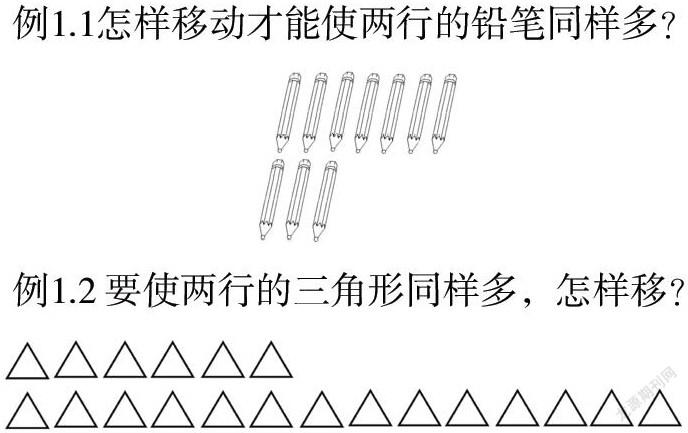
例1.1怎樣移動才能使兩行的鉛筆同樣多?
例1.2 要使兩行的三角形同樣多,怎樣移?
上述2個例題構成一組,讓學生在紙上“畫一畫”,如果有困難也可以借助小圓片動手“移一移”,在操作過程中,學生要先找到多出來的部分,然后把多出來的部分其中的一半移給少的。此時,教師的教學重點應落在追問上:“你是怎么移的?”獲取學生思維層次。第一層次:移錯,把多出來的部分全部移給少的;第二層次:知道不能把多出來的部分全部移給少的,會先一個一個少量移,結果正確但是不知道隱含的相差數和移動數之間的關系;第三層次:先找出相差數,再把多的部分平均分成兩份,一份留給自己,一份移給少的,明白其中的隱含關系。通過三個層次的對比,教師分層引導學生對比、討論,使學生初步建立“移多補少”的認知表象。
(二)動手操作,促認知
例2 動手剪一剪:把兩張不一樣長的紙條變成一樣長,不能丟棄任何一部分紙條。
通過上述在象形圖中移一移,學生已初步具備認知表象,但是部分學生對“移動數是相差數的一半”的認識不夠立體,所以通過剪紙帶的活動,教師將“移多補少”的方法進行半抽象化處理。學生剪出相差部分后,思考移動數時,不像之前的情況可以數出相差部分的數量嘗試著移,有“試誤”機會,而這里紙帶的長度未知,無法“試誤”,學生只能動手將多出來的部分對折,沿著折痕剪下后補給少的,兩段才會同樣長。“對折”這一操作巧妙地讓學生感悟到多出來的部分必須平均分成兩份,一份留給“自己”,一份移給少的,自然地過渡到“移動數是相差數的一半”的認知。
(三)從數到形,建模型
模型的建構從“形”到“數”,“形”為“數”提供表象支撐,“數”為“形”延伸理解深度。
例3.1 小明有10個蘋果,小紅有4個蘋果,小明要給小紅幾個,他們才會同樣多?
例3.2 小明比小紅多6個蘋果,小明要給小紅幾個,他們才會同樣多?
之前的例題都給學生提供了輔助的腳手架——象形圖,在圖的幫助下學生逐漸建立起“移動補少”的認知表象。此時,教師可以適時抽離“腳手架”,以數代形,將信息的表征方式改為文字,將形象認知轉化為抽象認知。不同層次的學生可能會有不同水平的解決方式:第一層次的學生可能會自己畫出象形圖,然后在圖上移一移;第二層次的學生可能直接找“相差數和移動數之間的關系”來求“移動數”。
例3.3 小明有10個蘋果,比小紅多6個蘋果,小明要給小紅幾個,他們才會同樣多?
正確的做法有兩種:第一種,先求出小紅的蘋果數量,再求出他們的差,再根據相差數求移動數;第二種,直接根據“小明比小紅多6個蘋果”得出相差數就是6,再根據相差數求移動數。大多數學生可能會“舍近求遠”選擇第一種做法。這就是一種思維慣性,即一定先求出另一個未知的量,兩個量都已知后,在圖上把兩個量都畫出來,在圖上找相差數確定移動數。從內部結構來分析,“移多補少”模型的建立分為兩個階段:第一階段是在實物圖感知經驗的基礎上建立的,在學生的頭腦中有著牢固的表象基礎,這種形象支撐讓學生更容易理解模型。第二階段是直接找“相差數和移動數之間的關系”從而確定移動數,是建立在第一階段基礎上的一種理論概括,更具抽象性。它不僅僅是知識層面的拓展,更是一個從形象到抽象的拓展。
所以例3.3存在的目的就是打破思維慣性,讓學生理解這個模型的本質是找到相差數從而確定移動數,如果相差數已知就不需要再去求相差數,這個“小插曲”能使學生建立的模型更加完善,對模型的理解也更透徹深入。
(四)逆向而行,固模型
逆向思維也叫“求異思維”,可以想成“反其道而思之”,讓思維向對立面發展,從問題的相反面深入探索,進一步完善知識結構。如對例1進行逆向思考,形成可逆關系的一組題。
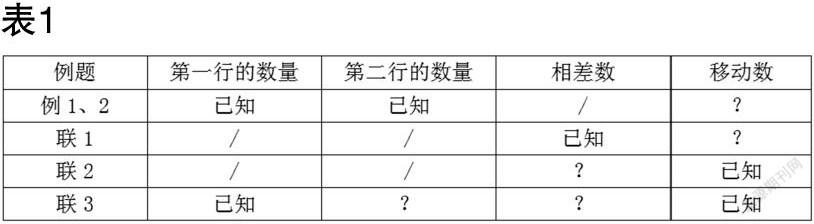
聯1:要使上面一行比下面一行的鉛筆多4支,可以怎么移?
聯2:上面一行的鉛筆移2支到下面一行后,兩行的鉛筆就同樣多,原來上面一行比下面一行多幾支?
聯3:按要求擺一擺,畫一畫。要求:從第一行移動2個○到第二行,兩行就同樣多。
以上題組的內部結構分析如表1所示,聯1是將例1、2的條件作等價變換,結構是和例題一致的,聯2是例題的逆向結構,即已知移動數反過來求相差數,聯3則是在聯2的基礎上的深化,已知移動數求相差數后,再根據相差數和其中一個量求另一個量。正向和逆向的雙向思考,可以使該類型的內部結構清晰明了,更有助于學生建立認知網絡結構,鞏固模型。
三、多維拓展:促生長
(一)橫向而行,拓寬度
1. 拓“對象”,由二元到多元
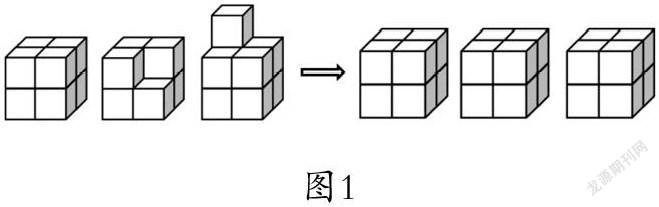
例4.1圖1中一共有多少個小正方體?
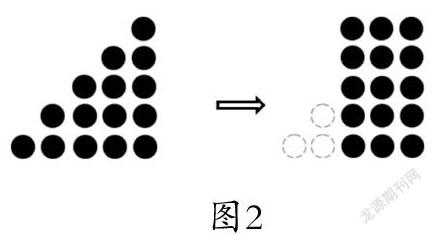
例4.2 圖2中一共有多少個棋子?
例4.3 一分鐘內,三個學生跳繩分別為80、75、85下,可以把這三個學生的成績都看成1分鐘()下。
例4.4 把下列加法算式改寫成加數相同的加法算式。
①4+5+6=? ? ? ? ? ? ? ? ? ②4+5+6+7+8=
①與原例題相比,對象拓寬,從2個增加到3個,但是解決問題的模型沒變,仍然是找相差數后求移動數,但是思維難度加深
2.拓“解法”,由單一到多種
例5 兔哥哥采了6個蘑菇,兔弟弟采了4個蘑菇,兔媽媽把她采的10個蘑菇分給兔哥哥和兔弟弟,怎么分,兩人擁有的蘑菇同樣多?
這題可以用“移多補少”的方法,先將兔弟弟比兔哥哥少的2個蘑菇補齊,然后將剩下的蘑菇平均分,還可以將三人的蘑菇合起來,再平均分成兩份分給兔哥哥和兔弟弟。一題多解能開闊學生視野,豐富學生的解題思路。
(二)縱向而行,拓深度
縱向對問題進行深度上的拓展,即對原問題進行半等價變化,如加強或減弱原問題的條件,可得到原命題的抽象或弱抽象命題,這就是一種半等價變化。
例6.1 哥哥比妹妹多9張郵票,哥哥給妹妹幾張后,還比妹妹多3張?
例6.2 哥哥比妹妹多9張郵票,哥哥給妹妹幾張后,哥哥反而比妹妹少3張?
例6.3 哥哥給妹妹5張郵票后,哥哥還比妹妹多2張,原來哥哥比妹妹多幾張郵票?
例6.4 哥哥給妹妹5張郵票后,哥哥還比妹妹少2張,原來哥哥比妹妹多幾張郵票?
這組例題在原例題的基礎上,將問題從“同樣多”變更為“還比妹妹多3張”,再將“多3張”變更為“少3張”,將問題半等價化拓展深度,通過對比尋“變”,而尋“變”過程中知“不變”,通過多維延伸拓展探尋出“不變”的本質。而例6.3和例6.4則是從逆向角度,同樣將問題半等價化拓寬深度,再次在“變”中探尋到“不變”的本質特征,也算從另一個方向驗證結果,正向和逆向雙向貫通,更能加深學生對知識內部結構的深度理解。
總之,在編寫拓展性學材時,教師應注重讓學生經歷學習序列,感受建模之路,促進學生知識和能力的生長。
參考文獻:
[1]喻平.數學教學心理學[M].北京:北京師范大學出版社,2018.
[2]孔凡哲.數學學習心理學[M].北京:北京大學出版社,2012.
(作者單位:浙江省玉環市城北學校)

