拓展驗證方法　學會理性思考

孫保華

【摘? ?要】當學生憑借數學的直覺思維提出各種猜想后，教師應該引導他們小心求證。不僅要讓他們猜想“是什么”，更要引導他們驗證“為什么”。因此在教學中教師要讓學生合理提出猜想，突出驗證的環節，并根據不同的知識類型，尋求多種驗證方法，學會理性思考。

【關鍵詞】拓展;驗證;方法;理性;思考

荷蘭數學教育家弗賴登塔爾說：“真正的數學家常常憑借數學的直覺思維做出各種猜想，然后加以證實。”因此，教師要鼓勵學生提出猜想并積極驗證，增強主動探究、獲取數學知識的能力，促進學生創新思維的發展。在實際教學中，教師要根據學生的年齡特點和活動經驗嘗試從不同的角度，拓展驗證的方法，培養學生嚴謹的思維方式。

一、片面與全面——取長補短

小學數學中有歸納數學規律的學習。教學中，教師通常會先呈現幾個具體例子讓學生進行猜想，再讓學生自主舉幾個例子來驗證。如果學生舉的例子可能導致得出錯誤的結論，那么教師有必要對這種枚舉驗證進行優化。在枚舉驗證時，要考慮的不在于例子的個數，而在于例子的類型。因此在教學中，教師要引導學生全面地思考問題，驗證時要從多種類型、多個角度來舉例子，說明猜想的正確性。請看以下教學片段。

在教學完乘法口訣后，教師出示如下三組不等式。

3×7>3+7? ? ?3×8>3+8? ? 3×9>3+9

師：請同學們仔細觀察這三組不等式，你有什么發現？

生：我發現3×7的積21大于3+7的和10。

生：我發現3×9的積27大于3+9的和12。

生：從這三個不等式中我發現兩個數的乘積大于這兩個數的和。

師：大家都有一雙會發現的眼睛。是的，在這兒兩數之積大于這兩個數之和。請大家再舉例驗證一下。

生：5×6>5+6，5×7>5+7，5×8>5+8。

生：4×5>4+5，4×8>4+8，4×9>4+9。

……

很多教師一般教學到此為止，不再引導學生繼續思考。這里學生舉的例子只是一些同類型的不等式，那么其他有關的不等式是否也有這樣的規律呢？因此在學生枚舉驗證時，教師要及時進行引導與糾正，要強調例子的類型，而不只是盲目地舉例。

師：這個猜想正確嗎？這里只是列舉了一些同類型的不等式。同學們可以再舉一些與特殊數相關的不等式，如與0、1、2有關的不等式來驗證我們提出的猜想。

生：0×7<0+7，0×9<0+9，0×6<0+6，我發現與0有關的不等式兩數之積小于兩數之和，與我們剛才的猜想正好相反。

生：1×5<1+5，1×7<1+7，1×8<1+8，我發現與1有關的不等式兩數之積小于兩數之和，與我們剛才的猜想也正好相反。

生：2×1<2+1，2×2=2+2，2×3>2+3，2×4>2+4……我發現與2有關的不等式，另一個乘數等于1時兩數之積小于兩數之和，另一個乘數等于2時兩數之積與兩數之和相等，另一個乘數是3時兩數之積大于兩數之和。

師：通過進一步舉例，你們認為我們剛才的猜想還正確嗎？看來，舉例子驗證的時候，要找不同類型的例子。

當學生只舉出一些同類型的例子時，教師要及時進行點撥，引導學生發現規律。如當學生舉出與0、1有關的不等式時，發現的規律與之前的猜想正好相反;當學生舉出與2有關的不等式時，發現有三種不同的情況。通過這樣的教學活動，學生發現舉例需要全面考慮，要舉出不同的類型，甚至發現只要舉出一個反例就能推翻之前的猜想。

二、枚舉與推理——相輔相成

在枚舉驗證過程中，教師要引導學生全面地思考問題，要從多種類型、多個角度來進行分類舉例，同時所舉的例子要具有一定的代表性和典型性。如此仍不能保證前期的猜想一定是正確的。因此教師可以引領學生向推理驗證轉變，讓學生經歷推理過程，進一步來驗證猜想的可靠性，提升學生思維的深刻性。

例如，蘇教版教材四年級下冊“加法交換律和結合律”的教學。

生：交換兩個加數的位置，和不變。

師：這只是一個猜想，那么這個猜想到底對不對呢？還需要我們進一步驗證。你們認為可以怎樣進行驗證？

生：再舉一些例子，看是不是都符合“交換兩個加數的位置，和不變”的規律。

師：請同學們在研究單上再寫三個這樣的等式。想一想這樣的等式有怎樣的規律。

生：3+5=5+3，24+27=27+24，126+213=213+126。

生：0+15=15+0，13+1=1+13，1+0=0+1。

生：0.6+0.2=0.2+0.6，0.3+0.5=0.5+0.3，0.4+0.3=0.3+0.4。

生：2/7+3/7=3/7+2/7，2/5+1/5=1/5+2/5，1/3+2/3=2/3+1/3。

……

生：我發現不管是整數，還是小數和分數，交換兩個加數的位置，它們的和都不變。

師：瞧，這些同學舉的例子可真豐富，有整數的例子，有小數和分數的例子，還有與0有關的例子，它們相加的和都不變。這樣的例子能列舉得完嗎？

生：不能。

師：有哪位同學找到交換兩個加數的位置之后和不相等的例子嗎？

生：沒有。

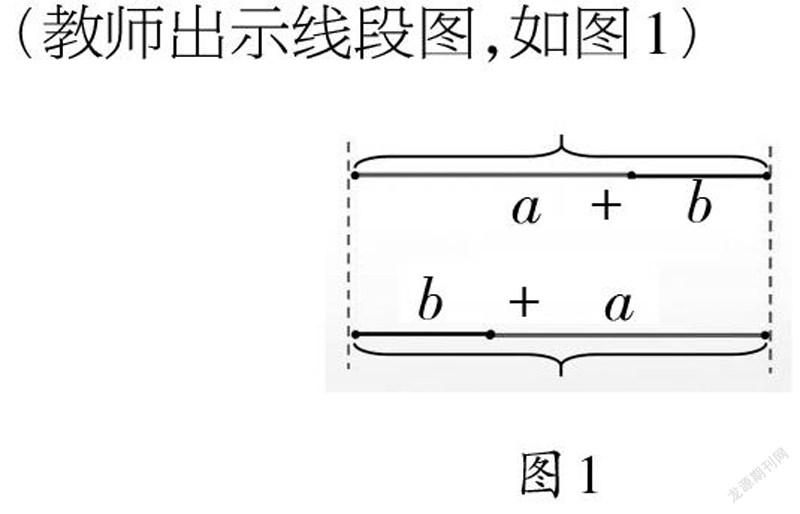
師：同學們舉的例子各不相同，但得到的規律是一致的。其實，我們也可以用線段圖來表示加法交換律。

（教師出示線段圖，如圖1）

師：誰來說說示意圖表示的意思？

生：第一條長線段可以用a+b表示，交換a、b兩條線段的位置，第二條長線段可以表示為b+a。

生：交換位置以后這兩條長線段的總長度沒有變化。也就是交換兩個加數的位置，它們的和不變。

當學生提出猜想后，教師及時讓學生進行舉例驗證。學生舉出的例子有整數、小數和分數，還有與0有關的特殊例子，分類舉出一些例子且具有一定的代表性。同時學生舉不出反例。教師并沒有滿足于此，繼續引導學生用數形結合的方式進行推理驗證，這種從特殊例子到一般表達進一步確保了猜想的正確性，促進了學生思考問題的完整性。

三、操作與推理——相得益彰

雖然學生可以通過操作，在具體感知和直接觀察中驗證猜想，但測量、撕拼、折拼等操作實驗不可避免地會存在誤差，這是操作驗證的局限性。如何彌補這種局限性？教師應該尋求更嚴密更科學的驗證方法。可以把已知的對象進行轉化和推理，經歷從操作驗證到推理驗證的思維跨越，提升學生思維的縝密性和深刻性。

例如，蘇教版教材四年級下冊“三角形的內角和”的教學。

師：請同學們任選一個直角三角形，測量三個內角的度數，再算一算內角和是多少。

（學生進行測量并計算）

師：直角三角形的內角和是多少度？

生：直角三角形的內角和是180°。

師：有沒有不是180°的？

生：我量的這個三角形三個角的度數和是182°。

生：我量的這個三角形三個角的度數和是177°。

生：測量會出現誤差。

師：有同學提出把直角三角形的三個角取下來合在一起，可以怎樣操作呢？

生：把三角形的三個角撕下來可以拼成一個平角，也就是180°。（邊說邊操作）

師：三角形的三個內角可以拼成一個平角，說明這個直角三角形的內角和是180°。能不能不破壞原來的三角形，直接把三個角拼在一起呢？

生：我是沿著兩條邊的中點折第一個角，其他兩個角的頂點與第一個角的頂點重合，正好折成一個平角，也就是180°。

生：我這個折出來角與角之間有空隙，好像比一個平角大一些。

師：剛才我們采用的折拼的驗證方法可能存在誤差，有沒有更加嚴謹、巧妙的驗證方法呢？老師這里有一張長方形的紙，你能想到什么？

生：長方形對邊相等，四個角都是90°。

生：可以沿著長方形的對角線對折，分成兩個完全相同的直角三角形。

師：真會動腦筋，分成了兩個完全相同的直角三角形。現在同學們能不能根據長方形的內角和來證明直角三角形的內角和呢？

生：因為我們是把一個長方形平均分成了兩個完全相同的直角三角形，兩個直角三角形的內角和正好等于這個長方形的內角和，所以只要用90°×4÷2=180°就可以得到一個直角三角形的內角和。

師：看來通過推理也能驗證直角三角形的內角和是180°。

學生用量、撕、折、拼的方法探索直角三角形的內角和，這些驗證方法都是屬于操作層面的，存在著一定的誤差。因此教師可以引導學生尋求更加嚴謹的驗證方法，利用長方形的特征來推導直角三角形的內角和。通過這樣的推理驗證會使結論更具一般性和科學性。

四、抽象與形象——有機結合

在驗證環節，很多教師喜歡帶領學生用嚴密的演繹推理來驗證猜想。這些嚴密的演繹推理很多是全符號的，這樣的驗證雖然短小精悍但很抽象，學生不易接受。根據學生的年齡特點，教師可以對驗證過程進行改造，用“形象”化的演繹推理來驗證猜想。這一驗證過程將一些非本質的東西進行改造使其形象化，既保持了演繹推理中原本所蘊含的邏輯關系和相對嚴謹的思維過程，又讓學生充分理解了驗證過程，加深了對知識的理解。

例如，蘇教版教材五年級下冊《和與積的奇偶性》的教學。

師：奇數與奇數的和是奇數還是偶數？請同學們任意找兩個奇數，把它們相加，觀察結果說說你的發現。

生：我用3+5=8，7+9=16，5+7=12，發現兩個奇數相加的和是偶數。

生：我用111+213=324，123+17=140，23+13=36，同樣發現兩個奇數相加的和是偶數。

……

師：兩個奇數相加的和是偶數，這只是我們的一個猜想，如何來驗證這一猜想呢？

教師引領學生經歷嚴密的演繹推理，驗證過程如下。

證明：假設這兩個奇數分別是a=2k+1，b=2k+1，那么a+b=2k+1+2k+1=2k+2k+2=2（k+k+1），所以2（k+k+1）是一個偶數，即a加b的和是一個偶數。

這是一個嚴密的代數推理驗證，學生需要理解奇數與偶數的代數式，還要對用字母表示的代數式進行恒等變形，并通過變形后的代數式進行奇偶性判斷。這種符號化的代數推理很有數學味，但不符合小學生的認知水平。教師需要對驗證過程進行改造，將奇數與偶數的代數式表示進行直觀化，變成讓學生能充分理解的方式，將原本抽象的代數推理過程形象化。

奇數和偶數的代數式表示用圖形來直觀化，這種“形象”化的邏輯推理，大大降低了學生理解的難度，同時也能達成一個相對嚴謹的思維過程，更有利于培養學生的抽象思維能力。

真正的數學教學不僅只停留在通過歸納和類比得到猜想，更應該在驗證環節予以重視。如果猜想是學生數學思維發展的風帆，那驗證就是輕舟前行的雙槳，只有揚起風帆撐起雙槳，才能讓學生在數學的海洋中暢游。

參考文獻：

[1]汪培新.核心素養與小學數學[M].北京：科學出版社，2019.

[2]吳正憲，劉延革.發展兒童數學關鍵能力[M].北京：教育科學出版社，2017.

（江蘇省常州市金壇華城實驗小學? ?213200）