數學解題教學需從“就法論法”走向“以法生法”
——由一節高三復習課引發的思考

江蘇省南京市金陵中學河西分校 (210019) 楊 紅

高三復習課階段，解題教學就成為了課堂教學的“主旋律”.解題教學不能“就題論題”，而是要做到“歸一類、得一法、通一片”，但現實教學中，不少教師的教學有避免“就題論題”現象的想法，但“就法論法”的現象依然明顯.筆者最近聽了一節高三復習課，深有感觸.

1 教學過程簡介

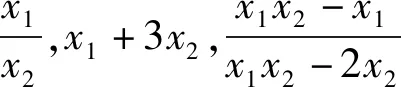
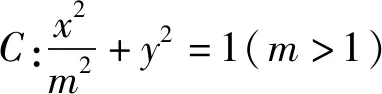
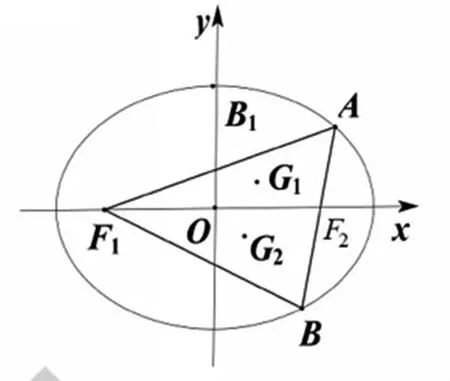
圖1

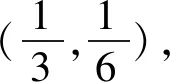
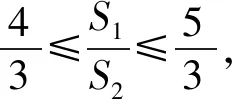
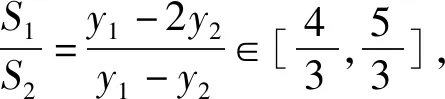
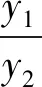
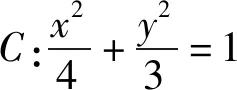
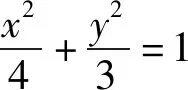
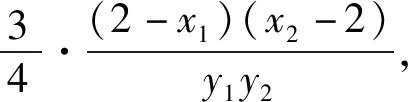
講完兩道例題后，接下去就是課堂練習，至此，本節課就結束了.縱觀整節課，雖然涉及的方法比較巧妙，但自始至終都是教師在講，學生沒有獨立思考的時間，完全是在“記憶、模仿”解題的結論和方法.

2 “就法論法”是一種急功近利的表現

課后，筆者就這節課的“師生互動”問題和上課教師進行了交流.上課教師給出的解釋是：經過二輪復習，學生已經掌握了相當多的解題技巧，因此，教師只要把方法告訴學生，學生就能夠理解與掌握，沒必要再花時間在“師生互動”上；再說本節課的方法比較巧妙，學生自己很難想到，直接把方法呈現出來，能夠提升教學效率.教師給出的解釋聽起來似乎有些道理，但仔細分析后，不難發現，這是一種“急功近利”表現，與學生的認知規律不相符.

2.1 “就法論法”以灌輸現成結論為目標

現在關于解題方法研究的成果很多.因此，“拿來主義”就成了很多教師的不二選擇，見到比較巧妙的解題方法，就直接照搬過來.由于好的方法實在太多，但教學時間有限，于是以“灌輸”代替生成，以強化訓練代替內化，就成為了高三解題教學的一種比較普遍現象.

本節課中“非對稱韋達定理”的應用技巧在圓錐曲線的運算中確實能起到化繁為簡的功效，但教師顯然“太急”，學生還沒理解題意，就給出了解題的過程，就把問題聚焦在對于目標函數的簡化上，使得教學過程被解題方法所“綁架”，純粹是為了灌輸方法而呈現方法，造成了方法與問題的分析、問題的解決過程相脫節.其實，教學的重心首先應該放在對解題思路的剖析上，自然得到目標函數后，再引導學生思考如何對目標函數進行化簡，這才是解題教學的正常流程.

2.2 “就法論法”無視方法之間的聯系

學生知識的獲得并不是靠教師的灌輸，而是在已有認知經驗下的意義建構，解題方法的獲得也是如此，它也是在學生已有解題經驗下的意義建構，但“就法論法”顯然忽視這一真相.“非對稱韋達定理”根基就是“韋達定理”，當遇到“非對稱”結構時，韋達定理雖然不能直接套用，但并不一定非要把“非對稱”化為“對稱”不可，直接運用“求根公式”把坐標表示出來也能解決問題，而用坐標直接表示屬于通性通法的范疇，是學生能夠想到的方法.在此基礎上，教師再引導學生思考如何對方法進行優化，從而自然引出如何把“非對稱”化為“對稱”，這樣通性通法與“巧法”之間就建立了聯系，學生也更容易理解數學方法的精髓了.

3 從“就法論法”走向“以法生法”

數學解題教學的真正目的并不是直接傳授新的方法，而是在通性通法的基礎上，通過思維的遷移，進一步優化生成更多“新”的方法.也就是說，解題教學的重心應該從“就法論法”向“以法生法”轉變，從而使得解題方法前后關聯，聯系緊密，形成完整的思維脈絡.下面以例2為例，談談具體的操作.

3.1 立足已有方法

3.2 生成創新解法

除了“消參”外，還可利用一些圓錐曲線的性質，實現“優法”.

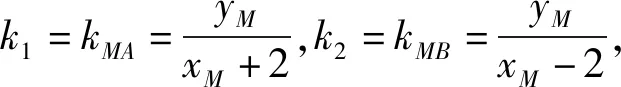
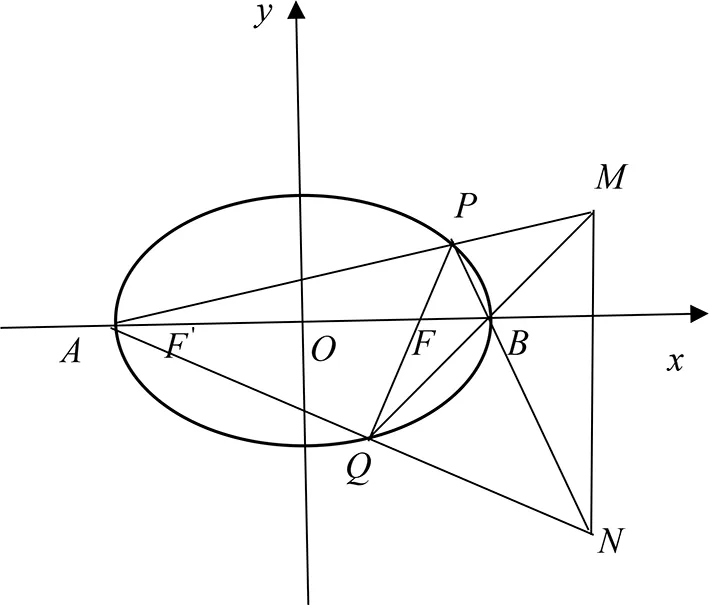
圖2

總之，數學解題方法并不是空穴來風，也不是無源之水無本之木，而是立足學生的已有經驗；數學解題教學也不是“灌輸”，而是靠學生主動的意義建構.解題教學不能被眼花繚亂的方法所左右，而是要透過方法看清背后的數學本質.