基于OBE理念的問題驅動教學改革與實踐
——以數據結構進階課程為例

柳 欣 李保田 薛玉利 唐 艷

1.山東青年政治學院信息工程學院，山東 濟南 250103

2.山東省高校信息安全與智能控制重點實驗室（山東青年政治學院），山東 濟南 250103

數據結構進階課程是我校計算機科學與技術專業的專業選修課。該課程對先修課程數據結構和算法設計與分析的教學內容進行了補充，同時對這兩門課程的重點內容進行了知識歸納和算法設計的思維拓展，形成了完整的數據結構與算法知識鏈。通過本課程的學習，學生能深入理解典型數據結構的重要性質、存儲結構以及具體實現，掌握重點算法，并能運用數據結構技術和算法設計策略分析、解決現實應用中的問題，培養軟件開發素質、工程意識和職業道德規范。數據結構進階課程的教學內容中包含大量復雜算法，這些算法具有存儲結構定義復雜、算法執行過程抽象、實驗難度大等特點，在傳統教學模式下，教師往往會面臨“教師講不動、學生沒興趣”的雙重困境。

一、支撐的教學理論

問題驅動教學是一種“以學生為主體、以問題為核心”的教學方法，其特點如下：（1）教師將教學內容嵌入精心創設的問題情境中，將課堂教學轉換為不斷地提出問題和解決問題的迭代過程。（2）強調學生是學習主體，是知識的主動探究者。教師的角色是組織和引導對問題的討論，并且為學生提供必要的幫助。（3）教學目標不是靠教師講授直接達成的，而是在教師與學生的共同努力下以遞進方式達成的，具體表現為認識問題，探索解決關鍵問題的途徑，逐步求精地解決問題，對不同的問題解決方法進行比較以及通過思考發散性問題實現知識拓展。成果導向教育（OBE,Outcomes-based Edu‐cation）是工程教育專業認證的核心理念，它強調首先明確學生的學習成果（即畢業要求），然后根據畢業要求對課程的教學目標和教學內容進行反向設計。思維可視化是一種利用圖像、媒介、言語和肢體表征對不可見的思維進行直觀展示的技術。該技術的成功運用可以加強學生的思維訓練，提升他們的創新思維層次。

二、問題驅動教學改革總體思路

（一）OBE理念下的教學目標制訂

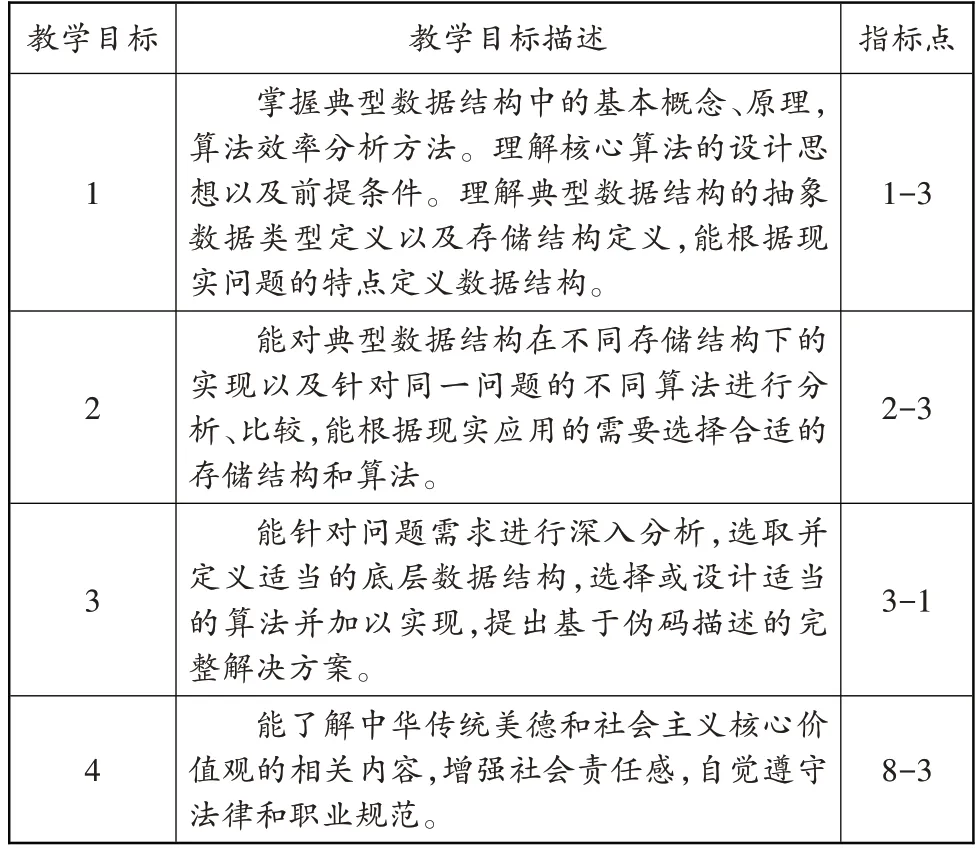
根據工程教育認證標準，我們將人才培養方案中的畢業要求細化為33 個二級指標點。數據結構進階課程對其中的4 個指標點形成支撐（如表1 所示），分別側重對學生的應用能力、分析能力、設計能力和職業規范進行培養。

在確定這些指標點之后，我們設置了4 個與之相應的教學目標（如表2所示）。

（二）案例算法選取

在教學目標確定之后，我們遴選了一部分有代表性的復雜算法作為實施問題驅動教學的內容。具體遴選原則如下：1.算法的底層存儲結構具有代表性，學習該算法有助于學生加深對順序/鏈式存儲結構的理解。2.算法的設計思想體現了典型的算法設計策略，能較好地對數據結構進階課程和先修課程算法設計與分析的教學內容進行銜接。3.算法有著較為廣泛的現實應用，有利于與思政元素進行結合。

（三）教學難點分析以及應對策略

在選定教學內容之后，我們結合教材中的算法描述，對有可能給學生理解造成障礙的關鍵點進行分析。以模式匹配算法為例，教材中介紹了兩個算法，即BF（Brute Force）的模式匹配算法和KMP（Kruth-Morris-Pratt）模式匹配算法。這兩個算法都采用了順序存儲結構，其核心思想是借助游標i 和j 對主串S 和模式T 中參與匹配的當前字符進行比較。通過分析發現，在教學過程中存在以下的難點：（1）當發生“失配”時，如何對游標i進行回溯。（2）在BF模式匹配算法中，利用語句“i=i-j+2;”實現對游標i的回溯，但是這條語句的可讀性欠佳。（3）教材的KMP算法描述中對“S[i]=T[j]”和“j=0”兩種情況下的游標設置進行了合并，致使理解算法的難度增大。

針對教學難點，我們采取了以下的應對策略：（1）在許多復雜算法中，都是先對特定條件做出判斷，然后分情況進行處理。對這些情況進行圖解，可以為學生自主探究提供最有效的學習“支架”。（2）教材中的算法描述往往是最精簡的形式，缺點是容易造成閱讀和理解的困難。對此，可以采用問題驅動教學方法，先引導學生將精力放在如何解決問題上，在歸納得出算法描述之后，再對算法描述進行化簡，最終得出與教材相同的算法描述。

（四）OBE 理念指導下的問題設計與問題驅動教學詳細設計

針對教學難點，我們在OBE理念指導下進行問題設計。教師將在問題驅動教學過程的不同階段提出這些問題，既能實現問題的抽絲剝繭、逐步求精，又能對人才培養方案中有關能力培養和職業規范的指標點進行支撐。以模式匹配算法為例，我們針對教學內容設置了10個具體問題（如表3所示）。

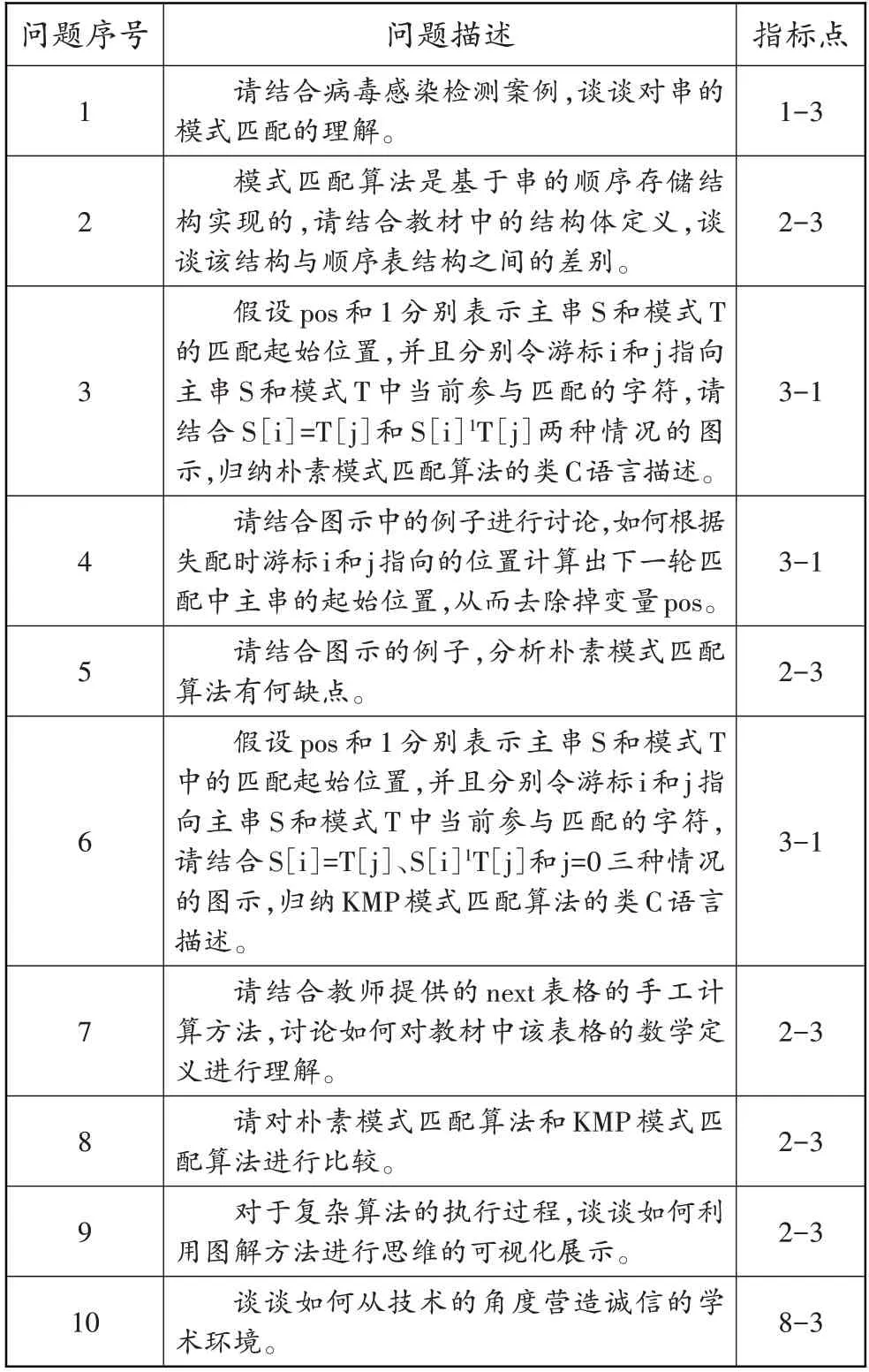
在完成問題設計之后，需要圍繞這些問題開展問題驅動教學的詳細設計。在該過程中，我們采用文獻［3］的做法，將每個階段的教學過程劃分為多個循序漸進的板塊，即問題情境、自主探究、合作交流、總結提升和遷移拓展。

三、問題驅動教學設計舉例

我們以模式匹配算法為例，給出一個具體的問題驅動教學的教學設計案例（教師提出的問題均來自表3）。本次課的教學目標如下：（1）理解字符串的順序存儲結構、掌握BF 模式匹配算法和KMP 模式匹配算法。（2）通過課程思政使學生了解社會主義核心價值觀倡導的誠信理念，保持科研誠信、杜絕抄襲行為。考慮到KMP 算法是在BF 算法基礎上改進得到的，我們將整個教學過程分為以下兩個階段。

（一）第一階段——樸素模式匹配算法的問題驅動教學

問題情境板塊：教師介紹教材中的病毒感染檢測案例，并且提出問題1。

自主探究板塊：首先，教師簡要回顧字符串順序存儲結構，并且提出問題2。接下來，教師提供對模式匹配問題的完整描述以及重要的符號定義。最后，教師向學生提供有關算法匹配過程中“成功”和“失配”兩種情況下的圖示（如圖1所示，匹配成功的區域用灰色填充），并且提出問題3。該板塊結束后，學生會在教師提示下自行寫出算法描述。

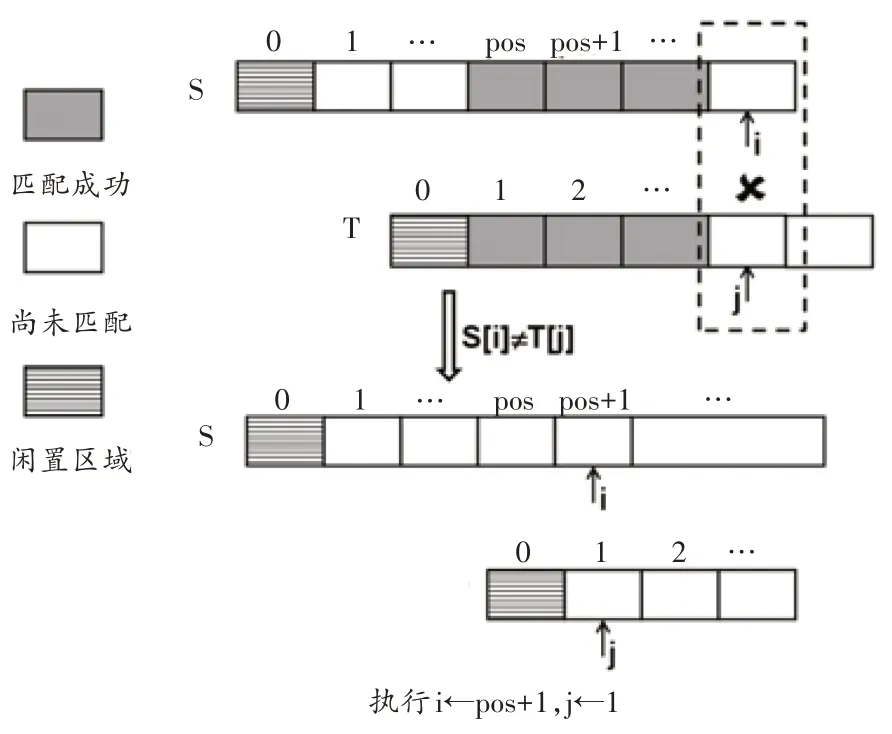
合作交流板塊：教師要求學生以小組為單位將寫出的算法描述與教材中的算法描述進行對照。容易發現，兩者并不一致。這主要體現在，當發生失配時，教材并未使用語句“i=pos+1;”對游標i進行回溯，而是使用了令人費解的語句“i=i-j+2;”。對此，教師提出問題4，并且為學生提供一個具體的例子作為學習支架（見圖2）。通過討論，學生終于理解如果將回溯位置pos+1 視為未知數，同時將i 和j 的當前位置視為已知數，則可以通過解方程而求出pos+1的值，即i-j+2。

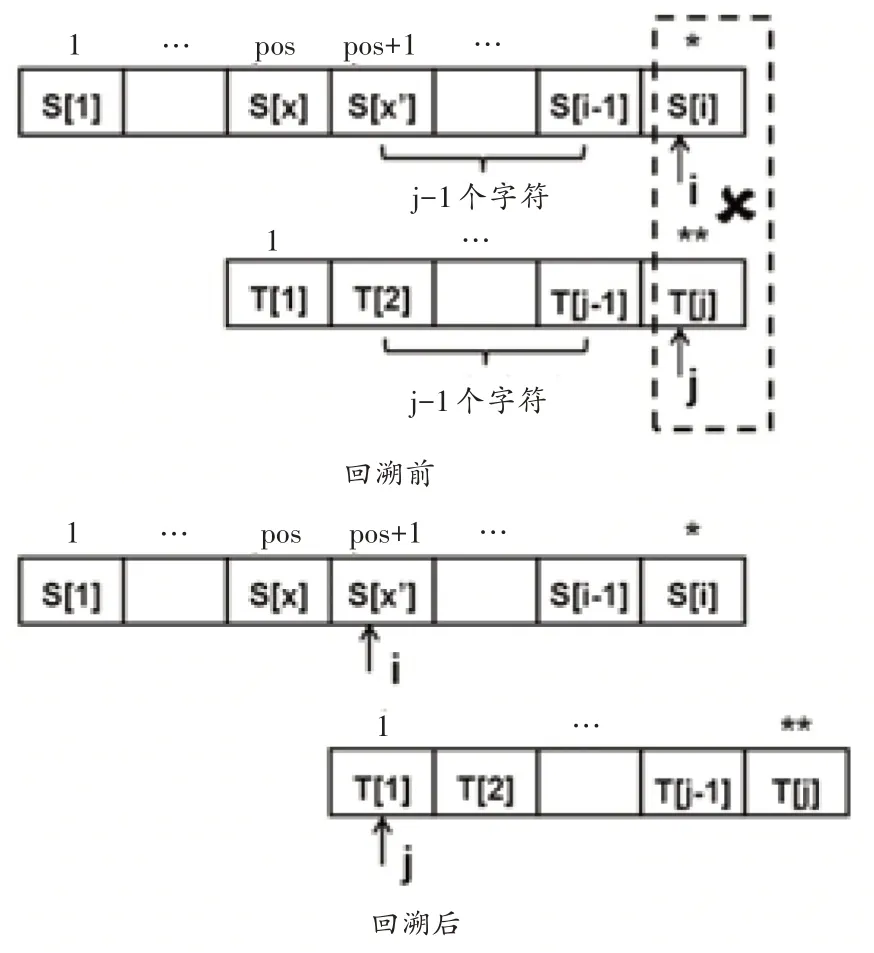
總結提升板塊：為了鞏固學習成果，教師向學生提供文獻［8］中的模式匹配問題實例S="ababcabcacbab"，T="abcac"，并且要求學生利用圖解方法進行模式匹配，且主串S的匹配開始位置為i=3。這是一個精心設計的“陷阱”，學生需要總共執行4 輪模式匹配（即當主串的匹配起始位置為i=6時）才能最終取得匹配成功。此時，學生發覺算法的回溯策略并非總是有效的，存在即使執行回溯也會“做無用功”的現象。此時，教師可以提出問題5。

（二）第二階段——KMP 模式匹配算法的問題驅動教學

問題情境板塊：教師介紹KMP 算法，并且指出該算法可以有效地避免上述“做無用功”的現象。同時，強調該算法假設存在一個“神奇”的next表格。

自主探究板塊：教師將KMP算法每輪的匹配過程分為“本輪匹配成功”“本輪發生失配”和“上一輪發生失配導致j 回退到0”三種情況，并且利用思維可視化技術為學生提供圖形化的學習支架，如圖3所示，匹配成功的區域用灰色填充。最后，教師提出問題6。

合作交流板塊：教師強調，盡管已經理解了KMP 算法的核心技術，但是必須將next 表格構造出來，否則KMP算法就是“無源之水，無本之木”。在具體教學過程中，教師首先介紹用于構造next表格的手工算法，然后提出問題7。

總結提升板塊：在該板塊，教師提出問題8，并且以討論的形式對兩個算法進行優缺點比較。教師負責引導討論的走向，最終得出以下結論：（1）KMP算法適合于從外存中讀取主串的情況。（2）KMP 算法并非總是優于BF算法。

遷移拓展板塊：教師強調學習數據結構最大的困難在于理解和設計算法。選取適當的例子進行圖解分析，不但可以降低問題難度，而且有助于歸納得出算法描述中的關鍵語句。此時，教師提出問題9，鼓勵學生將圖解作為攻克復雜算法的“利器”。事實上，模式匹配算法是設計論文抄襲檢測算法的重要基礎。我們認為，這個思政元素與教學內容緊密結合，容易為學生所接受。因此，教師可以不失時機地介紹這個應用，并且提出問題10，使學生明確恪守職業道德、堅守學術誠信與社會主義核心價值觀倡導的誠信理念在本質上是一致的。

四、滿意度調查

為了了解問題驅動教學改革的實際效果，我們在結課后利用“問卷星”向學生發布了匿名調查問卷。問卷內容主要涉及課程教學滿意度、問題驅動教學法對學習積極性的促進作用、對問題的難度評價、圖解是否有助于對算法關鍵執行過程的理解、是否希望教師提供有針對性的圖解作為學習支架等內容。

結果顯示，有68.64%的學生認為問題驅動教學有助于提高學習積極性，有85.59%的學生贊同教師提供圖解作為學習支架的做法。這說明該嘗試取得了較好的效果。

五、結束語

為了改善數據結構進階課程的教學效果，本文提出了基于OBE 理念的問題驅動教學改革思路。通過引入OBE 理念，使得課程教學目標聚焦于對學生的應用能力、分析能力、設計能力和職業規范的培養。同時，教師必須在問題設計階段充分考慮教學內容對指標點的有效支撐。此外，以模式匹配算法為例，提出詳細的問題驅動教學設計案例。今后，我們將在以下方面繼續深化現有研究：（1）建立面向數據結構進階課程的問題驅動教學案例庫。（2）在OBE理念指導下，開展針對問題驅動教學內容的知識點考核達成度評價，根據評價結果改善教學方法和內容，形成“問題驅動教學—達成度評價—改進教學”的完整閉環結構。